题目描述：

在由 1 x 1 方格组成的 n x n 网格 grid 中，每个 1 x 1 方块由 '/'、'\' 或空格构成。这些字符会将方块划分为一些共边的区域。

给定网格 grid 表示为一个字符串数组，返回 区域的数量 。

请注意，反斜杠字符是转义的，因此 '\' 用 '\\' 表示。

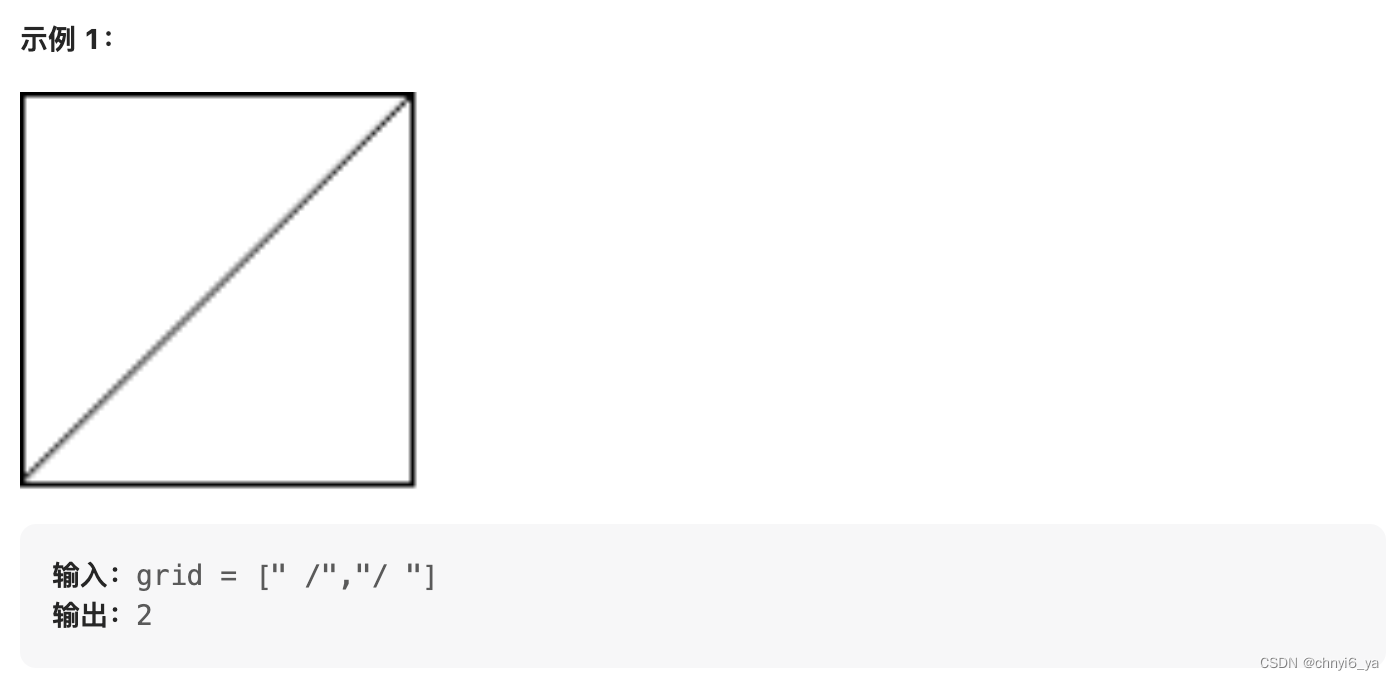
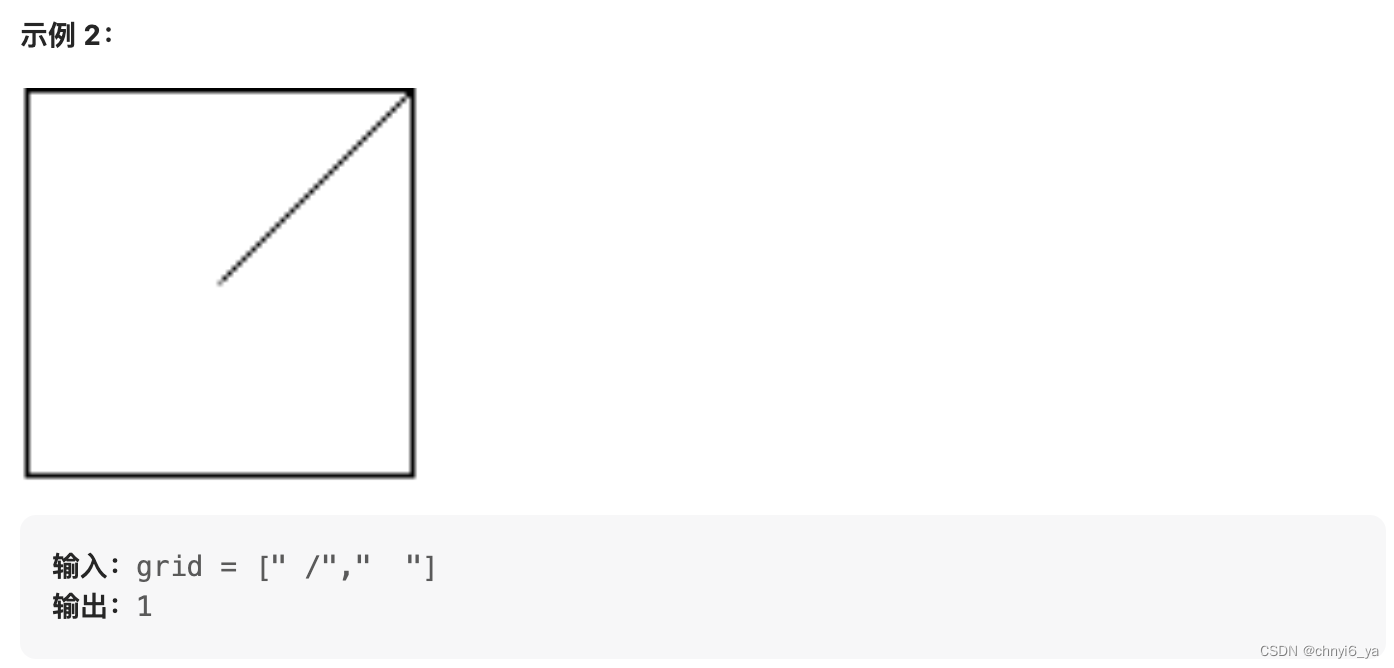
这题我看了一个题解，就是把每一个1x1的小方格还要分成上下左右四个三角形块，给这些三角形编上编号后，通过并查集，把需要合并的块变成连通块，最后计算连通块的个数，也就是区域个数。

具体代码如下：

class Solution {
public:
    int Find(vector<int>& f,int x){
        if(f[x] != x){
            f[x] = Find(f,f[x]);
        }
        return f[x];
    }

    void Union(vector<int>& f,int index1,int index2){
        f[Find(f, index1)] = Find(f, index2);
    }

    int regionsBySlashes(vector<string>& grid) {
        int n = grid.size();
        vector<int> f(n*n*4);
        for(int i = 0;i<n*n*4;i++){
            f[i] = i;
        }
		
		// 假设n=2，那么大的方格按左上角、右上角、左下角、右下角分成四个小方格，
		// 这四个小方格的idx分别是 0、1、2、3
        for(int i = 0;i<n;i++){
            for(int j = 0;j<n;j++){
                int idx = i*n+j;
                if(i<n-1){
                	// 无论是‘/’还是‘\\'，一个小方格中最底下的三角形
                	//和挨在下面的小方格的最上面的三角形一定是会合并在一起的
                    int bottom = idx + n;
                    Union(f, idx*4+2, bottom*4);
                }
                if(j<n-1){
                	// 同理，无论是‘/’还是‘\\'，一个小方格中最右边的三角形
                	//和挨在右边的小方格的最左边的三角形一定是会合并在一起的
                    int right = idx+1;
                    Union(f, idx*4+1, right*4+3);
                }
                // 其余的小三角形块是否合并就根据 左斜杠、右斜杠、空格来决定 
                if(grid[i][j] == '/'){
                    Union(f, idx*4, idx*4+3);
                    Union(f, idx*4+1, idx*4+2);
                }else if(grid[i][j] == '\\'){
                    Union(f, idx*4, idx*4+1);
                    Union(f, idx*4+2, idx*4+3);
                }else {
                    Union(f, idx*4, idx*4+1);
                    Union(f, idx*4+1, idx*4+2);
                    Union(f, idx*4+2, idx*4+3);
                }
            }
        }

        int count = 0;
        for(int i = 0;i<n*n*4;i++){
            if(f[i]==i) count++;
        }

        return count;
    }
};