题目一

给定一个整型数组arr，和一个整数num某个arr中的子数组sub，如果想达标，必须满足：sub中最大值-sub中最小值<=num，返回arr中达标子数组的数量

滑动窗口法,滑动窗口有两个行为1.右括 2.左缩

错误想法1:

当你已经维持住了一个窗口 假如说目前这个窗口中的最大值-最小值已经满足条件 那么就可以"左缩" (实际上呢 就是换一个开头 实际上是枚举每一个开头的结果) 如果这个窗口不满足条件 那就要右扩一个格子 看看新加进来的这个数能不能对结果产生影响 如果满足了 左缩 不满足接着右扩 每次满足都累计一次结果

这样的话就只需要遍历一次数组就可以了 不需要大量枚举每一个子数组了

错在哪了呢: 就是按照这个逻辑 当这个数组成立的时候 你不能立刻切换开头 因为你新加一个数 还可能对它造成影响 也可能满足 所以你也要右扩 只有把所有以i开头的都遍历完了 才能左缩一个格子

如果arr[]达标 那它的子数组也一定达标

如果arr[]不达标 那它往左扩往右扩一定不达标

这么一听是不是挺扯的?新加一个数或者减少一个数一定没有影响

我们来分析一下 一个窗口里面 最大值为5 最小值是1  目标值是3 它目前不达标对吧 我们新加一个

数进来 如果你不大于也不小于 原本的最大值最小值 那你压根改变不了最大值最小值的结果 如果你比最大值大或者比最大值小 哎 你让之前的结果变得更大了 更不满足了

那么 最大值为4 最小值为3 目标值是2 呢? 它目前达标对吧 我们删掉一个值 假如说删的不是最大值最小值 哎 没影响 如果是最大值最小值呢 那么留下的新最大值最小值 一定比之前的最大值最小值还小

按照这个逻辑呢 我们可以直观的认为 扩大窗口可能会导致最大值减最小值变大 但绝不可能变小

缩小窗口会导致最大值减最小值变小 而不可能变大

错误想法2:

我们满足这个条件的时候 就可以让最大值减最小值变大一点 看看能不能成立 不满足这个条件呢 就变小一点 看看能不能成立 找到这个满足条件最大的窗口 就是最终结果吗? 他不是有序数组 不是连着的 可能会有两个独立的窗口(不同的元素为头) 所以说 我们的R走到头之后 还要看L走没走到头(另一个元素为头) 

错误想法3:

决定如果满足R走 不满足L走 当L>R的时候RL一起走 然后当每次满足之后的第一次不满足 就收集结果 它的所有子数组都是结果 这样就导致了 有很多重复的结果 需要去重 这就很难判断 

也就是说我们不能用 右扩左缩的方式 想象这么一种情况 我们一下子直接把R干到底 这时候L还在最开始的位置 这个时候我们累计的结果都是以0位置开头的 那1位置 2位置的子数组呢? 对吧 这很明显是缺的

错误4:所以直接 每次R走到头 L走一步再让R走到头 我们之前给的优化条件没用上(矫枉过正 虽然这样收集稳定了 但是和暴力解复杂度是一致的)

如果arr[]达标 那它的子数组也一定达标

如果arr[]不达标 那它往左扩往右扩一定不达标

R走到这个位置了 再往下走走不动了 这时候收集一份以L 开头的答案 然后L再往后走 收集L+1开头的答案 这样就可以不重复的收集所有答案了  然后呢 这次面对错误2的解法是怎么修正的呢 在R走不动之后 L继续走 L一直会走过R 从这时候开始 就获得了新生 它不再是之前的子数组了 他可以收集这个数组上所有的答案 本质上来讲 只是错误三的收集答案有改动 不要一起全部收集 要L一步一步往前走的收集 这样就不会有太多的if语句

public static int getNum1(int[] arr, int num) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		LinkedList<Integer> qmin = new LinkedList<Integer>();
		LinkedList<Integer> qmax = new LinkedList<Integer>();
		int L = 0;
		int R = 0;
		// [L..R) -> [0,0) 窗口内无数 [1,1)
		// [0,1) -> [0~0]
		int res = 0;
		while (L < arr.length) { // L是开头位置，尝试每一个开头

			// 如果此时窗口的开头是L,下面的while工作:R向右扩到违规为止

			while (R < arr.length) { // R是最后一个达标位置的再下一个
				while (!qmin.isEmpty() && arr[qmin.peekLast()] >= arr[R]) {
					qmin.pollLast();
				}
				qmin.addLast(R);
				// R -> arr[R],
				while (!qmax.isEmpty() && arr[qmax.peekLast()] <= arr[R]) {
					qmax.pollLast();
				}
				qmax.addLast(R);

				if (arr[qmax.getFirst()] - arr[qmin.getFirst()] > num) {
					break;
				}
				R++;
			}

			// R是最后一个达标位置的再下一个，第一个违规的位置
			res += R - L;

			if (qmin.peekFirst() == L) {
				qmin.pollFirst();
			}
			if (qmax.peekFirst() == L) {
				qmax.pollFirst();//到这知道为啥不能简单的维护max和min值了 你弹出去的不知道是哪个 想找第二大的还要遍历
			}

			L++;

		}
		return res;
	}

题目二

KMP算法

首先 我们先了解一下 KMP算法的作用 str1 和str2 字符串 如果str1中包含str2 那么返回头位置

如果不包含返回-1

首先 我们先加入一个概念: 有一个next数组 next[i]的值为 str2 中 以i-1位置为结尾的字符串中 最长相同前缀后缀为多长(相同前缀后缀 不是对称  aba 中相等的后缀为a 而非ab ba(这个是对称) 且不要让前缀\后缀长度等于字符串  因为对于任何一个字符串来说 它本身的最长前缀/后缀都是它本身 肯定相等)

举个例子 a b a b f f位置的next值为2   0 1 位置的next值恒为-1

好 来开下流程 str2先匹配str1 两个指针齐头并进 到达第一个不满足的位置 它位置的next值为5 那么直接从str2的5位置接着匹配下去

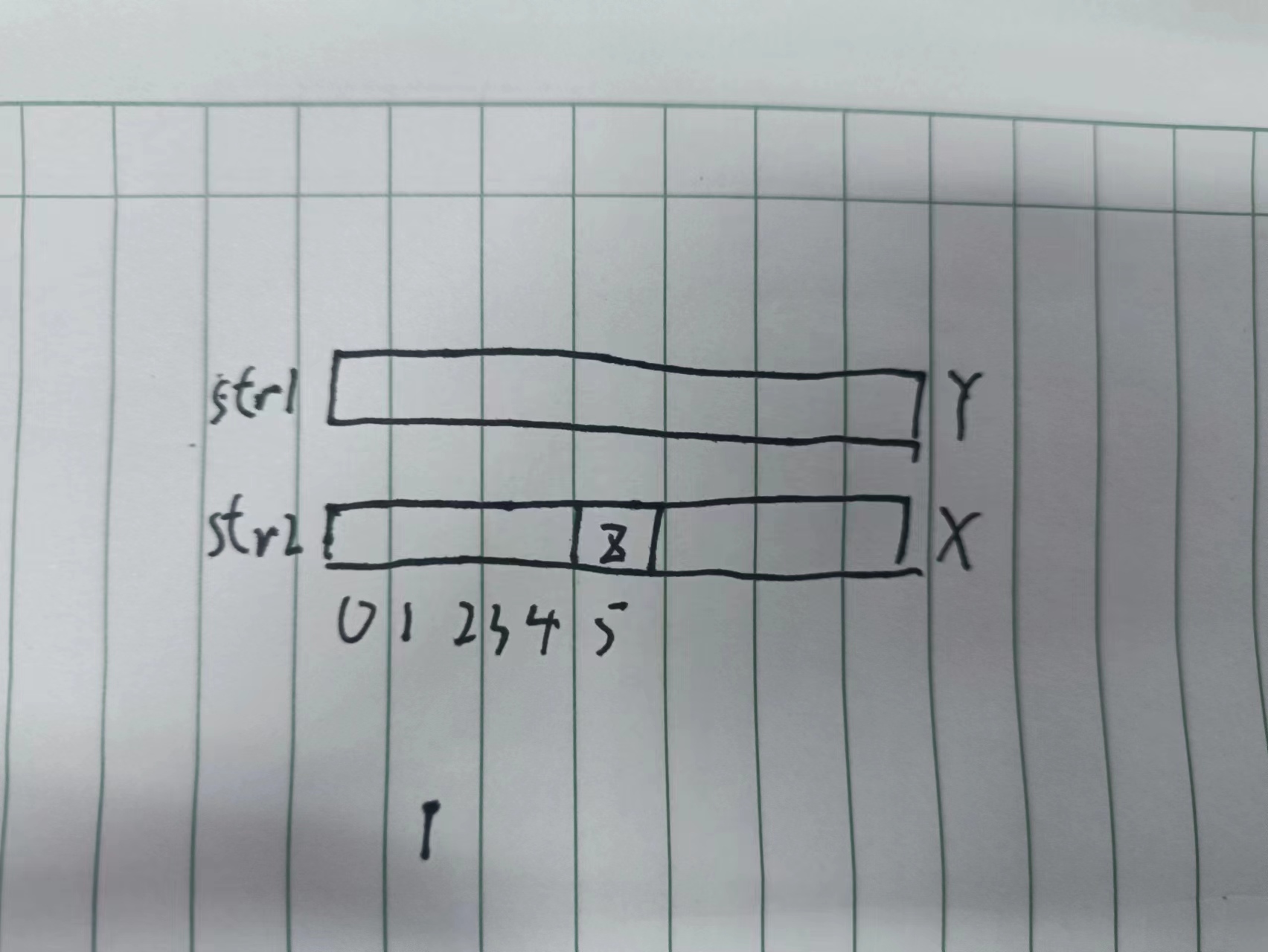
 就是从这个X Y为不同的地方 然后str2 Z和str1 Y继续匹配  如果再不相同呢 就找到Z 的next答案 然后从答案位置匹配... 如果一直next到0了 都没匹配成功 那就让str1的指针++ 也就是说从Y+1为开头继续匹配

解释一下原因

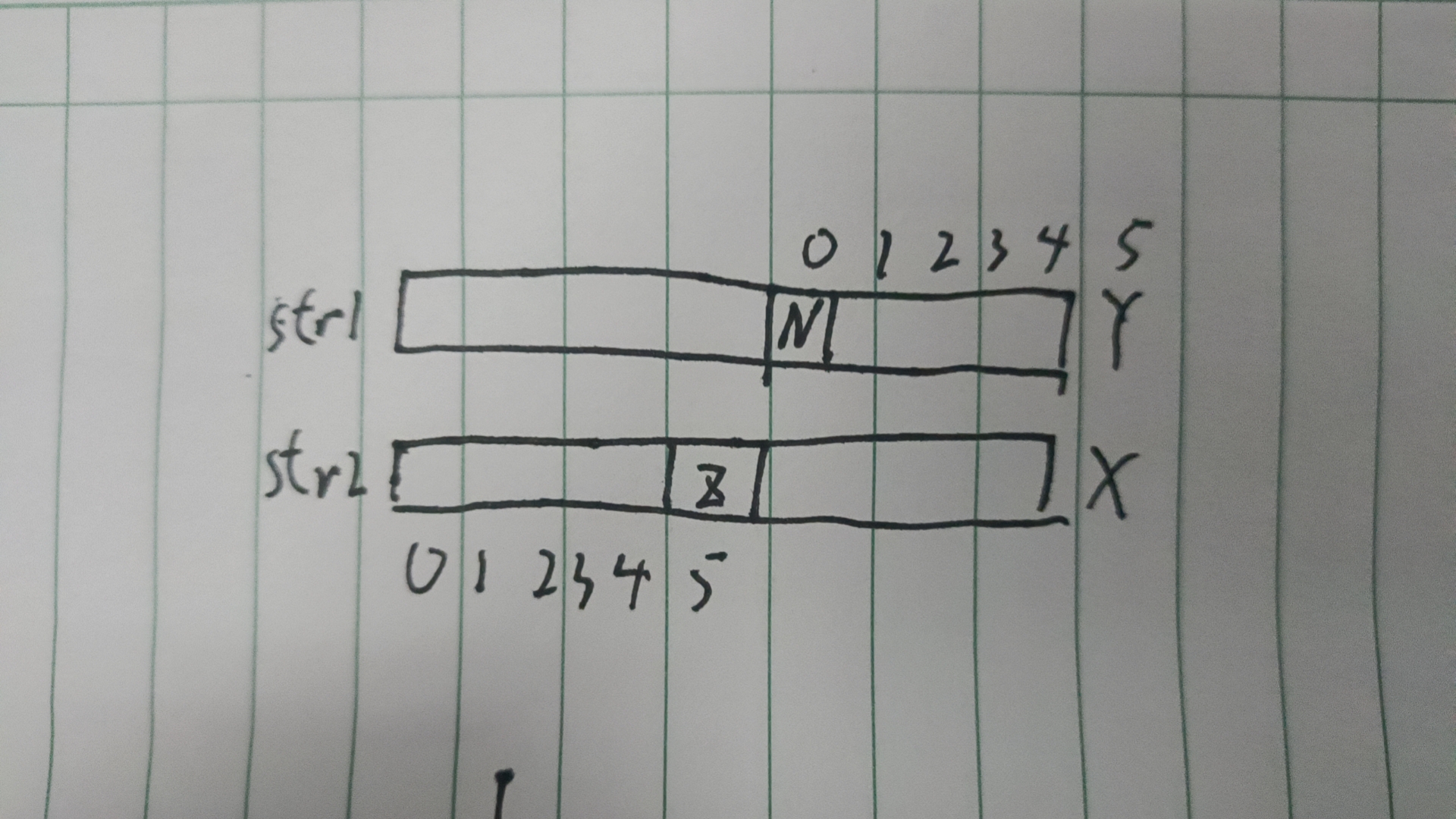
 首先我们知道Z和Y匹配 本质上是看以N开头的字符串和整个str2匹配 但是为什么N到Y之间的那段不用看了呢 首先对于str2来说 因为X位置的答案为5 那么str2的前五个(0-4)和后五个一定相等对吧  然后因为我们str1和str2 X Y之前的部分已经判断完相等了对吧  所以str2的0-4 等于 (x-5)~(x-1) 然鸡皮N~Y-1 又和 (x-5)~(x-1)一一对应 所以0-4和N~Y-1 就一定相等

那为什么不能是本质上N+1和0位置上匹配呢 额 因为X Y位置不同了 所以他到这一定会断掉

哎 是不是感觉还有哪不对 是的 这只能解释 N到Y-1的部分不用判断 但是解释不了为什么N之前的不用判断  

好 我们假设N之前有匹配的字符串 

对吧 假设S位置就可以匹配上了 那str2的前八个字符肯定和这个S开始的八个字符相同 再因为Y前的字符和X前的字符一 一相等 所以 S到Y-1 一定和下面str2中X-8到X-1的字符一 一对应 那也可以推出对于str2来说0~7和X-8到X-1相同 那X位置的next值应该是8啊 怎么能是5呢 这就冲突了 对不对 

所以基于这两个原理 str2可以直接和N进行比较

然后看做一个递归过程 如果我Z和Y没匹配上 那是不是又是一个同样的问题 哎 再去找Z的答案 一直找 找到str2开头0位置了 还没找到 那就说明真配不上 这整个一块都不行 你就把Y往下走吧

快速求next数组

反正跳出的时候 cn一定是当前位置的值 那到下一个循环的时候 cn就一定是上一个位置的结果 那str[cn]对应的是什么呢 就是要判断的位置啊 
因为next的值是前缀后缀相同的长度  如果这个位置的值是2  好 那我们就要判断第三个元素相不相同 如果相同 那就是值就是2+1 其实本来应该是前缀长度+1的位置的 但是正好 数组是从0开始的 都省了

那如果这个位置不同呢?  那就说明衔接不上 那我们再往前推一段

假如说a b a s a b a t g  这个数组 它对应位置的值为(是相等 不是对称)

         -1 0 0 1 0 1 2 3 

我们求g g位置本质是求t结尾的前缀后缀相同最大长度 a结尾的最大相同长度为3 哎 如果我这个t正好和第四个位置相同 是不是就直接套上了 可惜不同 那没办法 但是呢 也不一定直接为0 还要看我们3位置的值 因为你不能接在这个后面的话 那更短的位置呢 

假如这种情况 abagababs 我们求s位置的值 也就是以前一个字符结尾的那个值 虽然部门不能接到aba后面让最大相等长度为4 但是我们可以去看更前面 它和ab还是组成了前缀 后缀相同的

画个图直观理解一下

 

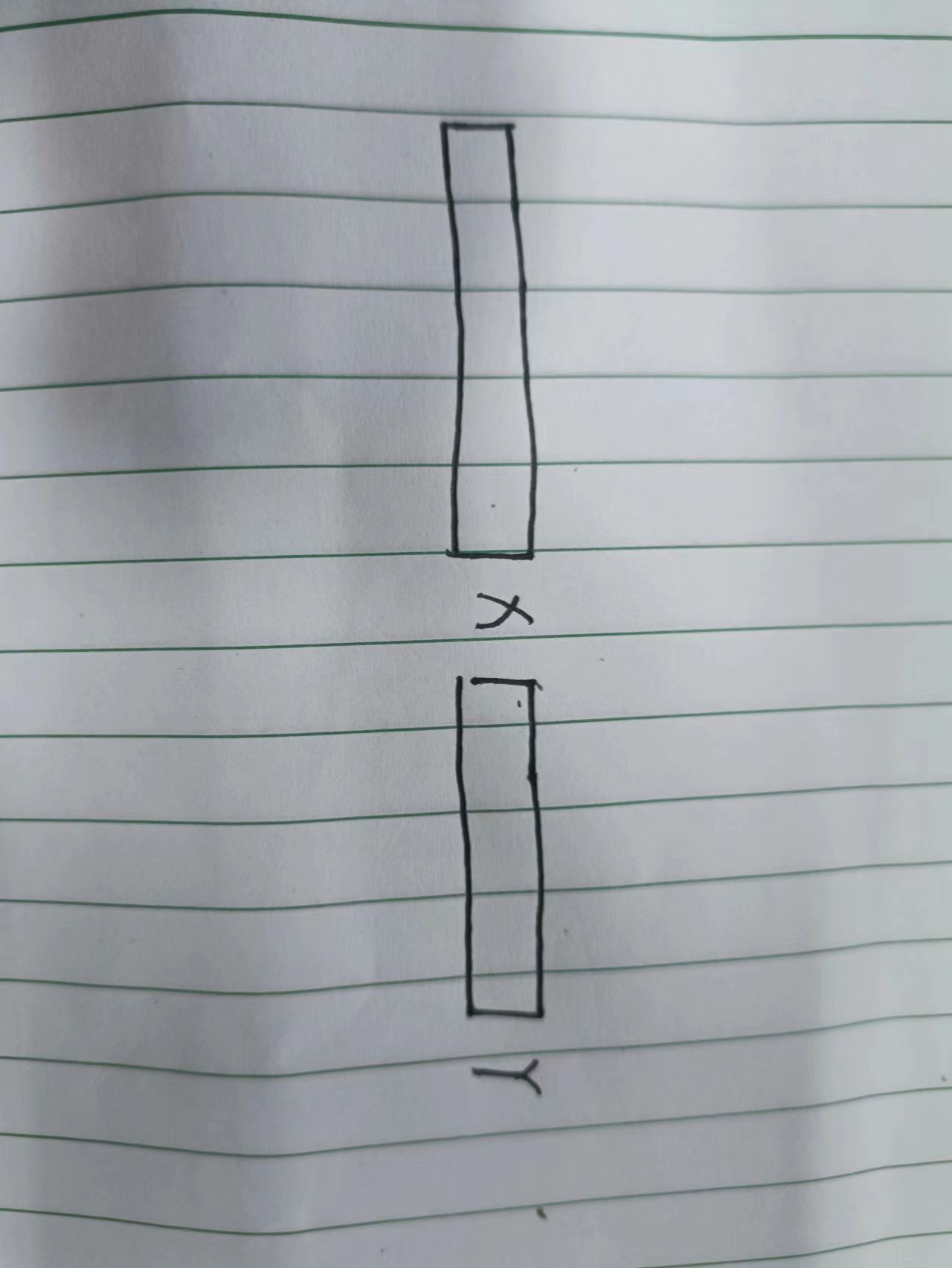
Y位置的结果 就是以Y-1结尾的最长相等前缀后缀 假如说已经求出来了 这两个方块区间代表 前缀和后缀 我们求Y+1的结果 那就是以Y结尾的最长相等前缀后缀  这两块区间肯定相等的 如果Y和X相等 那是最好的 我们直接上一个位置的值+1 就出结果了 但是不同呢?难道直接归零去比对吗 不 还可以优化

假如说x位置有值 这个值 就代表着前缀a 前缀b是相等的  那么在x的另一侧就有对应的 c 和d 相等

因为根据Y知道 x的左右两个大区间肯定是相等的

所以可以推出a和c相等 b和d相等

有了这几个条件 我们就知道了 a和d相等  所以Y如果和a的下一个字符配上了 那它的结果就等于x结果加1

那一直干到最开始都没匹配上 那就说明 没有了呗

OK我们开始coding

 public static int KMP(String str,String match) {
		char [] str1 = str.toCharArray();
		char [] str2 = match.toCharArray();
		int x = 0;
		int y = 0;
		int [] next = getnext(str2);
		while(x<str1.length&&y<str2.length) {
			if(str1[x]==str2[y]) {
				x++;
				y++;
			}else if(next[y]==-1){
				x++
			}else {
				y = next[y];
			}
		}
		return y == str2.length ? x - y : -1;//y走到头了 说明匹配出来了(y要比实际位置+1 走出while循环都这样) x走到头了说明没有
	}
    public static int [] getnext(char [] str) {
		int [] next = new int [str.length];
		next[0] = -1;
		next[1] = 0;
		int index = 2;
		int cn = 0;
		while(index<str.length) {
			if(str[index-1]==str[cn]) {
				next[index++] = ++cn;
			}else if(cn>0) {
				cn = next[cn];
			}else {
				next[index++] = 0;
			}
		}
		return next;
	}