今天的主角是：融合正余弦和折射反向学习的北方苍鹰优化算法(SCNGO)，算法由作者自行改进，目前应该没有文献这样做。

改进策略参照的上一期改进的麻雀优化算法，改进点如下：

①采用折射反向学习策略初始化北方苍鹰算法个体，基本思想是通过计算当前解的反向解来扩大搜索范围，借此找出给定问题更好的备选解；

②采用正余弦策略替换原始苍鹰算法的勘察阶段的位置更新公式；

③对正余弦策略的步长搜索因子进行改进；原始步长搜索因子呈线性递减趋势，不利于进一步平衡北方苍鹰算法的全局搜索和局部开发能力。

在CEC2005函数集上进行测试，结果如下：其中SCNGO为本文所提改进算法，DBO是蜣螂优化，GEO是金鹰优化，RIME是霜冰优化算法，BWO是白鲸优化算法，NGO是北方苍鹰优化。

算法迭代1000次，每种算法的粒子数设置为100。

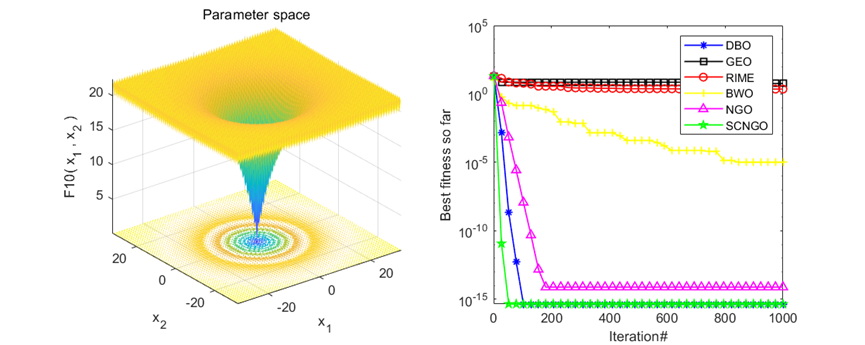
结果分析：在单峰值函数与多峰值函数的测试中可以看到，改进的北方苍鹰优化算法表现还是不错滴。

未改进的北方苍鹰(NGO)源代码展示：

%% 
function [Score,Best_pos,NGO_curve]=NGO(Search_Agents,Max_iterations,Lowerbound,Upperbound,dimensions,objective)
Lowerbound=ones(1,dimensions).*(Lowerbound);                              % Lower limit for variables
Upperbound=ones(1,dimensions).*(Upperbound);                              % Upper limit for variables
X=[];
X_new=[];
fit=[];
fit_new=[];
NGO_curve=zeros(1,Max_iterations);
for i=1:dimensions
    X(:,i) = Lowerbound(i)+rand(Search_Agents,1).*(Upperbound(i) -Lowerbound(i));              % Initial population
end
for i =1:Search_Agents
    L=X(i,:);
    fit(i)=objective(L);                    % Fitness evaluation (Explained at the top of the page. )
end
for t=1:Max_iterations  % algorithm iteration   
    %%  update: BEST proposed solution
    [best , blocation]=min(fit);
    if t==1
        xbest=X(blocation,:);                                           % Optimal location
        fbest=best;                                           % The optimization objective function
    elseif best<fbest
        fbest=best;
        xbest=X(blocation,:);
    end
    %% UPDATE Northern goshawks based on PHASE1 and PHASE2
    for i=1:Search_Agents
        %% Phase 1: Exploration
        I=round(1+rand);
        k=randperm(Search_Agents,1);
        P=X(k,:); % Eq. (3)
        F_P=fit(k);
        if fit(i)> F_P
            X_new(i,:)=X(i,:)+rand(1,dimensions) .* (P-I.*X(i,:)); % Eq. (4)
        else
            X_new(i,:)=X(i,:)+rand(1,dimensions) .* (X(i,:)-P); % Eq. (4)
        end
        X_new(i,:) = max(X_new(i,:),Lowerbound);X_new(i,:) = min(X_new(i,:),Upperbound);
        % update position based on Eq (5)
        L=X_new(i,:);
        fit_new(i)=objective(L);
        if(fit_new(i)<fit(i))
            X(i,:) = X_new(i,:);
            fit(i) = fit_new(i);
        end
        %% END PHASE 1
        %% PHASE 2 Exploitation
        R=0.02*(1-t/Max_iterations);% Eq.(6)
        X_new(i,:)= X(i,:)+ (-R+2*R*rand(1,dimensions)).*X(i,:);% Eq.(7)
        
        X_new(i,:) = max(X_new(i,:),Lowerbound);X_new(i,:) = min(X_new(i,:),Upperbound);
        
        % update position based on Eq (8)
        L=X_new(i,:);
        fit_new(i)=objective(L);
        if(fit_new(i)<fit(i))
            X(i,:) = X_new(i,:);
            fit(i) = fit_new(i);
        end
        %% END PHASE 2
    end% end for i=1:N
    %%
    %% SAVE BEST SCORE
    best_so_far(t)=fbest; % save best solution so far
    average(t) = mean (fit);
    Score=fbest;
    Best_pos=xbest;
    NGO_curve(t)=Score;
end
en

改进的北方苍鹰部分代码展示

clear all 
clc
close all


PD_no=100;      %Number of sand cat
F_name='F10';     %Name of the test function
Max_iter=1000;    %Maximum number of iterations
[LB,UB,Dim,F_obj]=CEC2005(F_name); %Get details of the benchmark functions




%% BWO    
[Best_pos,Best_score, BWO_cg_curve ] = BWO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call BWO
fprintf ('Best solution obtained by BWO: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by BWO  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);


%% DBO    
[Best_pos,Best_score, DBO_cg_curve ] = DBO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call DBO
fprintf ('Best solution obtained by DBO: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by DBO  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);


%% GEO
options.PopulationSize = PD_no;
options.MaxIterations  = Max_iter;
[Best_pos,Best_score, GEO_cg_curve ] =  GEO (F_obj,Dim,LB,UB,options);  % Call GEO
fprintf ('Best solution obtained by GEO: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by GEO  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);


%% RIME    
[Best_pos,Best_score, RIME_cg_curve ] = RIME(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call RIME
fprintf ('Best solution obtained by RIME: %s\n', num2str(Best_score,'%e  '));
display(['The best optimal value of the objective funciton found by RIME  for ' [num2str(F_name)],'  is : ', num2str(Best_pos)]);


%% NGO
[Best_PD,PDBest_P,NGO_cg_curve]=NGO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call NGO
fprintf ('Best solution obtained by NGO: %s\n', num2str(Best_PD,'%e  '));
display(['The best optimal value of the objective funciton found by NGO  for ' [num2str(F_name)],'  is : ', num2str(PDBest_P)]);


%% SCNGO
[BsSCNGO,BpSCNGO,SCNGO_cg_curve]=SCNGO(PD_no,Max_iter,LB,UB,Dim,F_obj); % Call MSCNGO
fprintf ('Best solution obtained by SCNGO: %s\n', num2str(BsSCNGO,'%e  '));
display(['The best optimal value of the objective funciton found by SCNGO  for ' [num2str(F_name)],'  is : ', num2str(BpSCNGO)]);




CNT=40;
k=round(linspace(1,Max_iter,CNT)); %随机选CNT个点
% 注意：如果收敛曲线画出来的点很少，随机点很稀疏，说明点取少了，这时应增加取点的数量，100、200、300等，逐渐增加
% 相反，如果收敛曲线上的随机点非常密集，说明点取多了，此时要减少取点数量
iter=1:1:Max_iter;
figure('Position',[154   145   894   357]);
subplot(1,2,1);
func_plot(F_name);     % Function plot
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([F_name,'( x_1 , x_2 )'])
subplot(1,2,2);       % Convergence plot
h2 = semilogy(iter(k),DBO_cg_curve(k),'b-*','linewidth',1);
hold on
h3 = semilogy(iter(k),GEO_cg_curve(k),'k-s','linewidth',1);
hold on
h4 = semilogy(iter(k),RIME_cg_curve(k),'r-o','linewidth',1);
hold on
h5 = semilogy(iter(k),BWO_cg_curve(k),'y-+','linewidth',1);
hold on
h6 = semilogy(iter(k),NGO_cg_curve(k),'m-^','linewidth',1);
hold on
h1 = semilogy(iter(k),SCNGO_cg_curve(k),'g-p','linewidth',1);
xlabel('Iteration#');
ylabel('Best fitness so far');
legend('DBO','GEO','RIME','BWO','NGO','SCNGO');

完整代码获取方式，后台回复关键词：

SCNGO