小蓝本 第一本《因式分解技巧》第四章 拆项与添项 笔记(第四天)
- 前言
- 拆项与添项
- 目的
- 方法
- 分组分解走平均分配
- 分组分解走瞄准公式
- 旧事重提第二章公式(9)
- 好题
- 习题4
- 题目
- 题解
- 错题
- 题号
- 改错
- 经验
前言
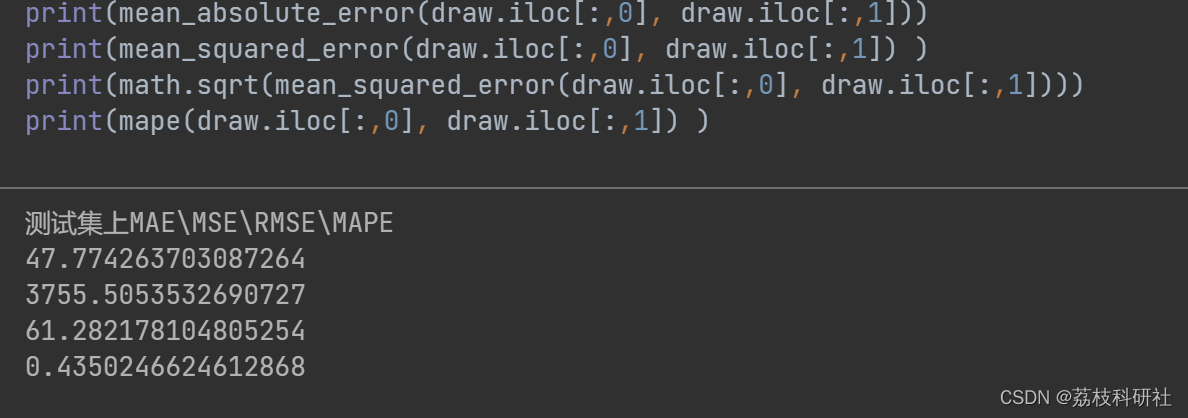
芜湖,坚持做小蓝本的第四天,今天的知识点相对轻松,当然是基于昨天的基础之上的一个优化。昨天的博客
拆项与添项
目的
拆项或添项完,在适当分组后使得每一组都可以“提”或“代”,同时组与组之间也可以“提”或“代”。
方法
以分组分解的两种走向作为拆项与添项的分类。
分组分解走平均分配
场景: 整式只有奇数项
方法:将一项拆成两项
ps : 如果一个整式是按某个字母的升幂或降幂排列的,拆开中项为宜。
分组分解走瞄准公式
场景 : 配成乘法公式缺一个成分
方法 : 拆项或添项满足乘法公式(多练习,一眼看出)
ps : 无中生有
旧事重提第二章公式(9)
之前我们在第二章里,通过 a 6 − b 6 a^6-b^6 a6−b6 两种方式的对比推出了 公式(9) a 4 + a 2 b 2 + b 4 = ( a 2 + a b + b 2 ) ( a 2 − a b + b 2 ) a^4+a^2b^2+b^4=(a^2+ab+b^2)(a^2-ab+b^2) a4+a2b2+b4=(a2+ab+b2)(a2−ab+b2) 。同时我也透漏了,第四章有新的解法,让我们来看一下:
a4+a2b2+b4
= ( a4+2a2b2+b4 ) - a2b2
= ( a2+b2)2 - ( ab )2
= (a2 +ab+b2)(a2-ab+b2)
好题
积累的一道好题,找别人去炫耀一下
− a 4 − b 4 − c 4 + 2 a 2 b 2 + 2 b 2 c 2 + 2 c 2 a 2 -a^4-b^4-c^4+2a^2b^2+2b^2c^2+2c^2a^2 −a4−b4−c4+2a2b2+2b2c2+2c2a2
- = − ( a 4 + b 4 + c 4 − 2 a 2 b 2 − 2 b 2 c 2 − 2 c 2 a 2 ) -(a^4+b^4+c^4-2a^2b^2-2b^2c^2-2c^2a^2) −(a4+b4+c4−2a2b2−2b2c2−2c2a2)
- = − ( a 4 + b 4 + c 4 + 2 a 2 b 2 − 2 b 2 c 2 − 2 c 2 a 2 − 4 a 2 b 2 ) -(a^4+b^4+c^4+2a^2b^2-2b^2c^2-2c^2a^2-4a^2b^2) −(a4+b4+c4+2a2b2−2b2c2−2c2a2−4a2b2)
- = − [ ( a 2 + b 2 − c 2 ) 2 − ( 2 a b ) 2 ] -[(a^2+b^2-c^2)^2-(2ab)^2] −[(a2+b2−c2)2−(2ab)2]
- = − ( a 2 + b 2 − c 2 + 2 a b ) ( a 2 + b 2 − c 2 − 2 a b ) -(a^2+b^2-c^2+2ab)(a^2+b^2-c^2-2ab) −(a2+b2−c2+2ab)(a2+b2−c2−2ab)
- = − [ ( a + b ) 2 − c 2 ] [ ( a − b ) 2 − c 2 ] -[(a+b)^2-c^2][(a-b)^2-c^2] −[(a+b)2−c2][(a−b)2−c2]
- = − ( a + b + c ) ( a + b − c ) ( a − b + c ) ( a − b − c ) -(a+b+c)(a+b-c)(a-b+c)(a-b-c) −(a+b+c)(a+b−c)(a−b+c)(a−b−c)
- = ( a + b + c ) ( a + b − c ) ( a − b + c ) ( b + c − a ) (a+b+c)(a+b-c)(a-b+c)(b+c-a) (a+b+c)(a+b−c)(a−b+c)(b+c−a)
① 提公因式
② 拆项
③ 公式(8)
④ 公式(1)
⑤ 公式(4)(5)
⑥ 公式(1)
⑦ 去符号
注:根据几何可知,一个三角形三条边的长分别为a、b、c,那么三角形的面积
▲
=
√
s
(
s
−
a
)
(
s
−
b
)
(
s
−
c
)
▲=√s(s-a)(s-b)(s-c)
▲=√s(s−a)(s−b)(s−c)
其中
s
=
(
a
+
b
+
c
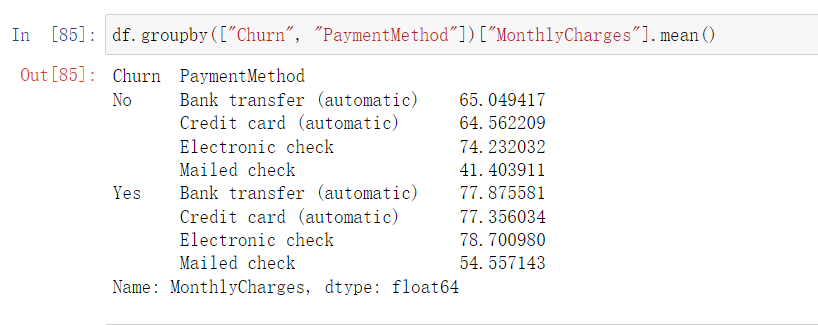
)
/
2
s=(a+b+c)/2
s=(a+b+c)/2 三角形周长的一半。
这个整式实际上是 16 ▲ 2 16▲^2 16▲2
习题4
题目

题解

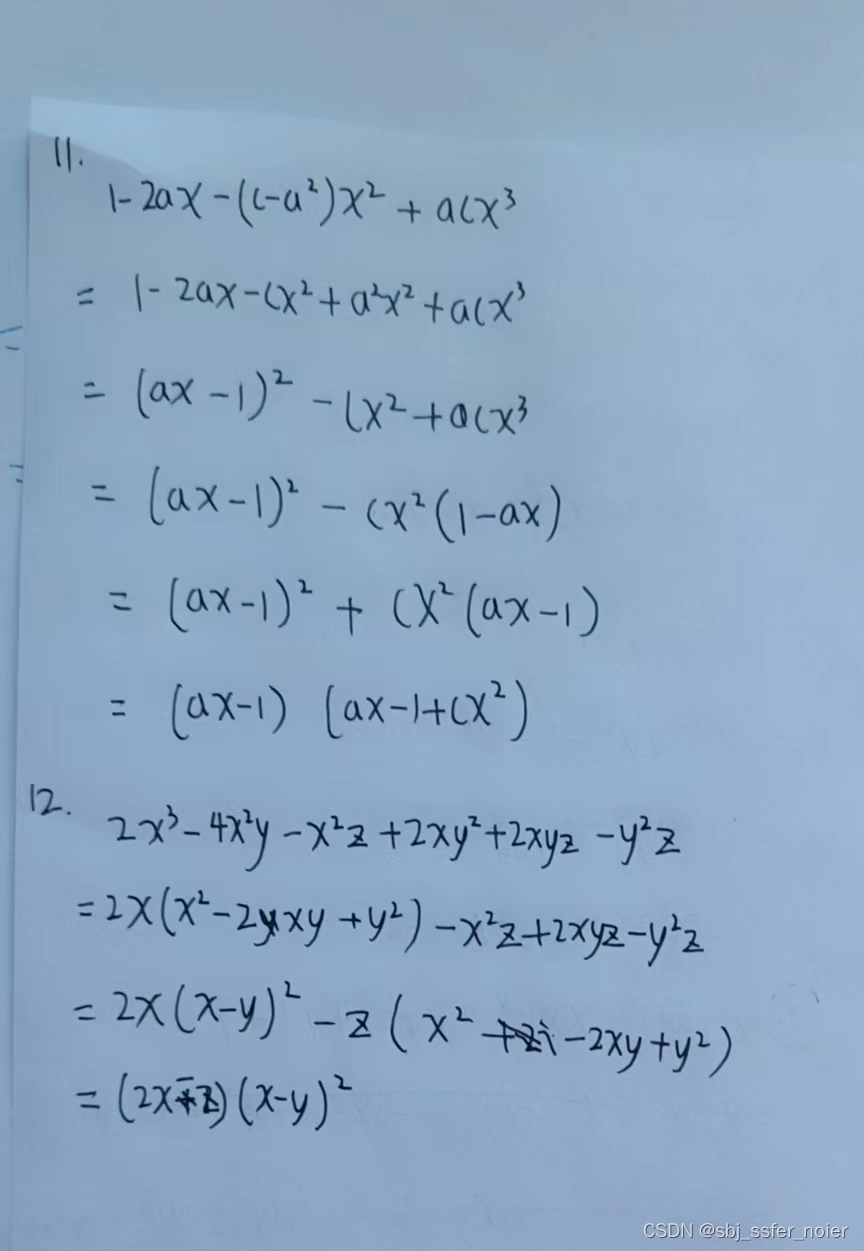
错题
题号
8
改错
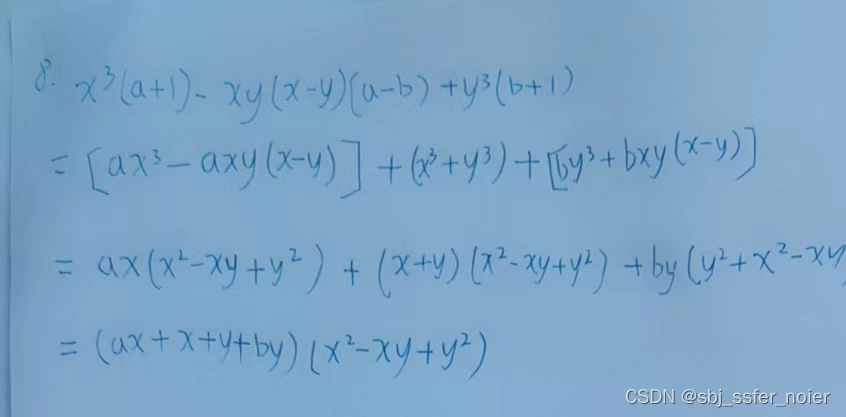
经验
加强分组的练习