字符串
给定一个数值的数组,要求组合最小的数值。
public String PrintMinNumber(Integer [] s) {
if(s==null) return null;
String s1="";
ArrayList<Integer> list=new ArrayList<Integer>(Arrays.asList(s));
// for(int i=0;i<s.length;i++){
// list.add(s[i]);
// }
Collections.sort(list,new Comparator<Integer>(){
//数组里的数两两组合比较,按照比较值更得的顺序升序排序
public int compare(Integer str1,Integer str2){
String s1=str1+""+str2;
String s2=str2+""+str1;
return s1.compareTo(s2);
//变成-s1.compareTo(s2)就是降序排序了
}
});
for(int j:list){
s1+=j;
}
return s1;
}
*最长回文串
马拉车算法模板
import java.util.*;
public class Main {
public static void main(String a[]) {
Scanner in = new Scanner(System.in);
String str = in.next();
char s[] = str.toCharArray();
s = preProcess(s);
int len = s.length;
int iMirror = 0, rMax = 0, iCenter = 0;
int dp[] = new int[len];
dp[0] = 0;
int max = 0;
for (int i = 1; i < len - 1; i++) {
//计算镜像下标
iMirror = 2 * iCenter - i;
if (i < rMax) {
dp[i] =Math.min(dp[iMirror],rMax-i+1);
} else {
dp[i] = 1;
}
//中心拓展
while(i+dp[i]<len&&i-dp[i]>=0&&s[i+dp[i]]==s[i-dp[i]]){
dp[i]++;
}
if(i+dp[i]-1>rMax) {
rMax = i+dp[i]-1;
iCenter = i;
if(max<dp[i]-1)max = dp[i]-1;
}
}
System.out.println(max);
}
public static char [] preProcess(char [] s) {
int len = (s.length << 1) + 1;
char a[] = new char[len];
for (int i = 0; i < len; i++) {
if (i & 1 == 0) a[i] = '#';
else a[i] = s[i >> 1];
}
return a;
}
}
树
二叉排序树形状数量
故对于一个节点数为n的二叉排序树,当根节点值为i时,左子树有i-1个节点,右子树有n-i-1个节点,求积。且左子树与右子树均为二叉排序树,所以当根节点值为i时,二叉排序树总共有种形状当然需要取模,那么对于一个节点数为n的二叉排序树其形状数量为
当二叉树节点数为0时,默认为1,便于计算,所以可以依据上述公式,递归计算给定数量的二叉排序树的形状数。
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* 计算二叉树个数
* @param n int整型 二叉树结点个数
* @return int整型
*/
private static int mod = 1000000007;
public int numberOfTree (int n) {
// 直接返回
if (n == 1 || n == 2){
return n;
}
long[] dp = new long[n+1];
dp[0] = 1;
dp[1] = 1;
dp[2] = 2;
for (int i = 3;i < dp.length;++i){
long count = 0;
for (int j = 1;j <= i;++j){
count += ((dp[i-j]*dp[j-1])%mod);
}
dp[i] = (int) (count % mod);
}
return (int) dp[n];
}
}
表达式计算
思路
排列组合
无重复字母(不可复选)
递归回溯
有重复字母(不可复选)
递归回溯+剪枝(排序,保证每次放入字符visit[i]时候,如果前一个字符和i相同且那么visit[i-1]为true可以放入,否则不能放入。)
如: a1a2bcc,第一次a1a2b…,第二次a2时候就剪枝。
有重复字符串的排列组合

- 回溯+剪枝
字符串长度1~9,可以使用递归,同时set去重 - set去重效率较低,另外一种(剪枝)思路:对字符排序,每次判断当前元素能否加入的时候,要求 s[i]==s[i-1]的时候需要s[i-1] 已经添加入结果中。或者当前遍历的元素下标等于0.
if(i>0 || s[i]==s[i-1]&&!select[i-1]) continue;
class Solution {
public String[] permutation(String S) {
char a[] = S.toCharArray();
HashSet<String> set = new HashSet<>();
boolean select[] = new boolean[a.length];
trace(set,a,select,0,new LinkedList<Character>());
Iterator<String> ite = set.iterator();
String res [] = new String[set.size()];
for(int i=0;i<set.size();i++){
res[i] = ite.next();
}
return res;
}
public void trace(Set<String> set,char [] a, boolean [] select,int index,LinkedList<Character> res ) {
if(index>=a.length) {
String s = "";
for(int i=0;i<res.size();i++){
s+=res.get(i);
}
set.add(s);
}
for(int j=0;j<a.length;j++){
if(!select[j]){
select[j]=true;
res.add(a[j]);
trace(set,a,select,index+1,res);
res.removeLast();
select[j]=false;
}
}
}
}
下一个排列

class Solution {
public void nextPermutation(int[] nums) {
boolean find = false;
//交换 找更大的下一个数 如果数组从右向左已经是递增的那么 肯定不是在递增的中进行交换,这样只会更小
//除非已经是最大数,那就整个数组翻转。
//若是找到如 (2 5) 4 3 1 这种,5比2大,那么就从2下手,5左边是递减的序列,根据2在5~1的序列中找第一个比2大的数,交换
// 此时能 3 5 4 2 1 保证5左边是递减序列,3也是刚好比2大的数,翻转5~1 31245 就是要求序列。
for(int i=nums.length-1;i>=1;i--){
if(nums[i]>nums[i-1]){
find = true;
//从右往左 找到第一个比当前数大的
int right = nums.length-1;
while(right > i-1 && nums[right] <= nums[i-1]) right--;
swap(nums,i-1,right);
reverse(nums,i,nums.length-1);
break;
}
}
if(!find){
reverse(nums,0,nums.length-1);
}
}
public void swap(int a[],int i,int j){
int t=a[i];
a[i]=a[j];
a[j]=t;
}
public void reverse(int a[],int i,int j){
while(i<j){
swap(a,i,j);
i++;
j--;
}
}
}
素数
*素数伴侣
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DmLdyHOW-1690390210180)(https://s2.loli.net/2022/07/16/zH7D3cBsYoQgG1a.jpg)]
import java.util.*;
public class Main {
//
public static void main(String s[]) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
ArrayList<Integer> evens = new ArrayList<>();
ArrayList<Integer> odds = new ArrayList<>();
for (int i = 0; i < n; i++) {
int t = in.nextInt();
if ((t & 1) == 0) evens.add(t);
else odds.add(t);
}
if (odds.size() == 0 || evens.size() == 0) {
System.out.println(0);
return ;
}
int matchEven [] = new int [evens.size()];
int count = 0;
for (int i = 0; i < odds.size(); i++) {
//用于标记偶数是否已经匹配过
boolean [] select = new boolean [evens.size()];
//查找第i个奇数是否能匹配到对应的伴侣 能+1。
if (find(odds.get(i), matchEven, evens, select)) {
count ++;
}
}
System.out.println(count);
}
static boolean find(int x, int matchEven[], List<Integer> evens,
boolean select[]) {
for (int i = 0; i < evens.size(); i++) {
//如果i位置偶数没有访问过
if (!select[i] && isPrime(evens.get(i) + x)) {
//如果x能和第i个偶数 作为伴侣
select[i] = true;
//如果i位置偶数还没有伴侣,那就与x组成伴侣
//如果已经有伴侣matchEven[i],并且这个伴侣还能找到新的伴侣.
// 那就把原来matchEven[] -->i 让给x,
if (matchEven[i] == 0 || find(matchEven[i], matchEven, evens, select)) {
matchEven[i] = x;
return true;
}
}
}
//找不到
return false;
}
static boolean isPrime(int a) {
int p = (int) Math.sqrt(a);
for (int i = 2; i <= p; i++) {
if (a % i == 0) return false;
}
return true;
}
}
区间素数 计数
-
区间范围小的话,直接枚举
-
范围大的话,常用打表法
- 埃式筛选法
如果x是素数的话,2x、3x、4x一定不是素数,一个合数一定是某一个素数的倍数。
详细
class Solution {
public int countPrimes(int n) {
int[] isPrime = new int[n];
//1 表示素数
Arrays.fill(isPrime, 1);
int ans = 0;
for (int i = 2; i < n; ++i) {
// 比如2*2求得合数4,两个最小的素数求得最小合数4,那么2~4之间3一定合数不可达,那么一定是素数。同理5. 3~4~6。每一轮筛选过后一定能得到至少一个素数。
if (isPrime[i] == 1) {
ans += 1;
if ((long) i * i < n) {
for (int j = i * i; j < n; j += i) {
isPrime[j] = 0;
}
}
}
}
return ans;
}
}
- 线性筛选法
相比于埃式筛选区别,埃氏筛其实还是存在冗余的标记操作,比如对于45这哥合数,同时会被3和5标记为合数,造成冗余计算,而线性筛选,
搜索
994. 腐烂的橘子
广搜
class Solution {
class Node{
public int x;
public int y;
Node(int x,int y){
this.x = x;
this.y = y;
}
}
public int orangesRotting(int[][] grid) {
//广搜
LinkedList<Node> temp=null;
LinkedList<Node> list = new LinkedList<>();
LinkedList<Node> list2 = new LinkedList<>();
int n = grid.length;
int m = grid[0].length;
System.out.println(n+" "+m);
//初始化
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(grid[i][j]==2){
list.add(new Node(i,j));
}
}
}
//没有腐烂的橘子 但是有 未腐烂的橘子 返回-1 否则返回0
if(list.isEmpty()){
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(grid[i][j]==1) return -1;
}
}
return 0;
}
//遍历
int times = 0;
while(!list.isEmpty()){
while(!list.isEmpty()){
Node node = list.removeLast();
System.out.print(" "+node.x+" "+node.y);
vis(node,grid,list2);
}
System.out.println();
times++;
//交换
temp = list2;
list2 = list;
list = temp;
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
if(grid[i][j]==1) return -1;
}
}
return times-1;
}
void vis(Node node,int [][]grid,LinkedList<Node> list){
int x = node.x,y = node.y;
//左
if(x>0&&grid[x-1][y]==1){
list.add(new Node(x-1,y));
grid[x-1][y]=2;
}
if(y>0&&grid[x][y-1]==1){
list.add(new Node(x,y-1));
grid[x][y-1]=2;
}
if(x<grid.length-1&&grid[x+1][y]==1){
list.add(new Node(x+1,y));
grid[x+1][y] = 2;
}
if(y<grid[0].length-1&&grid[x][y+1]==1){
list.add(new Node(x,y+1));
grid[x][y+1] = 2;
}
}
}
动态规划
lintcode
上升子序列
求数组中最长的上升子序列、连续子序列。
连续 f[j] = f[j-1]+1 ,a[j-1]<a[j]
非连续 f[j] = f[j-1]+1 , a[j] >(a[0~j-1])
- 非连续优化 贪心+二分查找 (类似插入排序)
对于一个上升子序列,显然其结尾元素越小,越有利于在后面接其他的元素,也就越可能变得更长。
dp[i]原有代表前i个字符串最长的上升自序列,转换为 长度为i的上升子序列时尾部的最小元素。
思路:
- 遍历一个个元素的过程中维护B[]数组(下标0~i代表上升子序列的长度,B[i]存的是最长连续子序列长度i时最小的元素值,往后遍历只有更新最右边元素的元素值,才有可能往后遍历的过程中拼接上更长的序列,贪心)。
- 如果A[i]大于B队列尾部元素,B一定是一个连续的上升序列,所以直接二分查找B中第一个大于A[i]元素的位置,然后替换该元素。最后返回B的长度即可。
二维上升子序列问题 - 俄罗斯套娃
n个(w,h)的信封要求最多能套多少层信封。思路:相当于二维的最长上升子序列问题,信封是没有循序要求的,可以将信封按宽或者高度先排序,然后再一维上遍历h的最长上升子序列,要求 信封i的w不等于信封i-1的w的上生子序列。也可以在排序的时候按w相等h逆序排序,这样就不存在w相同,h递增的情况被选上。
最长公共子序列问题
-
连续 f[i][j] = f[i-1][j-1]+1 当且仅当 a[i]==B[j],否则为0。
-
非连续
最后一位相等,f[i][j] = Max(f[i-1][j-1]+1,f[i][j])
O(N2)
打劫房屋
- 非环形
f[i] = Max(f[i-1],f[i-2]+A[i]) - 环形
- 第一个偷 f[i] = Max(f[i-1],f[i-2]+A[i]) [0,i-2]
- 第一个不偷 f[i] = Max(f[i-1],f[i-2]+A[i]) [1,i-1]
综合比较大小。
买卖股票
买卖股票,买卖一次,单调递减栈,找最大差值。
买卖两次呢,N次呢,无限次数呢?有无冷却期?
买卖股票,给定P天股价,选择买卖n次,约定可以或者不可以当天卖出当天买入。
思路:
一种解法团灭买卖股票问题
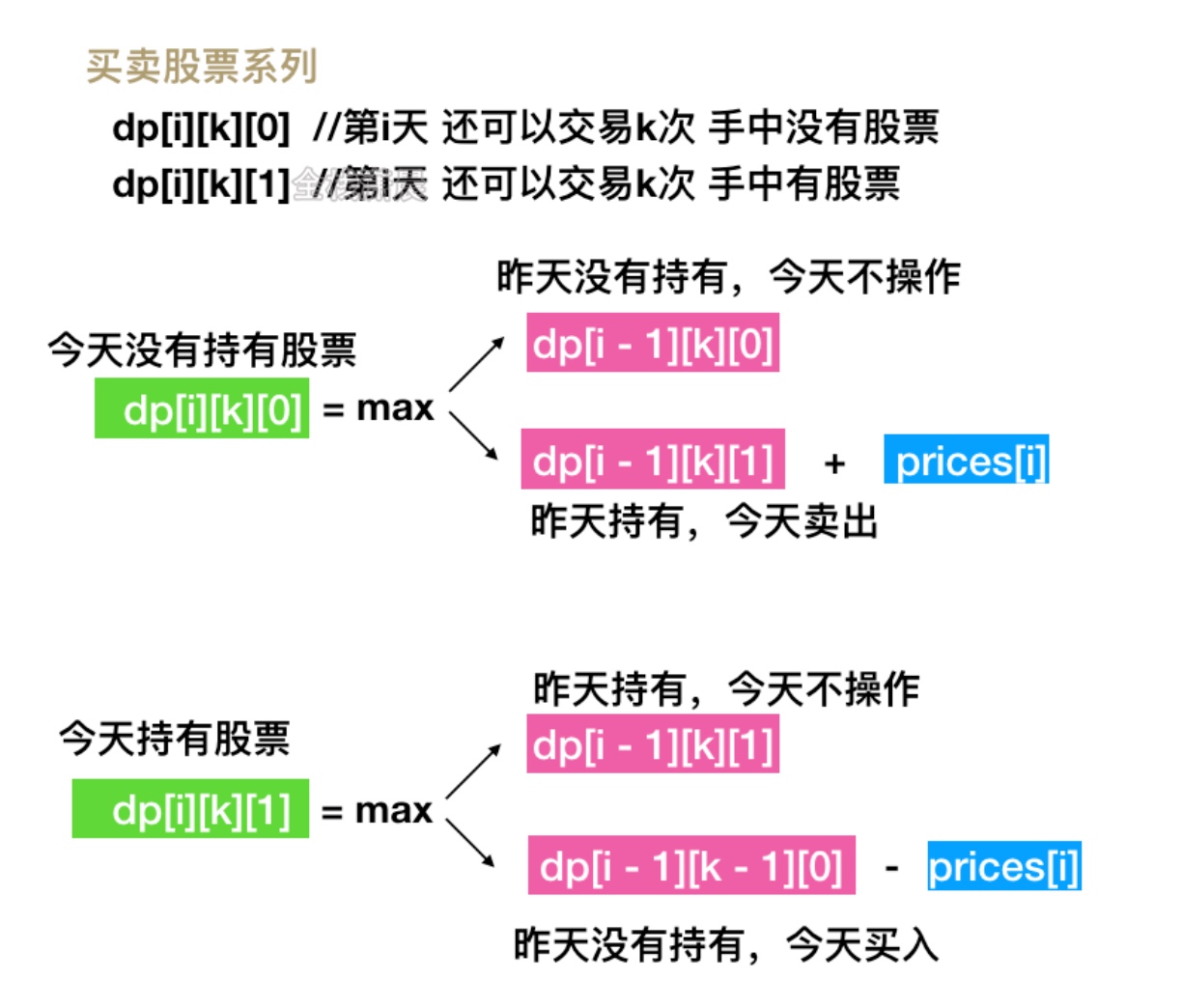
注意其中k是允许最大交易次数,今天买入(buy)的时候记一次交易。那么当前买入之前最大允许交易次数就是k-1次。
//几种初始状态
1. 假设第1天才开始交易,那么没交易之前状态
dp[0][..][0]=0 第0天未开盘,未持有也无花费
dp[0][..][1]= -MIN_VALUE 第0天还未开盘,持有是不可能的
2. 假设k=1是允许最大交易次数为1次,0不允许交易
dp[..][0][0]=0 不管哪一天,未持有股票也未交易收益都为0
dp[..][0][1]= -MIN_VALUE 不管哪一天,尚未交易却持有不可能情况
买卖k次
for(int i=1;i<=n;i++){
for(int j=max_k;j>=1;j--){
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-1天未持有 即买入, 记录买入消耗
dp[i][k][1] = max(dp[i-1][k][1],dp[i-1][k-1][0]-p[i]);
}
}
//此处k倒序遍历,正序遍历都可。
// 因为 dp[i][k][0] -- dp[i-1][k][1], dp[i][k][1] -- dp[i-1][k-1][0]
// (x,y)与(x-1,y) or(x-1,y+1) 数据有关
// (x,y)与(x-1,y) or (x-1,y-1) 有关。 j不论从左还是往右遍历都能基于之前数据计算
// 实际过程中,正序还是逆序遍历,看子问题是否已经计算。
for (int i = 0; i <= n; i++) {
for (int j = max_k; j >= 0; j--) {
if (i == 0) {
dp[0][j][0] = 0;
dp[0][j][1] = Integer.MIN_VALUE;
}
if (j == 0) {
dp[i][0][0] = 0;
dp[i][0][1] = Integer.MIN_VALUE;
} else {
if (i == 0) {
dp[0][j][0] = 0;
dp[0][j][1] = Integer.MIN_VALUE;
} else {
//当天卖出
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i-1]);
//当天买入
dp[i][j][1] = Math.max(dp[i - 1][j][1],
dp[i - 1][j - 1][0] - prices[i-1]);
}
}
}
}
// k 是不能优化掉,但是0,1持有未持有是可以优化掉的,可以定义两个数组 buy[i][j],sell[i][j] 分别表示前i天最多交易j次的持有和未持有的状态,不过效果不大。
买卖一次
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][1][0] = max(dp[i-1][1][0],dp[i-1][1][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-1天未持有 即买入, 记录买入消耗
dp[i][1][1] = max(dp[i-1][1][1],dp[i-1][0][0]-p[i]);
= max(dp[i-1][1][1], - p[i]); //因为前i-1天未持有也就未交易 收益为0;
//因为dp[i][1][0]只有交易一次,二维可以优化掉。
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
'//初始化边界值'
dp[0][0] = 0;
dp[0][1] = -p[0];
dp[i][0] = max(dp[i-1][0],dp[i-1][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-1天未持有 即买入, 记录买入消耗
dp[i][1] = max(dp[i-1][1], - p[i]);
//状态压缩
//因为dp[i] 只与dp[i-1]有关,只与上一次记录有关。
//注意dp[0]与dp[1]的计算循序。一次循环的计算结果 是基于上一次循环计算的结果,表示dp[i][0]与dp[i-1][0]之间的关系。
for(int i=0;i<p.length;i++){
dp[0] = max(dp[0],dp[1]+p[i])
dp[1] = max(dp[1],-p[i])
}
//语意化 第一天卖出
sell = 0
buy = -p[0]
sell = max(sell,buy+p[i]) //卖出收益
buy = max(buy,-p[i]) //买入消耗
买卖2次
'交易第2次'
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][2][0] = max(dp[i-1][2][0],dp[i-1][2][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-1天未持有 即买入, 记录买入消耗
dp[i][2][1] = max(dp[i-1][2][1],dp[i-1][1][0]-p[i]);
'交易第1次'
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][1][0] = max(dp[i-1][1][0],dp[i-1][1][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-1天未持有 即买入, 记录买入消耗
dp[i][1][1] = max(dp[i-1][1][1],dp[i-1][0][0]-p[i]);
= max(dp[i-1][1][1], - p[i]); //因为前i-1天未持有也就未交易 收益为0;
//k=2,直接枚举所有交易次数 循环的结果
dp[i][2][0] = Math.max(dp[i - 1][2][0], dp[i - 1][2][1] + prices[i])
dp[i][2][1] = Math.max(dp[i - 1][2][1], dp[i - 1][1][0] - prices[i])
dp[i][1][0] = Math.max(dp[i - 1][1][0], dp[i - 1][1][1] + prices[i])
dp[i][1][1] = Math.max(dp[i - 1][1][1], dp[i - 1][0][0] - prices[i])
= Math.max(dp[i - 1][1][1], -prices[i])// k=0时 没有交易次数,dp[i - 1][0][0] = 0
'直接状态压缩,i只与i-1行记录有关有关' 优化掉i
//通过计算顺序表示当前计算取自上一次循环计算结果关系。
// dp[2][0] 最多交易2次未持有股票最大收益
dp[2][0] = max(dp[2][0] ,dp[2][1]+p[i]);
dp[2][1] = max(dp[2][1],dp[1][0]-p[i]);
dp[1][0] = max(dp[1][0],dp[1][1]+p[i]);
dp[1][1] = max(dp[1][1],dp[0][0]-p[i]);
//语义化
//第一天不持有
sell2 = sell1 = 0
//第一天买入
buy2 = buy1 = -p[0]
sell2 = max(sell2 ,buy2+p[i]); //第二次卖出
buy2 = max(buy2,sell1-p[i]); //第二次买入
sell1 = max(sell1,buy1+p[i]);//第一次卖出
buy1 = max(buy1, 0 -p[i]);//第一次买入
买卖2次(k次同)
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 两次交易所能获得的最大收益
* @param prices int整型一维数组 股票每一天的价格
* @return int整型
*/
public int maxProfit (int[] prices) {
// write code here
int n = prices.length;
//n dp[i][j][0] 前i天还可以交易k次 并且当前未持有股票的最大收益
int dp[][][] = new int[n + 1][3][2];
for (int i = 0; i <= n; i++) {
for (int j = 2; j >= 0; j--) {
if (i == 0) {
dp[0][j][0] = 0;
dp[0][j][1] = Integer.MIN_VALUE;
}
if (j == 0) {
dp[i][0][0] = 0;
dp[i][0][1] = Integer.MIN_VALUE;
} else {
if (i == 0) {
dp[0][j][0] = 0;
dp[0][j][1] = Integer.MIN_VALUE;
} else {
//当天卖出
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i-1]);
//当天买入
dp[i][j][1] = Math.max(dp[i - 1][j][1],
dp[i - 1][j - 1][0] - prices[i-1]);
}
}
}
}
return dp[n][2][0];
}
}
有冷冻期
如卖出一次得1天后才能再买入
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+p[i]);
//第i天持有 前i-1天持有 , 前i-2天未持有即买入(冷冻期一天), 记录买入消耗
dp[i][k][1] = max(dp[i-1][k][1],dp[i-2][k-1][0]-p[i]);
有卖出手续费
//第i天未持有 前i-1天未持有(不操作),前i-1天持有即卖出 需要记录卖出的收益
dp[i][k][0] = max(dp[i-1][k][0],dp[i-1][k][1]+p[i]-fee);
//第i天持有 前i-1天持有 , 前i-2天未持有即买入(冷冻期一天), 记录买入消耗
dp[i][k][1] = max(dp[i-1][k][1],dp[i-2][k-1][0]-p[i]);
区间动规
堆石头
每次任选2堆石子合并成新的一堆,合并的费用为新的一堆石子数。试设计一个算法,计算出将n堆石子合并成一堆的最小总费用。
- 先计算前缀和数组,p[i]表示前i堆堆叠后的费用和。
- f[i][j] 代表第i~j堆石子堆叠为一堆后的费用,那么上一步可能 是f[i][k]+f[k+1][j]+p[j]-p[i-1] k(i~k)
f[i][j] = Min(f[i][k]+f[k+1][j]+p[j]-p[i-1],f[i][j]),k(i~k)
扎气球
有n个气球,编号为0到n-1,每个气球都有一个分数,存在nums数组中。每次吹气球i可以得到的分数为 nums[left] * nums[i] * nums[right],left和right分别表示i气球相邻的两个气球。当i气球被吹爆后,其左右两气球即为相邻。要求吹爆所有气球,得到最多的分数。
- 在原有的气球基础上在最右和最左添加分数为1的气球,且不能扎破保证在最后的一个气球扎破时候能方便计算分数。
- f[i][j] 代表i-j个气球的(最后i和j不能扎破)区间中扎破第k个气球(是i-j中最后一个扎破的气球)那么f[i][j] = Max(f[i][k]+f[k][j]+nums[i]*nums[k]*nums[j],f[i][j]) k(i+1~j-1).
- 子问题就是 (i-k)和(k-j)区间中的扎气球求最大分数。k将区间划分两个子区间。
丢鸡蛋
给定N层楼,k个鸡蛋,问最坏情况下最少扔多少鸡蛋可以测出F楼层(大于F鸡蛋摔碎,小于不会)
什么叫做「最坏情况」下,鸡蛋破碎一定发生在搜索区间穷尽时.
若是没有鸡蛋个数限制,比如10层1层层测试那就最坏在10层不破碎,最多九个。这个看扔的策略,比如二分扔,最多log10+1 = 4,所以这时问最好的扔鸡蛋策略。
当有鸡蛋限制时,该怎么办扔?
比如100层,两鸡蛋一个二分碎啦,剩下二分1~50,若是结果24,那就刚好碎啦,还没测试出来,那就只能线性搜索24次,最坏情况49次。
若是按先10分的探测,最多10次测出在90~100之间,剩下一个线性探测,探测10次,此时就只需要20次,次数减少了。
所以如果只有一个鸡蛋那就只能线性探测,才能精准无误的探测到目标楼层,那子问题就是前一个鸡蛋怎么选择划分好这个区间(最后一个鸡蛋测试)让整体的测试次数最少。
递归:如果有i个鸡蛋在测n层楼,选择k层,若是碎了,接下来i-1个测k-1层楼,没碎就是i个鸡蛋测试n-k层的楼。
dfs(int k,int n){
if(k==1) return n;
if(k==0) return 0;
int res = 0;
for(int i=1;i<=n;i++){
res = Math.max(res, Math.min(dfs(k-1,i-1),dfs(k,n-i))+1);
}
return res;
}
dp优化
dp[n][k]
dfs(int k,int n){
if(k==1) return n;
if(k==0) return 0;
if(dp[k][n]!=0) return dp[k][n];
int res = 0;
for(int i=1;i<=n;i++){
res = Math.max(res, Math.min(dfs(k-1,i-1),dfs(k,n-i))+1);
}
dp[k][n] = res;
return res;
}
背包
01 – 物品选/不选
完全 – 物品数量无限
多重 – 物品数量k
刚好装满时最大价值与直接最大价值的区别在于base case初始化的不同!
字符串匹配

dp[i][j]代表前s前i哥和p前j哥字符是否匹配的问题:
- 若s[i] == s[j]; dp[i][j] |= dp[i-1][j-1]
- 若p[j] == ‘*’; dp[i][j] |= dp[i-1][j]; 若s[i]==p[j-1] dp[i][j] |= dp[i-1][j]
- 若p[j]==‘.’; dp[i][j] |= dp[i-1][j-1]
称砝码
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-FARATNsw-1690390210181)(https://s2.loli.net/2022/07/16/6Q2UsRWjP1NdC9S.png)]
dp[i][j] 表示前i中砝码能否称重j重量。
import java.util.*;
public class Main {
public static void main(String s[]) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m[] = new int[n];
int x[] = new int[n];
int sum = 0;
for (int i = 0; i < n; i++) {
m[i] = in.nextInt();
}
for (int i = 0; i < n; i++) {
x[i] = in.nextInt();
sum+=m[i]*x[i];
}
boolean dp[][] = new boolean[n][sum+1];
int t = m[0]*x[0];
int l=0;
while(l<=x[0]){
dp[0][m[0]*l]=true;
l++;
}
for(int i=1;i<n;i++){
dp[i][0]=true;
for(int j=1;j<=sum;j++){
//第i种不用
dp[i][j] |= dp[i-1][j];
//直接跳过
if(dp[i][j]) continue;
for(int k=1;k<=x[i];k++){
if(j-k*m[i]>=0) dp[i][j] |= dp[i-1][j-k*m[i]];
if(dp[i][j]) break;
}
}
}
int count =0;
for(int i=0;i<=sum;i++){
for(int j=0;j<n;j++){
if(dp[j][i]) {
count++;
break;
}
}
}
System.out.println(count);
}
}
时间复杂度O(N3),空间复杂度O(n*sum)。
优化压缩一维
import java.util.*;
public class Main {
public static void main(String s[]) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int m[] = new int[n];
int x[] = new int[n];
int sum = 0;
for (int i = 0; i < n; i++) {
m[i] = in.nextInt();
}
for (int i = 0; i < n; i++) {
x[i] = in.nextInt();
sum += m[i] * x[i];
}
boolean dp[] = new boolean [sum + 1];
// System.out.println(dp[sum]);
dp[0] = true;
//前i种砝码,前j个能否达到指定重量
for (int i = 0; i < n; i++) {
for (int j = 1; j <= x[i]; j++) {
//保证使用指定的数量j 能否达到k重量
for (int k = sum; k >=m[i]; k--) {
if(dp[k-m[i]]) dp[k] = true;
}
}
}
int count = 0;
for (int i = 0; i <= sum; i++) {
// if(dp[i]) System.out.println(i+" "+dp[i]);
if (dp[i]) count++;
}
System.out.println(count);
}
}
另外一种思路,如4-5个,6-7个 一个set维护当前能达到的重量数值,一次加入一个重量(限制加入个数),与现有重量组合,重新计算容量,set去重。
编辑距离
初始化dp[0][0]表示的是字符串a和b的空字符串编辑距离为0,dp[0][j] = j;这时为了更好的比较像 a , cdfsa这样的情况。
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
// import java.lang.Math;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String A = br.readLine();
String B = br.readLine();
char [] a = A.toCharArray();
char [] b= B.toCharArray();
int dp [][] = new int[a.length+1][b.length+1];
for(int i=0;i<=a.length;i++)
Arrays.fill(dp[i],Math.max(a.length,b.length));
dp[0][0] = 0;
for(int i=0;i<=a.length;i++){
dp[i][0] = i;
}
for(int i=0;i<=b.length;i++){
dp[0][i] = i;
}
for(int i=1;i<=a.length;i++){
for(int j=1;j<=b.length;j++){
if(a[i-1]==b[j-1]) {
dp[i][j] = Math.min(dp[i-1][j-1],dp[i][j]);
//b 插入一个字符
// if(i>=2) dp[i][j] = Math.min(dp[i-2][j-1]+1,dp[i][j]);
// //a 插入一个字符
// if(j>=2) dp[i][j] = Math.min(dp[i-1][j-2]+1,dp[i][j]);
}
else {
//不等 删除一个 和插入类似
dp[i][j] = Math.min(dp[i-1][j]+1,dp[i][j]);
dp[i][j] = Math.min(dp[i][j-1]+1,dp[i][j]);
// 替换 或者 插入
// 如 abcd acd b与c比较 往ac之间插入b
dp[i][j] = Math.min(dp[i-1][j-1]+1,dp[i][j]);
}
//System.out.println(i+" "+j+" "+dp[i][j]);
}
}
System.out.println(dp[a.length][b.length]);
}
}
二维数组求最大正方形

思路:dp[i]][j] 表示以i,j作为右下角的拓展最大正方形宽,所以子问题是左上角,上方,左方拓展正方形的最小的宽。
dp[i][j]=min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1;
分糖果问题

思路:相当于求解递增序列长度,需两个方向上。 dp记录,两次dp,从左到右,从右到左,如果上一个分值比当前小,那么久 dp[i] = dp[i-1]+1;否则就为1.两次遍历完后,dpl[i] dpr[i] 中取最大值作为其分的糖果树,这就综合考虑从左向右和从右向左的递增性质。
import java.util.*;
public class Solution {
/**
* pick candy
* @param arr int整型一维数组 the array
* @return int整型
*/
public int candy (int[] arr) {
// write code here
int dpl[] = new int[arr.length];
int dpr[] = new int[arr.length];
for (int i = 0; i < arr.length; i++) {
if (i == 0) dpl[i] = 1;
else {
if (arr[i] > arr[i - 1]) dpl[i] = dpl[i - 1] + 1;
else if (arr[i] == arr[i - 1]) dpl[i] = 1;
else dpl[i] = 1;
}
}
for (int i = arr.length-1; i>=0; i--) {
if (i == arr.length-1) dpr[i] = 1;
else {
if (arr[i] > arr[i + 1]) dpr[i] = dpr[i +1] + 1;
else if (arr[i] == arr[i + 1]) dpr[i] = 1;
else dpr[i] = 1;
}
}
int count = 0;
for(int i=0;i<arr.length;i++){
count+= Math.max(dpl[i],dpr[i]);
}
return count;
}
}
贪心
区间覆盖
画图,找规律。
去除覆盖区间
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Vj9uMBAN-1690390210182)(https://s2.loli.net/2022/07/16/oSCmn9ukPsl3Zzp.png)]
思路:求被覆盖区间的数量。按照start升序排序,那么后一个区间[li,ri]。是否覆盖只要看前面的区间中 最大 rmax >= ri 。满足那区间[li,ri]一定被覆盖,按照start升序排序在按end降序排序,方便 在start相同的情况下,第一个就是最大的右边界的区间,这时只要判断其右边界情况。
start,end第一个区间,遍历区间[li,ri]。
-
如果相同li在start,end之间,ri是否被覆盖。
-
若ri> end 那就没有覆盖,但是可以更新end = 当前ri,因为在这之前一定不存在比li还起始早的区间没有遍历,后面遍历的区间lj一定大于等于li,所以后面遍历的只要看是不是第三种没交集(不会被覆盖)或者lj<=end(那么久会被覆盖)。
-
没有交集,更新start,end。
class Solution {
public int removeCoveredIntervals(int[][]intvs) {
//按照起点升序,终点降序
Arrays.sort(intvs,(o1,o2)->{
if(o1[0]==o2[0]) return o2[1] - o1[1];
return o1[0]-o2[0];
});
int count = 0;
int left =intvs[0][0],right = intvs[0][1];
for(int i=1;i<intvs.length;i++){
//如果覆盖
if(left <= intvs[i][0] && right >= intvs[i][1]){
count++;
}
//有交集那就合并区间
else if(right >= intvs[i][0] && right <= intvs[i][1]){
right = intvs[i][1];
}
//无交集 更新 left right 因为排序,之前不会还有比intvs[i][0] 小的
else if(right <= intvs[i][0]){
left = intvs[i][0];
right = intvs[i][1];
}
}
return intvs.length - count;
}
}
区间交集
主持人调度
活动安排
给定各个活动的开始结束时间,要求最大活动数量,无交集的最大活动安排。
import java.util.ArrayList;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
//创建一个集合存储数据
List<Node> xD = new ArrayList<Node>();
Node node;
for (int i = 0; i < n; i++) {
//数据类型的起始值
int a = scanner.nextInt();
int b = scanner.nextInt();
node = new Node(a, b);
//将活动对应的起始和结束时间加入集合
xD.add(node);
}
//对活动时间进行排序,按照末尾时间从小到大的标准
Collections.sort(xD, (o1, o2)-> {
return o1.end - o2.end;
});
int begin = 0, count = 0;
for (int i = 0; i < n; i++) {
//当当前的起始值大于上一个活动的结束值时,符合要求
if (xD.get(i).start >= begin) {
//更新begin的值
begin = xD.get(i).end;
count++;
}
}
System.out.println(count);
}
}
//节点类
class Node {
//该数据类型包含一个起始值,一个结束值,一个标记,
int start;
int end;
public Node(int start, int end) {
// TODO Auto-generated constructor stub
this.start = start;
this.end = end;
}
}