目录
多源BFS
矩阵距离
最小步数模型
魔板
八数码
双端队列广搜
电路维修
双向广搜
字串变换
A*
第K短路
多源BFS
单源BFS是求一个点到起点的最短距离
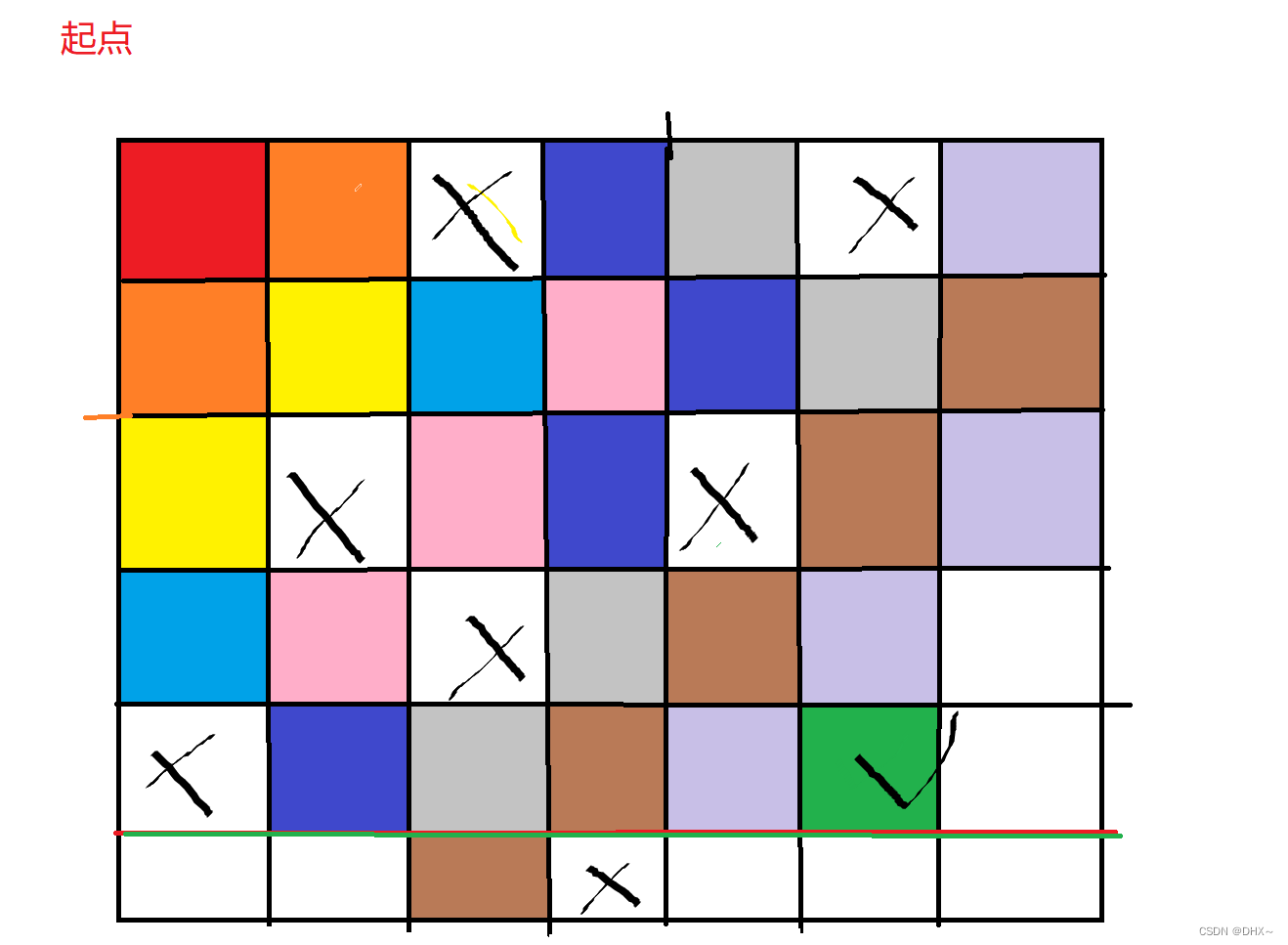
多源BFS是求有很多个起点,某一点到离它最近一个起点的距离
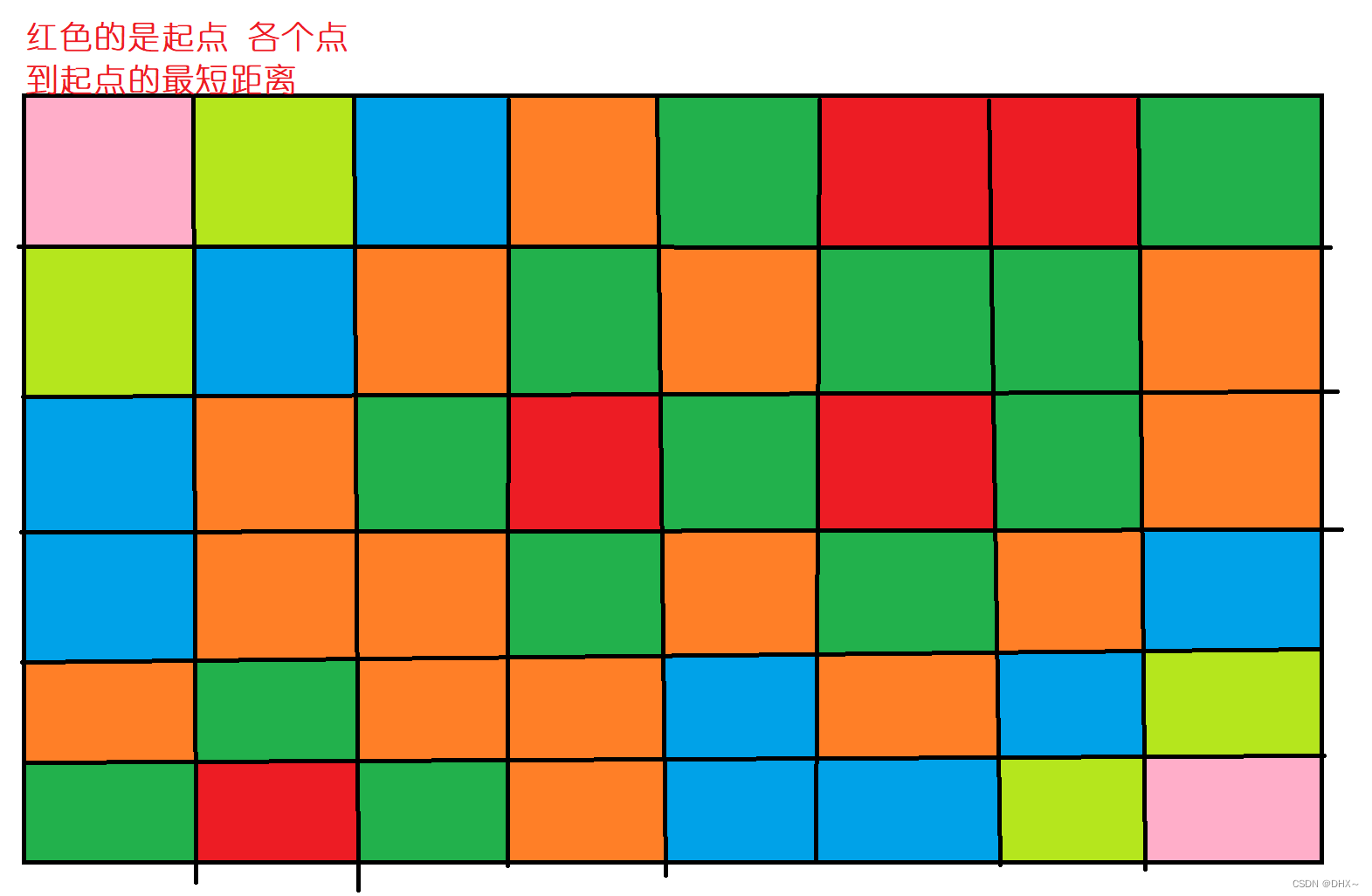
矩阵距离
给定一个 N 行M 列的 01矩阵 A,A[i][j] 与 A[k][l] 之间的曼哈顿距离定义为:
dist(A[i][j],A[k][l])=|i−k|+|j−l|
输出一个 N 行 M 列的整数矩阵 B,其中:
B[i][j]=min1≤x≤N,1≤y≤M,A[x][y]=1dist(A[i][j],A[x][y])
输入格式
第一行两个整数 N,M。
接下来一个 N 行 M 列的 01 矩阵,数字之间没有空格。
输出格式
一个 N行 M 列的矩阵 BB,相邻两个整数之间用一个空格隔开。
数据范围
1≤N,M≤1000
输入样例:
3 4
0001
0011
0110
输出样例:
3 2 1 0
2 1 0 0
1 0 0 1
#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>
#define x first
#define y second
using namespace std;
const int N=1010;
typedef pair<int,int>PII;
char g[N][N];
int dist[N][N];
int n,m;
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
void bfs()
{
memset(dist,-1,sizeof dist);//只改变一次 选一个特殊值就好
queue<PII>q;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
if(g[i][j]=='1')
{
dist[i][j]=0;
q.push({i,j});
}
}
}
while(q.size())
{
PII t=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int xx=t.x+dx[i],yy=t.y+dy[i];
if(xx<1||xx>n||yy<1||yy>m) continue;
if(dist[xx][yy]!=-1) continue;//值以及被修改过 就不修改了
dist[xx][yy]=dist[t.x][t.y]+1;
q.push({xx,yy});
}
}
}
int main()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++) cin>>g[i][j];
bfs();
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
cout<<dist[i][j]<<" ";
}
cout<<endl;
}
return 0;
}最小步数模型
魔板
Rubik 先生在发明了风靡全球的魔方之后,又发明了它的二维版本——魔板。
这是一张有 8 个大小相同的格子的魔板:
1 2 3 4
8 7 6 5
我们知道魔板的每一个方格都有一种颜色。
这 8 种颜色用前 8 个正整数来表示。
可以用颜色的序列来表示一种魔板状态,规定从魔板的左上角开始,沿顺时针方向依次取出整数,构成一个颜色序列。
对于上图的魔板状态,我们用序列 (1,2,3,4,5,6,7,8) 来表示,这是基本状态。
这里提供三种基本操作,分别用大写字母 A,B,C 来表示(可以通过这些操作改变魔板的状态):
A:交换上下两行;
B:将最右边的一列插入到最左边;
C:魔板中央对的4个数作顺时针旋转。
下面是对基本状态进行操作的示范:
A:
8 7 6 5
1 2 3 4
B:
4 1 2 3
5 8 7 6
C:
1 7 2 4
8 6 3 5
对于每种可能的状态,这三种基本操作都可以使用。
你要编程计算用最少的基本操作完成基本状态到特殊状态的转换,输出基本操作序列。
注意:数据保证一定有解。
输入格式
输入仅一行,包括 8 个整数,用空格分开,表示目标状态。
输出格式
输出文件的第一行包括一个整数,表示最短操作序列的长度。
如果操作序列的长度大于0,则在第二行输出字典序最小的操作序列。
数据范围
输入数据中的所有数字均为 1 到 8 之间的整数。
输入样例:
2 6 8 4 5 7 3 1
输出样例:
7
BCABCCB
#include<iostream>
#include<algorithm>
#include<queue>
#include<unordered_map>
#include<cstring>
#define x first
#define y second
using namespace std;
unordered_map<string,int>dist;
unordered_map<string,pair<char,string>>pre;//存储前驱
queue<string>q;
//直接用下标去改变
string get(string s,int op)
{
string res;
if(op==0)res=s,reverse(res.begin(),res.end());
if(op==1)res={s[3],s[0],s[1],s[2],s[5],s[6],s[7],s[4]};
if(op==2)res={s[0],s[6],s[1],s[3],s[4],s[2],s[5],s[7]};
return res;
}
int bfs(string start,string end)
{
if(start==end) return 0;
q.push(start);
dist[start]=0;
while(q.size())
{
string t=q.front();
q.pop();
for(int i=0;i<3;i++)
{
string x=get(t,i);
//count 在序列中统计某个值出现的次数
if(!dist.count(x))
{
dist[x]=dist[t]+1;
pre[x]={'A'+i,t};
q.push(x);
if(x==end) return dist[x];
}
}
}
}
int main()
{
string start,end;
for(int i=0;i<8;i++)
{
int x;cin>>x;
end+=char(x+'0');
}
start="12345678";
int num=bfs(start,end);
cout<<num<<endl;
string s;
while(start!=end)
{
s+=pre[end].x;
end=pre[end].y;
}
reverse(s.begin(),s.end());
if(num>0) cout<<s;
return 0;
}#include <cstring>
#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;
char g[2][4];
unordered_map<string, pair<char, string>> pre;
unordered_map<string, int> dist;
void set(string state)
{
for (int i = 0; i < 4; i ++ ) g[0][i] = state[i];
for (int i = 7, j = 0; j < 4; i --, j ++ ) g[1][j] = state[i];
}
string get()
{
string res;
for (int i = 0; i < 4; i ++ ) res += g[0][i];
for (int i = 3; i >= 0; i -- ) res += g[1][i];
return res;
}
string move0(string state)
{
set(state);
for (int i = 0; i < 4; i ++ ) swap(g[0][i], g[1][i]);
return get();
}
string move1(string state)
{
set(state);
int v0 = g[0][3], v1 = g[1][3];
for (int i = 3; i > 0; i -- )
{
g[0][i] = g[0][i - 1];
g[1][i] = g[1][i - 1];
}
g[0][0] = v0, g[1][0] = v1;
return get();
}
string move2(string state)
{
set(state);
int v = g[0][1];
g[0][1] = g[1][1];
g[1][1] = g[1][2];
g[1][2] = g[0][2];
g[0][2] = v;
return get();
}
int bfs(string start, string end)
{
if (start == end) return 0;
queue<string> q;
q.push(start);
dist[start] = 0;
while (!q.empty())
{
auto t = q.front();
q.pop();
string m[3];
m[0] = move0(t);
m[1] = move1(t);
m[2] = move2(t);
for (int i = 0; i < 3; i ++ )
if (!dist.count(m[i]))
{
dist[m[i]] = dist[t] + 1;
pre[m[i]] = {'A' + i, t};
q.push(m[i]);
if (m[i] == end) return dist[end];
}
}
return -1;
}
int main()
{
int x;
string start, end;
for (int i = 0; i < 8; i ++ )
{
cin >> x;
end += char(x + '0');
}
for (int i = 1; i <= 8; i ++ ) start += char('0' + i);
int step = bfs(start, end);
cout << step << endl;
string res;
while (end != start)
{
res += pre[end].first;
end = pre[end].second;
}
reverse(res.begin(), res.end());
if (step > 0) cout << res << endl;
return 0;
}
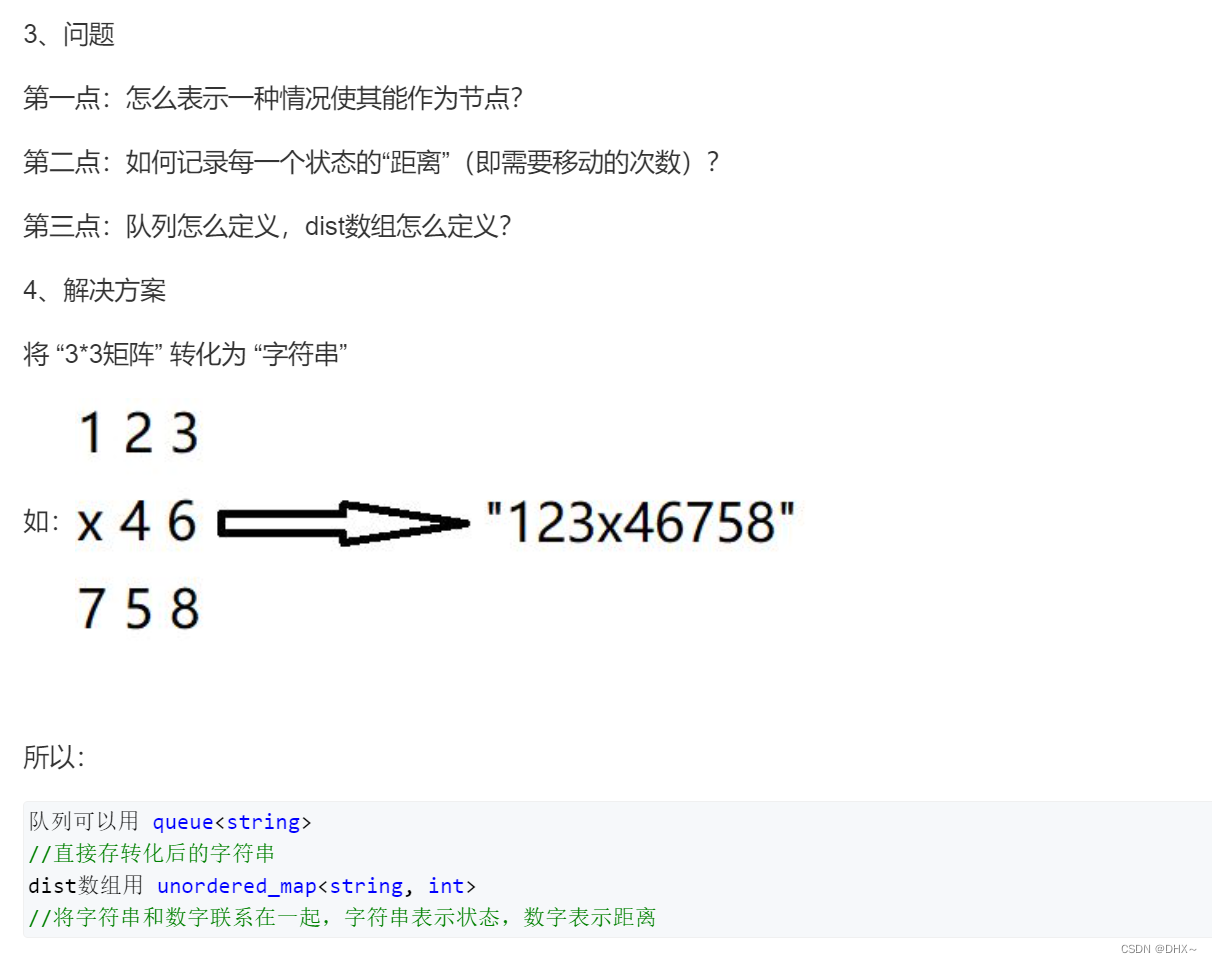
八数码
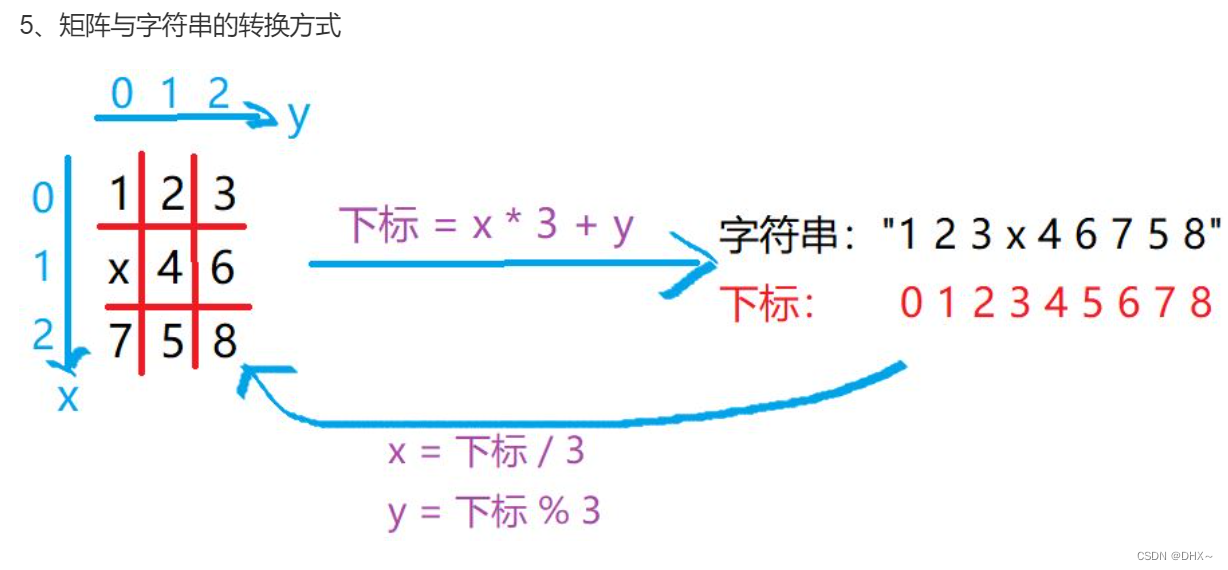
在一个 3×3 的网格中,1∼8 这 8 个数字和一个 x 恰好不重不漏地分布在这 3×3 的网格中。
例如:
1 2 3
x 4 6
7 5 8
在游戏过程中,可以把 x 与其上、下、左、右四个方向之一的数字交换(如果存在)。
我们的目的是通过交换,使得网格变为如下排列(称为正确排列):
1 2 3
4 5 6
7 8 x
例如,示例中图形就可以通过让 x 先后与右、下、右三个方向的数字交换成功得到正确排列。
交换过程如下:
1 2 3 1 2 3 1 2 3 1 2 3
x 4 6 4 x 6 4 5 6 4 5 6
7 5 8 7 5 8 7 x 8 7 8 x
现在,给你一个初始网格,请你求出得到正确排列至少需要进行多少次交换。
输入格式
输入占一行,将 3×3的初始网格描绘出来。
例如,如果初始网格如下所示:
1 2 3
x 4 6
7 5 8
则输入为:1 2 3 x 4 6 7 5 8
输出格式
输出占一行,包含一个整数,表示最少交换次数。
如果不存在解决方案,则输出 −1。
输入样例:
2 3 4 1 5 x 7 6 8
输出样例
19 

#include<iostream>
#include<cstring>
#include<unordered_map>
#include<algorithm>
#include<cstring>
#include<queue>
using namespace std;
unordered_map<string,int>dist;
queue<string>q;
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
int bfs(string start)
{
q.push(start);
dist[start]=0;
while(q.size())
{
string t=q.front();
q.pop();
int distance=dist[t];//保存起来 方便更新元素
if(t=="12345678x") return dist[t];
int k=t.find('x');//返回x在队列中的下标
int x1=k/3,y1=k%3;//将其转化为 3*3 矩阵中的坐标
for(int i=0;i<4;i++)
{
int xx=x1+dx[i],yy=y1+dy[i];
if(xx>=0&&xx<3&&yy>=0&&yy<3)//没有越界
{
swap(t[k],t[xx*3+yy]);//交换在队列的下标元素
if(!dist[t])//没有存储过 最新的更新
{
dist[t]=distance+1;
q.push(t);
}
swap(t[k],t[xx*3+yy]);//交换回去方便后面的交换是在最初的位置上交换
}
}
}
return -1;//没有找到返回-1
}
int main()
{
string start;
for(int i=0;i<9;i++)
{
char c;cin>>c;
start+=c;
}
int num=bfs(start);
cout<<num<<endl;
}双端队列广搜
电路维修
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。
翰翰的家里有一辆飞行车。
有一天飞行车的电路板突然出现了故障,导致无法启动。
电路板的整体结构是一个 RR 行 CC 列的网格(R,C≤500R,C≤500),如下图所示。
达达是来自异世界的魔女,她在漫无目的地四处漂流的时候,遇到了善良的少女翰翰,从而被收留在地球上。
翰翰的家里有一辆飞行车。
有一天飞行车的电路板突然出现了故障,导致无法启动。
电路板的整体结构是一个 R 行 C 列的网格(R,C≤500),如下图所示。
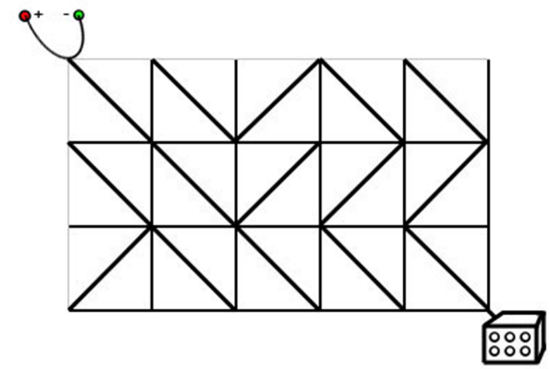
每个格点都是电线的接点,每个格子都包含一个电子元件。
电子元件的主要部分是一个可旋转的、连接一条对角线上的两个接点的短电缆。
在旋转之后,它就可以连接另一条对角线的两个接点。
电路板左上角的接点接入直流电源,右下角的接点接入飞行车的发动装置。
达达发现因为某些元件的方向不小心发生了改变,电路板可能处于断路的状态。
她准备通过计算,旋转最少数量的元件,使电源与发动装置通过若干条短缆相连。
不过,电路的规模实在是太大了,达达并不擅长编程,希望你能够帮她解决这个问题。
注意:只能走斜向的线段,水平和竖直线段不能走。
输入格式
输入文件包含多组测试数据。
第一行包含一个整数 T,表示测试数据的数目。
对于每组测试数据,第一行包含正整数 R 和 C,表示电路板的行数和列数。
之后 R 行,每行 C 个字符,字符是"/"和"\"中的一个,表示标准件的方向。
输出格式
对于每组测试数据,在单独的一行输出一个正整数,表示所需的最小旋转次数。
如果无论怎样都不能使得电源和发动机之间连通,输出 NO SOLUTION。
数据范围
1≤R,C≤500
1≤T≤5
输入样例:
1
3 5
\\/\\
\\///
/\\\\
输出样例:
1
样例解释
样例的输入对应于题目描述中的情况。
只需要按照下面的方式旋转标准件,就可以使得电源和发动机之间连通。
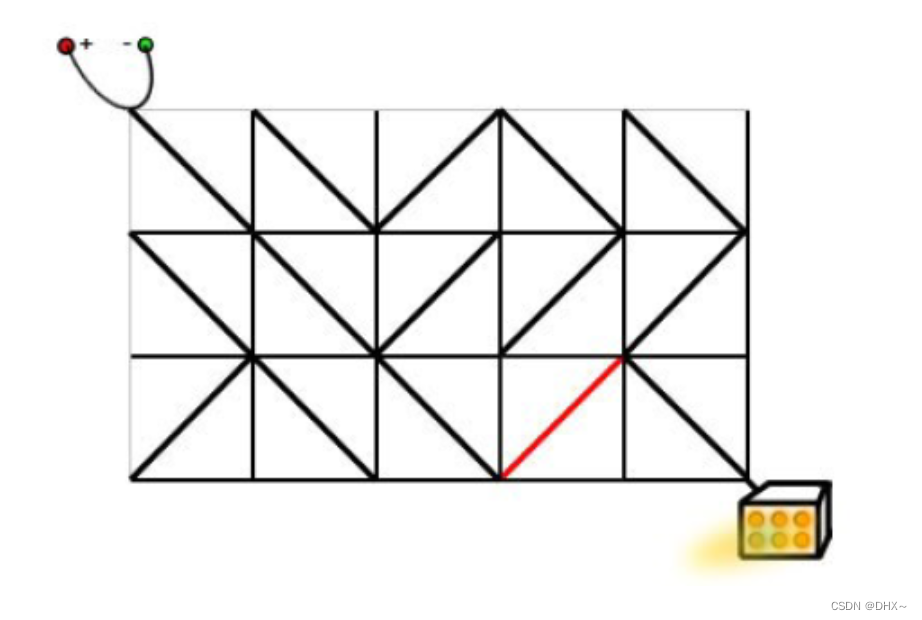

红点走不了 行数加列数是偶点可以走 奇点不可以走 它只能走斜线 故行数和列数要么同时加一 要么同时减一



#include<iostream>
#include<algorithm>
#include<deque>
#include<cstring>
#define x first
#define y second
using namespace std;
const int N=505;
typedef pair<int,int>PII;
char g[N][N];
bool st[N][N];
int dist[N][N];
int n,m;
int bfs()
{
int dx[]={-1,-1,1,1},dy[]={-1,1,1,-1};//方向
int idx[]={-1,-1,0,0},idy[]={-1,0,0,-1};//格子
char str[]={'\\','/','\\','/'};//四个格子对应的符号
memset(st,0,sizeof st);
memset(dist,0x3f,sizeof dist);
deque<PII>q;
q.push_back({0,0});
dist[0][0]=0;
while(q.size())
{
PII t=q.front();
q.pop_front();
int x1=t.x,y1=t.y;
if(x1==n&&y1==m) return dist[x1][y1];
if(st[x1][y1]) continue;
st[x1][y1]=true;
for(int i=0;i<4;i++)
{
int xx=x1+dx[i],yy=y1+dy[i];
if(xx<0||xx>n||yy<0||yy>m) continue;
int gx=x1+idx[i],gy=y1+idy[i];
int w=0;
if(g[gx][gy]!=str[i]) w=1;
int d=dist[x1][y1]+w;
if(d<=dist[xx][yy])
{
dist[xx][yy]=d;
if(!w)q.push_front({xx,yy});//边权为0 往对头插
else q.push_back({xx,yy});//边权为1 往队尾插
}
}
}
return -1;
}
int main()
{
int t;cin>>t;
while(t--)
{
cin>>n>>m;
for(int i=0;i<n;i++)
for(int j=0;j<m;j++) cin>>g[i][j];
if((n+m)%2!=0)printf("NO SOLUTION\n");
else
{
int num=bfs();
cout<<num<<endl;
}
}
return 0;
}双向广搜
字串变换
已知有两个字串 A, B 及一组字串变换的规则(至多 6 个规则):
A1→B1
A2→B2
…
规则的含义为:在 A 中的子串 A1 可以变换为 B1、A2 可以变换为 B2…。
例如:A=abcd B=xyz
变换规则为:
abc → xu ud → y y → yz
则此时,A 可以经过一系列的变换变为 B,其变换的过程为:
abcd → xud → xy →xyz
共进行了三次变换,使得 A 变换为 B。
注意,一次变换只能变换一个子串,例如 A=aa B=bb
变换规则为:
a →b
此时,不能将两个 a 在一步中全部转换为 b,而应当分两步完成。
输入格式
输入格式如下:
A B
A1 B1
A2 B2
… …
第一行是两个给定的字符串 A和 B。
接下来若干行,每行描述一组字串变换的规则。
所有字符串长度的上限为 20。
输出格式
若在 10 步(包含 10 步)以内能将 A 变换为 B ,则输出最少的变换步数;否则输出 NO ANSWER!。
输入样例:
abcd xyz
abc xu
ud y
y yz
输出样例:
3
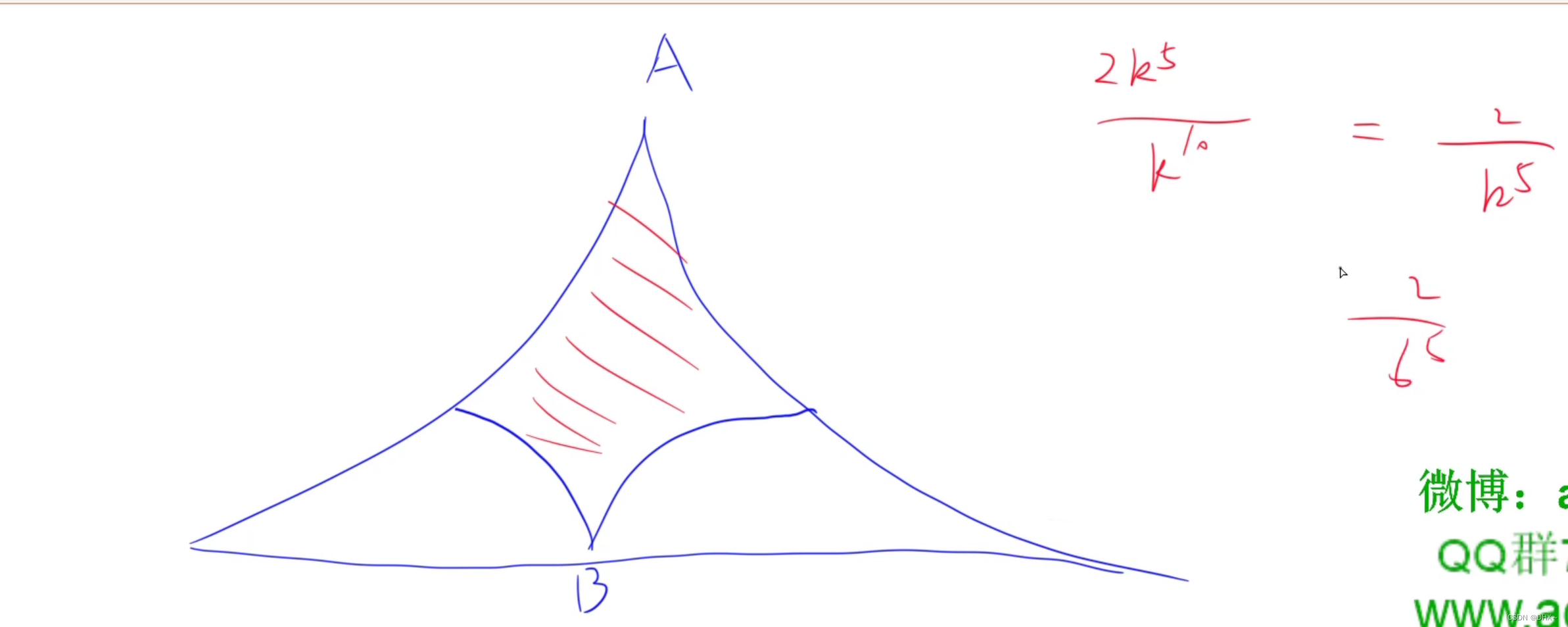
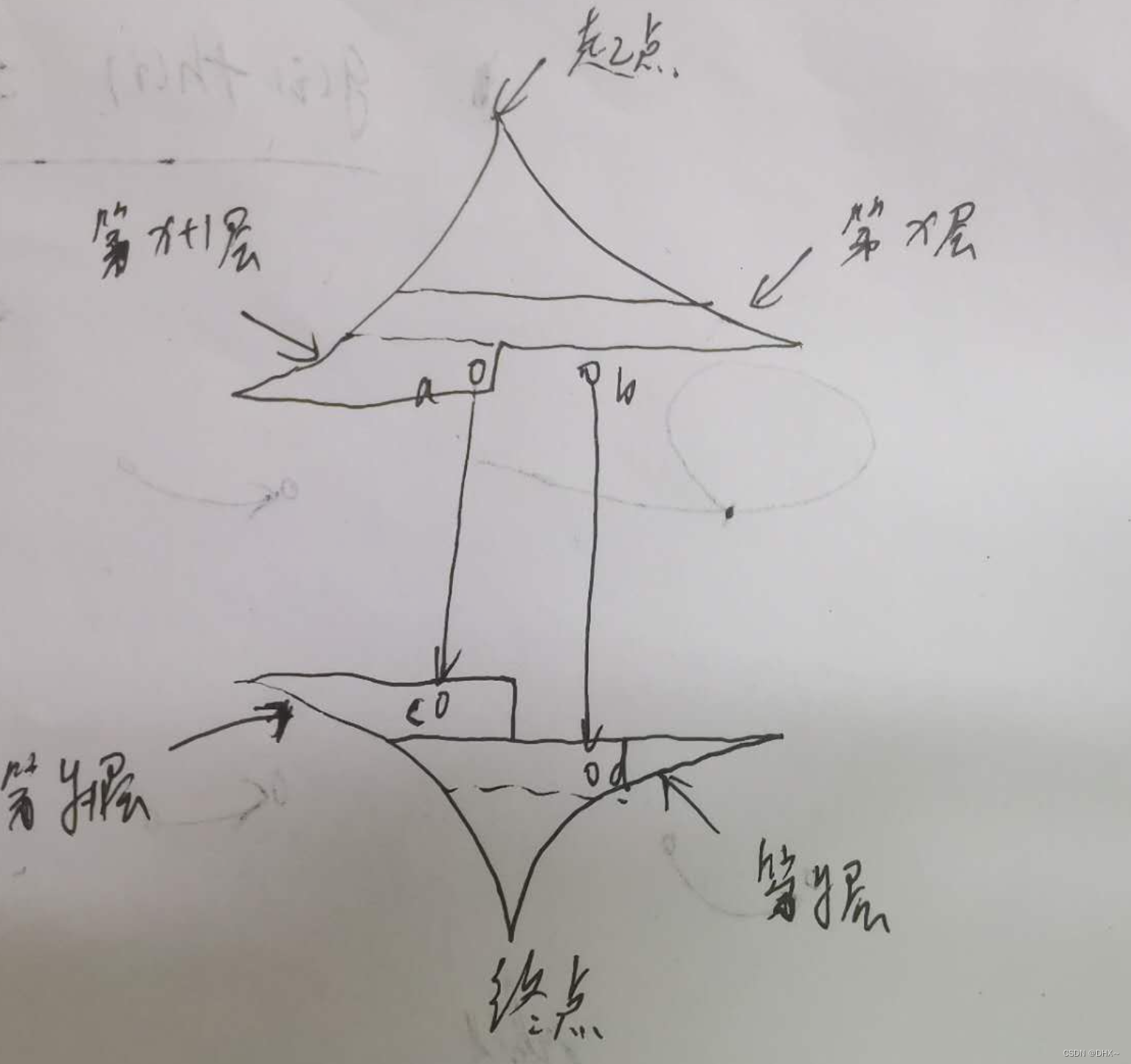
如上图,如果每次不是扩展完整一层,而是只扩展一个点。此时上面该扩展点 a 了,点 a 搜到了下半部分的点 c,此时算出的最短路长度是 x+1+y+1+1=x+y+3。但是最优解可能是后面还没扩展到的点 bb 和点 dd 之间的路径,这条路径的长度是 x+1+y+1=x+y+2。
#include<iostream>
#include<algorithm>
#include<queue>
#include<unordered_map>
#include<cstring>
using namespace std;
const int N=6;
string A,B;//字符串A 字符串B
string a[N],b[N];//存储变换规则
int n;
int extend(queue<string>&q,unordered_map<string,int>&da,unordered_map<string,int>&db,string a[N],string b[N])
{
int d=da[q.front()];
//必须遍历每一层 扩展跟队首同一层
while(q.size()&&da[q.front()]==d)
{
auto t=q.front();
q.pop();
//如果t这个字符串的一段= 规则,比如= xyz,才可以替换
for(int i=0;i<n;i++)
{
//遍历t
for(int j=0;j<t.size();j++)
{
if(t.substr(j,a[i].size())==a[i])
{
// 变换之后的结果state:前面不变的部分+ 变化的部分 + 后面不变的部分
// 比如abcd ,根据规则abc--> xu,变成 xud,这里的state就是xud
string r=t.substr(0,j)+b[i]+t.substr(j+a[i].size());
//在db中出现过 两个方向会师,返回最小步数
if(db.count(r)) return da[t]+db[r]+1;
// 如果该状态之前已扩展过,
if(da.count(r)) continue;
da[r]=da[t]+1;
q.push(r);
}
}
}
}
return 20;
}
// 从起点和终点来做bfs
int bfs()
{
if(A==B) return 0;
// 两个方向的队列
queue<string>qa,qb;
// qa从起点开始搜,qb从终点开始搜
unordered_map<string,int>da,db;
qa.push(A);qb.push(B);
// 起点A到起点的距离为0 终点B到终点B的距离为0
da[A]=0;db[B]=0;
int step=0;
// qa和qb都有值,说明可以扩展过来,否则说明是不相交的
while(qa.size()&&qb.size())
{
step++;
int t;
// 记录最小步数
// 哪个方向的队列的长度更小一些,空间更小一些,从该方向开始扩展,
// 时间复杂度比较平滑,否则有1个点会超时
if(qa.size()<qb.size()) t=extend(qa,da,db,a,b);
else t=extend(qb,db,da,b,a);
if(t<=10) return t;
//变换步数超过10则不成立
if(step>10) return -1;
}
// 如果不连通或者最小步数>10,则返回-1的数
return -1;
}
int main()
{
cin>>A>>B;
while(cin>>a[n]>>b[n]) n++;
int num=bfs();
if(num==-1) printf("NO ANSWER!\n");
else cout<<num<<endl;
return 0;
}A*
A*算法:边权可以是任意的 但是不能有负权回路 使用情景 有解使用它
最小距离只对终点成立 对于其中任意一点都不能成立

第K短路
给定一张 N 个点(编号 1,2…N),M 条边的有向图,求从起点 S 到终点 T 的第 K 短路的长度,路径允许重复经过点或边。
注意: 每条最短路中至少要包含一条边。
输入格式
第一行包含两个整数 N 和 M。
接下来 M 行,每行包含三个整数 A,B 和 L,表示点 A 与点 B 之间存在有向边,且边长为L。
最后一行包含三个整数 S,T 和 K,分别表示起点 S,终点 T 和第 K 短路。
输出格式
输出占一行,包含一个整数,表示第 K 短路的长度,如果第 K 短路不存在,则输出 −1。
数据范围
1≤S,T≤N≤1000
0≤M≤10^4,
1≤K≤1000,
1≤L≤100
输入样例:
2 2
1 2 5
2 1 4
1 2 2
输出样例:
14
#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>
#define x first
#define y second
using namespace std;
typedef pair<int, int> PII;
typedef pair<int, PII> PIII;
const int N = 1010, M = 200010;
int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];
void add(int h[], int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
void dijkstra()
{
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, T});
memset(dist, 0x3f, sizeof dist);
dist[T] = 0;
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.y;
if (st[ver]) continue;
st[ver] = true;
for (int i = rh[ver]; ~i; i = ne[i])
{
int j = e[i];
if (dist[j] > dist[ver] + w[i])
{
dist[j] = dist[ver] + w[i];
heap.push({dist[j], j});
}
}
}
}
int astar()
{
priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
heap.push({dist[S], {0, S}});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.y.y, distance = t.y.x;
cnt[ver] ++ ;
if (cnt[T] == K) return distance;
for (int i = h[ver]; ~i; i = ne[i])
{
int j = e[i];
if (cnt[j] < K)
heap.push({distance + w[i] + dist[j], {distance + w[i], j}});
}
}
return -1;
}
int main()
{
scanf("%d%d", &n, &m);
memset(h, -1, sizeof h);
memset(rh, -1, sizeof rh);
for (int i = 0; i < m; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(h, a, b, c);
add(rh, b, a, c);
}
scanf("%d%d%d", &S, &T, &K);
if (S == T) K ++ ;
dijkstra();
printf("%d\n", astar());
return 0;
}