1. 某核心企业需要在6个待选的零部件供应商中选择一个合作伙伴，各待选供应商有关数据如表1所列，试从中选择一个最优供应商(理想解法)

评价指标	产品质量	产品价格/元	地理位置/km	售后服务/h	技术水平	经济效益	供应能力/件	市场影响度	交货情况
1	0.83	326	21	3.2	0.2	0.15	250	0.23	0.87
2	0.9	295	38	2.4	0.25	0.2	180	0.15	0.95
3	0.99	340	25	2.2	0.12	0.14	300	0.27	0.99
4	0.92	287	19	2	0.33	0.09	200	0.3	0.89
5	0.87	310	27	0.9	0.2	0.15	150	0.18	0.82
6	0.95	303	10	1.7	0.09	0.17	175	0.26	0.94

效益型指标：产品质量、技术水平、经济效益、供应能力、市场影响度、交货情况

成本型指标：产品价格、地理位置、售后服务

供应商选择顺序：5>6>4>1>3>2（模型改进后的结果）[排序：465312]

根据理想解法求出的结果看出，供应商5优于其他供应商

模型评价： TOPSIS法的局限性：默认了所有指标的重要程度是相同的，即权重相同，但在实际问题中，不同的指标往往具有不同的权重大小。

模型改进：使用信息熵法对指标进行赋权法

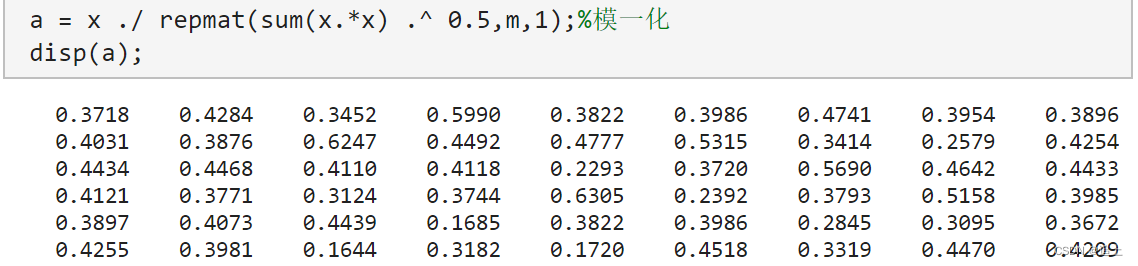
1. 对数据进行规范化的结果（模一化）

2. 由信息熵法确定权重

3. 得到带权重的矩阵

4. 正理想解和负理想解

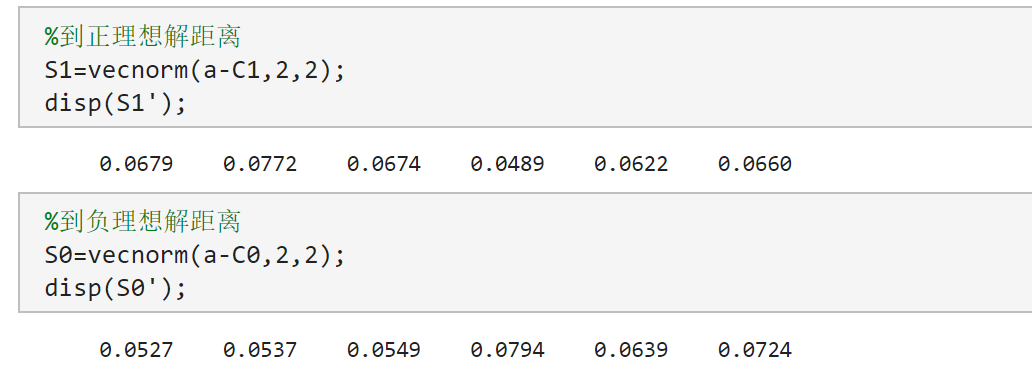
5. 到正理想解距离和到负理想解距离

6. 相对近似度

7. 优劣顺序
   

clc
clear

load matlab.mat
x = M;
[m,n] = size(x);

%无量纲化（模一化）
%a = x ./ sum(x);
a = x ./ repmat(sum(x.*x) .^ 0.5,m,1);%模一化
disp(a);

%信息熵
p=a./sum(a);
e=-sum(p.*log(p))/log(n);
g=1-e;
w=g/sum(g); %计算权重
a = a .* w;
disp(a);

%正理想解
C1 = max(a);
for i = 2:4
    C1(i)=min(a(:,i));
end
disp(C1);
%负理想解
C0 = min(a);
for i = 2:4
    C0(i)=max(a(:,i));
end
disp(C0);

%到正理想解距离
S1=vecnorm(a-C1,2,2);
disp(S1');
%到负理想解距离
S0=vecnorm(a-C0,2,2);
disp(S0');

f=S0'./(S1'+S0');
disp(f);
b = f ./ sum(f);
[sf,ind]=sort(b,'descend');%求排序结果
disp(ind);

2. 你已经去过几家主要的摩托车商店，基本确定将从三种车型中选购一种，你选择的标准主要有:价格、耗油量大小、舒适程度和外观美观情况。经反复思考比较，构造了它们之间的成对比较判断矩阵。

$A=\left[\begin{array}{cccc}1& 3& 7& 8\\ 1/3& 1& 5& 5\\ 1/7& 1/5& 1& 3\\ 1/8& 1/5& 1/3& 1\end{array}\right]$

三种车型(记为 a,b,c ) 关于价格、耗油量、舒适程度和外表美观情况的成对比较判断矩阵为

$\begin{array}{r}\left(价格\right)\\ \left[\begin{array}{ccc}1& 2& 3\\ 1/2& 1& 2\\ 1/3& 1/2& 1\end{array}\right]\end{array}$$\begin{array}{r}\left(耗油量\right)\\ \left[\begin{array}{ccc}1& 1/5& 1/2\\ 5& 1& 7\\ 2& 1/7& 1\end{array}\right]\end{array}$

$\begin{array}{r}\left(舒适程度\right)\\ \left[\begin{array}{ccc}1& 3& 5\\ 1/3& 1& 4\\ 1/5& 1/4& 1\end{array}\right]\end{array}$$\begin{array}{r}\left(外表\right)\\ \left[\begin{array}{ccc}1& 1/5& 3\\ 5& 1& 7\\ 1/3& 1/7& 1\end{array}\right]\end{array}$

(1) 根据上述矩阵可以看出四项标准在你心目中的比重是不同的，请按由重到轻顺序将它们排出。

(2) 哪辆车最便宜、哪辆车最省油、哪辆车最舒适、哪辆车最漂亮?

(3) 用层次分析法确定你对这三种车型的喜欢程度(用百分比表示)。

解：

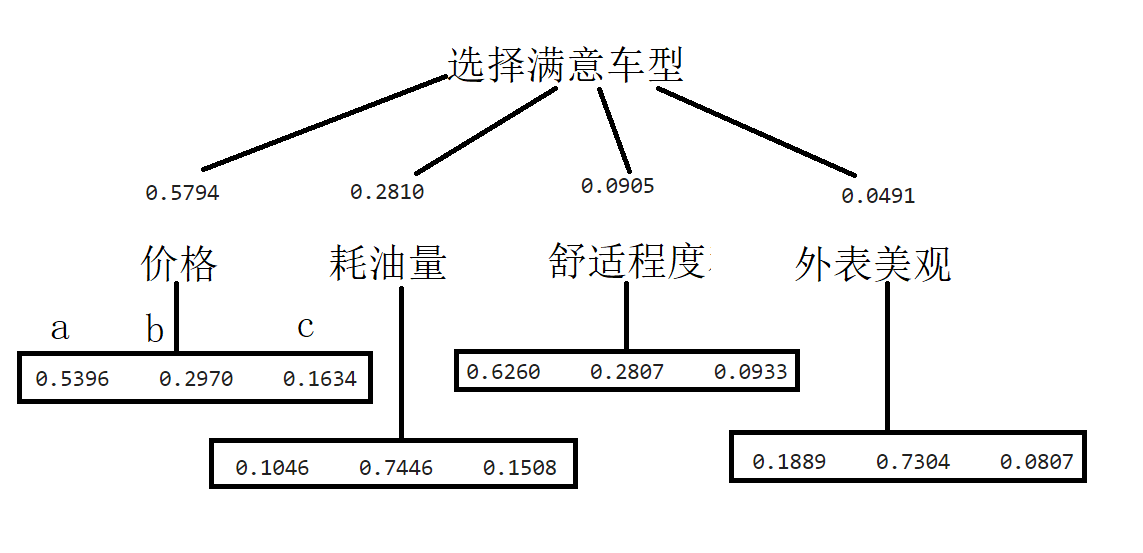
	价格	耗油量	舒适程度	外观
a	0.5396	0.1046	0.6260	0.1889
b	0.2970	0.7446	0.2807	0.7304
c	0.1634	0.1508	0.0933	0.0807
最大特征根	3.0092	3.1223	3.0867	3.0658
一致性指标	0.0046	0.0612	0.0433	0.0329

(1)

P_a= 0.5794 * 0.5396+0.2810 * 0.1046+0.0905 * 0.6260+0.0491 * 0.1889 = 0.4080

P_b= 0.5794 * 0.2970+0.2810 * 0.7446+0.0905 * 0.2807+0.0491 * 0.7304 = 0.4426

P_c= 0.5794 * 0.1634+0.2810 * 0.1508+0.0905 * 0.0933+0.0491 * 0.0807 = 0.1495

b>a>c

(2)

c车最便宜、a车最省油、a车最舒适、b车最漂亮

(3)

P_a+P_b+P_c=1

喜欢程度：

a车：40.8%

b车：44.26%

c车：14.95%

解析：

对于给出的每一个矩阵，都需要经过如下过程：

1. a矩阵归一化，得矩阵b
2. b矩阵按行求和,得矩阵c
3. c归一化,得矩阵d(此时得到的矩阵就是目标层的权值)
4. 对a矩阵进行赋值（a * d），得矩阵e
5. 对矩阵e进行归一化，得权向量x
6. 求矩阵的最大特征根y，sum(e./d)/n;
7. 求一致性指标z，(y - n) ./ (n-1);

function [x,y,z]= ccfx(a,n)
    b = a ./ sum(a);%归一化
    c = sum(b,2);%按行求和
    d = c ./ sum(c);
    e = a*d;
    x = e ./ sum(e);
    y = sum(e./d)/n;
    z = (y - n) ./ (n-1);
end

clc;
clear;

a = [1 3 7 8;1/3 1 5 5;1/7 1/5 1 3;1/8 1/5 1/3 1];

b1 = [1 2 3;1/2 1 2;1/3 1/2 1];
b2 = [1 1/5 1/2;5 1 7;2 1/7 1];
b3 = [1 3 5;1/3 1 4;1/5 1/4 1];
b4 = [1 1/5 3;5 1 7;1/3 1/7 1];

[w0,u0,ci0] = ccfx(a,4);
[w1,u1,ci1] = ccfx(b1,3);
[w2,u2,ci2] = ccfx(b2,3);
[w3,u3,ci3] = ccfx(b3,3);
[w4,u4,ci4] = ccfx(b4,3);

c1 = [w1,w2,w3,w4];%权向量
c2 = [u1,u2,u3,u4];%最大特征根
c3 = [ci1,ci2,ci3,ci4];%一致性指标CI

disp(w0');
disp(c1');
disp(c2);
disp(c3);