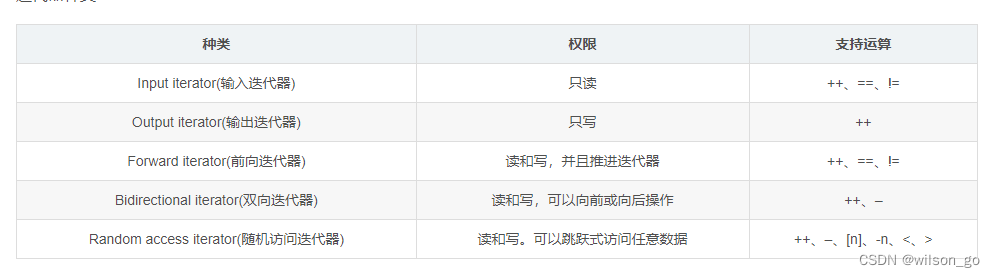
位运算
剑指 Offer II 003. 前 n 个数字二进制中 1 的个数
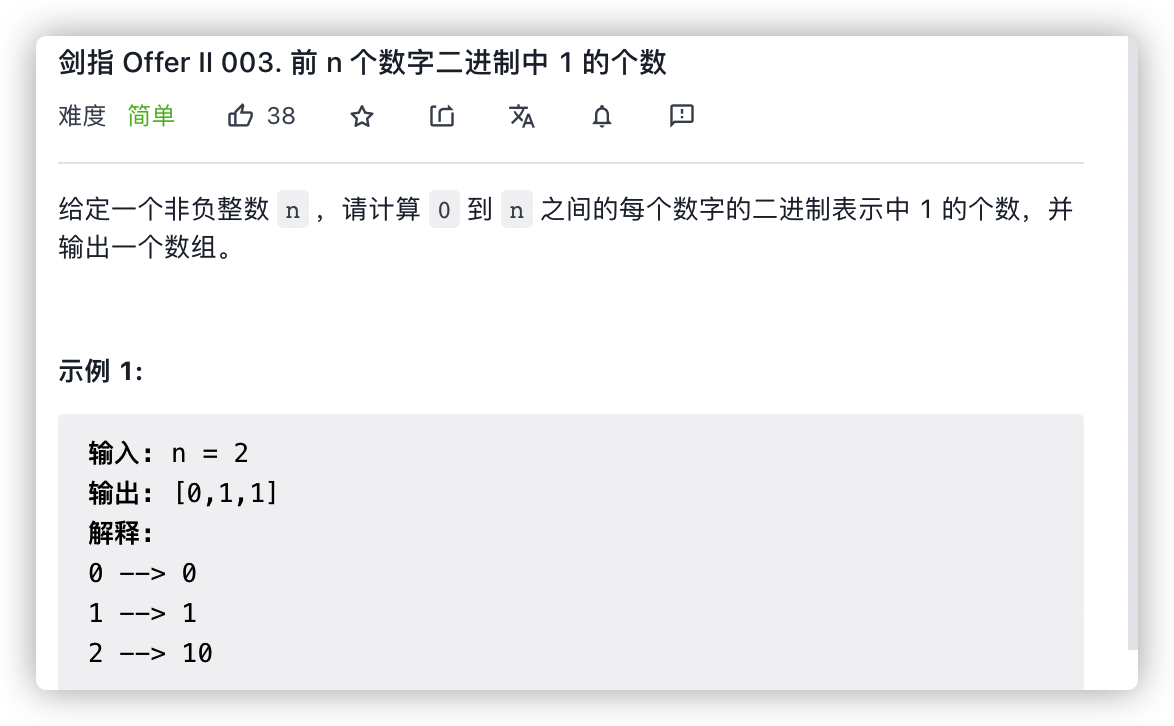
快速计算1比特数 x= x&(x-1)
将数字的最后一位变成0直到x=0,就可以计算出每一个数字中的1比特数。不过要求O(N)
- 动态规划
- 奇数:二进制表示中,奇数一定比前面那个偶数多一个 1,因为多的就是最低位的 1。
- 偶数:二进制表示中,偶数中 1 的个数一定和除以 2 之后的那个数一样多。因为最低位是 0,除以 2 就是右移一位,也就是把那个 0 抹掉而已,所以 1 的个数是不变的。
链接:
class Solution {
public int[] countBits(int n) {
int [] res = new int[n+1];
res[0]=0;
for(int i=1;i<=n;i++){
if(i%2==1) res[i]=res[i-1]+1;
else res[i] = res[i>>1];
}
return res;
}
}
剑指 Offer II 004. 只出现一次的数字
-
依次确定每一个二进制位
答案的第 i个二进制位就是数组中所有元素的第 i个二进制位之和除以3的余数。
class Solution {
public int singleNumber(int[] nums) {
//位运算,计算所有数值 某个位上之和,如果和为3的倍数那么 改为上要求的数值为0
//否则改位为1
int bitSum[] = new int[32];
for(int i=0;i<nums.length;i++){
int t = nums[i];
int j=0;
while(j<32&&t!=0){
//左移一位
if((t&1)==1) bitSum[j]++;
t>>=1;
j++;
}
}
int res =0;
for(int i=0;i<32;i++){
if(bitSum[i]%3!=0){
res|=1<<i;
}
}
System.out.println(bitSum[31]);
return res;
}
}
- 异或运算
算数三补1,逻辑双补0。
剑指 Offer 03. 数组中重复的数字

要求时间O(N),空间O(1) 注意条件数组长度n,数值0~n-1.
原地置换,将所有元素归位。
#include <iostream>
using namespace std;
int main() {
int nums [] = {1,4,3,2,2};
while(nums[nums[0]]!=nums[0]){
int t = nums[0];
nums[0] = nums[t];
nums[t] = t;
}
cout<<nums[0];
}
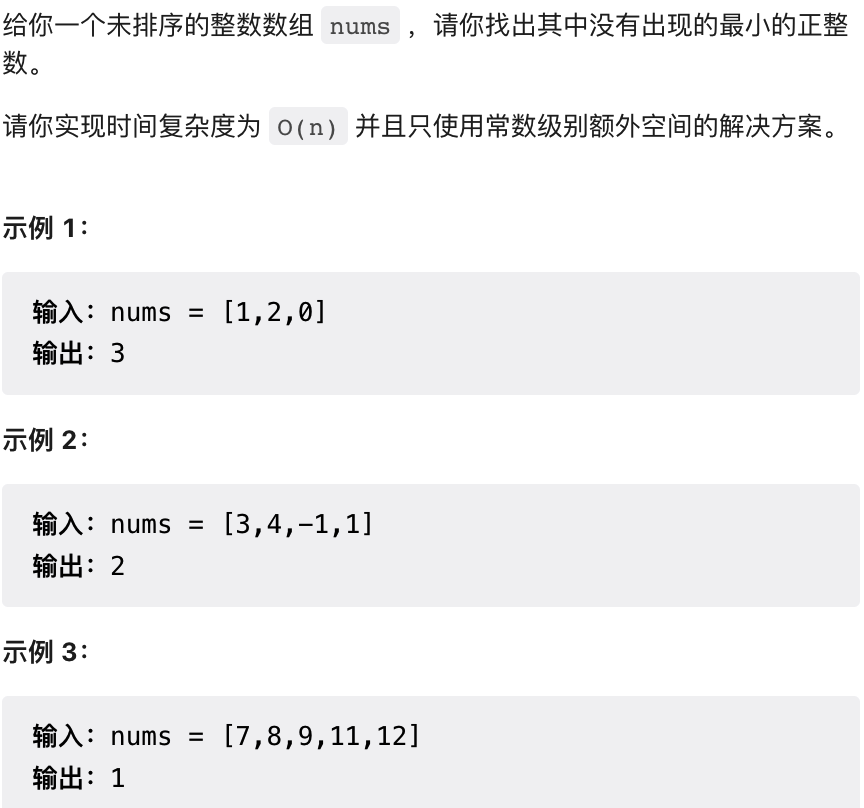
数组中首次缺失的数字
class Solution {
public int firstMissingPositive(int[] nums) {
//归位 将x 放入索引为 x-1的位置
// 缺失的数值一定在 1~len+1中
//遍历一遍 正数最小
// int min = Integer.MAX_VALUE;
// for(int i=0;i<nums.length;i++) if(nums[i]>0&&min>nums[i]) min = nums[i];
// [7,8,9,11,12] 长度为5 缺失的数值一定在 1~6之间,对于超过n+1的数直接忽略掉.
//
// for(int i=0;i<nums.length;i++) if(nums[i]>0) nums[i]-=min;
int len = nums.length;
for(int i=0;i<nums.length;i++){
while(nums[i]>0&&nums[i]<=len&&nums[nums[i]-1]!=nums[i]){
swap(nums,nums[i]-1,i);
}
// for(int j=0;j<nums.length;j++) System.out.print(nums[j]+" ");
}
// for(int i=0;i<nums.length;i++) System.out.print(nums[i]+" ");
for(int i=0;i<nums.length;i++){
if(nums[i]-1!=i) return i+1;
}
return len+1;
}
public void swap(int []nums,int i,int j){
nums[i] = nums[i]^nums[j];
nums[j] = nums[i]^nums[j];
nums[i] = nums[i]^nums[j];
}
}
- hash表记录某个元素是否出现,比如hash[i] = -1 表示元素i+1出现了,那么只要遍历一遍数组大等于0的就是首个未出现的正整数。
怎么维护hash表?
- 遍历一遍数组,对值小于0或者大于len+1的数值,一定不是答案,那就重新赋值为1.
- 再次遍历数组,对于数值x,取绝对值求得索引下标 i=abs(x)-1,那么对i下标的位置abs(y)数值取相反数-abs(y),这样遍历一遍,只要数组下标x位置数值为负数,就说明x+1存在。否则缺失。
剑指 Offer II 005. 单词长度的最大乘积
-
可以用一个 int 型整数记录某个字符串中出现的字符。如果字符串包含 ‘a’,那么整数最右边的数位为 1,如果字符串包含 ‘b’,那么整数从右边起倒数第 2 位为 1。这样做的好处就是能更快地判定两个字符串是否包含相同的字符。如果两个字符串包含相同的字符,那么两个整数的与运算将不等于 0。反之,如果两个字符串不包含相同的字符,那么两个整数的与运算将等于 0 。
答案
class Solution {
public int maxProduct(String[] words) {
//map去重复的字母
//特点 只需要比较字符串中的相同字母 以及相同字母数量是否相同。
//getBitMask 为什么要|而不是+,主要是mett与met拥有相同的字母,长度不同而已,但实际与其他字符串判断结果是相同。 所以|运算可以去除重复的字母。
//如果用 + : abad 1+2+1+8=12 ccc 4+4+4 12 这种实际字母组成不同但是会被直接排除在最终计算之内
//如果用 | : abad 1+2+8=11 ccc 4 对应二进制位的&也没有交集所以是正确的
HashMap<Integer,Integer> map = new HashMap<>();
for(int i=0;i<words.length;i++){
int bitmask = getBitMask(words[i]);
int l = map.getOrDefault(bitmask,0);
//如果数组中存在由相同的字母组成的不同单词,则会造成不必要的重复计算 如meet与met
map.put(bitmask,Math.max(l,words[i].length()));
}
Set<Integer> keyset = map.keySet();
int max=0;
for(int i:keyset){
for(int j:keyset){
if((i&j)==0) max = Math.max(max,map.get(i)*map.get(j));
}
}
return max;
}
int getBitMask(String str){
int bit=0;
for(int i=0;i<str.length();i++){
bit|=1<<(str.charAt(i)-'a');
}
return bit;
}
}
剑指 Offer II 007. 数组中和为 0 的三个数
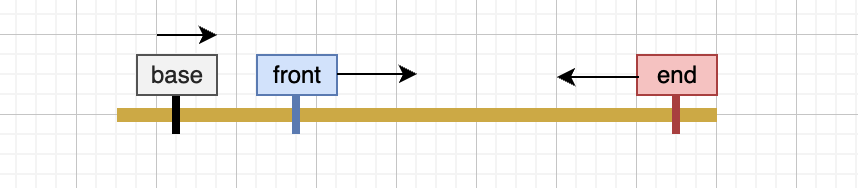
- 首先对数组排序,然后采用双指针便利
- 先左边确定一个base,然后从右边双指针遍历
- 判重
- base遍历连续相同的数值,直接跳过
- front,end指针遍历相同数值指针也直接跳过
题解
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans= new ArrayList();
Arrays.sort(nums);
int lg = nums.length;
for(int i=0;i<lg;i++){
int front = i+1;
int end = lg-1;
int total =0;
//去重
if((i>0&&nums[i]==nums[i-1])||nums[i]>0) continue;
while(front<end){
total = nums[i]+nums[front]+nums[end];
if(total<0) front++;
else if(total>0) end--;
else {
ans.add(Arrays.asList(nums[i],nums[front],nums[end]));
//去重
front++;
while(front<end&&nums[front]==nums[front-1]) front++;
while(front<end&&end+1<lg&&nums[end]==nums[end+1]) end--;
}
}
}
return ans;
}
}
数组
剑指 Offer II 008. 和大于等于 target 的最短子数组
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Rh51vKQM-1690389392989)(https://s2.loli.net/2022/02/20/pQiK7s4vb8cRonI.png)]
- 滑动窗口
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//滑动窗口
int start = 0,end = 0,sum = 0,res = Integer.MAX_VALUE;
while(end<nums.length){
sum+=nums[end];
if(sum<target) {end++;continue;}
while(start<=end&&sum>=target){
res = Math.min(res,end-start+1);
if(res==1) return 1;
sum -= nums[start++];
}
end++;
}
return res==Integer.MAX_VALUE?0:res;
}
}
剑指 Offer II 009. 乘积小于 K 的子数组

class Solution {
public int numSubarrayProductLessThanK(int[] nums, int k) {
if(k<=1) return 0;
int front=0,end=0,count=0,res=1;
while(end<nums.length){
//以右指针为基准,每次遍历一个右指针计数, 所有后缀数组
//res<k 那么久移动右指针,res累乘,res<k ,那么front~end之间的左右后缀数组都满足小于k
while(end<nums.length&&res*nums[end]<k){
res*=nums[end];
count+=(end-front+1);
end++;
}
if(end==nums.length) return count;
// 当res>k时候,1.收缩左指针(front<end) 2.两个指针都右挪(front==end)
res*=nums[end];
//System.out.println(res+","+count+"/");
while(front<end&&res>=k){
res/=nums[front++];
}
count+=(end-front+1);
end++;
}
return count;
}
}
剑指 Offer II 010. 和为 k 的子数组
-
思路前缀和:
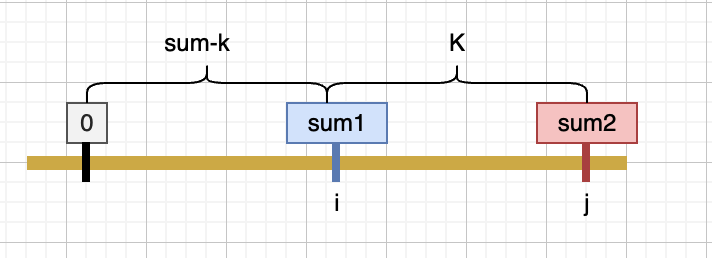
- 前缀和记录之前所有和为sum1的连续子数组之和。当遍历到sumj,假设存在以数组下标0开始以i为结尾的连输子数组之和为sum-k,那么一定存在ij的连续子数组之和为k的连续子数组,那么COUNTj~ = COUNTi。
-
map存储的是前缀和sum的个数,那么当计算到前缀和为sum的时候,从map中获取前缀和为sum-k的数量。(像动态规划。)
class Solution {
public int subarraySum(int[] nums, int k) {
//前缀和 计算前j个数字中可能的连续数组和为kk
//即为 前j的前缀和sum 前面种有多少个前缀和为sum-k的前缀数组
HashMap<Integer,Integer> map = new HashMap<>();
map.put(0,1);
int sum=0,count=0;
for(int e:nums){
sum+=e;
count+=map.getOrDefault(sum-k,0);
//前缀数组存储
map.put(sum,map.getOrDefault(sum,0)+1);
}
return count;
}
}
剑指 Offer II 011. 0 和 1 个数相同的子数组
- 前缀和+hash表
同上一个题目,将0和1个数相同的数组长度转换为和为0的最大连续子数组长度(0记为-1),map记录前缀和x的最小左下标。
references
class Solution {
public int findMaxLength(int[] nums) {
//求最长连续子数组和为0的长度
//最长连续,求和为k的连续子数组
//map存储 前缀和为sum的连续子组的下标preIndex,则当前前缀和为sum的数组下标为i。
//那么中间区间的数组和即位0 长度为i-preIndex。
//默认和为0的连续子数组下标为-1。
HashMap<Integer,Integer> map = new HashMap<>();
int sum=0,max=0;
map.put(0,-1);
for(int i=0;i<nums.length;i++){
if(nums[i]==0) sum--;
else sum++;
//存在和为sum的前缀子数组,保证一定是第一个记录的rindex
if(map.containsKey(sum)){
int preIndex = map.get(sum);
max = max>i - preIndex?max:i-preIndex;
}
//否则记录该rindex
else {
map.put(sum,i);
}
}
return max;
}
}
剑指 Offer II 013. 二维子矩阵的和
题解

- 计算二维数组的前缀和
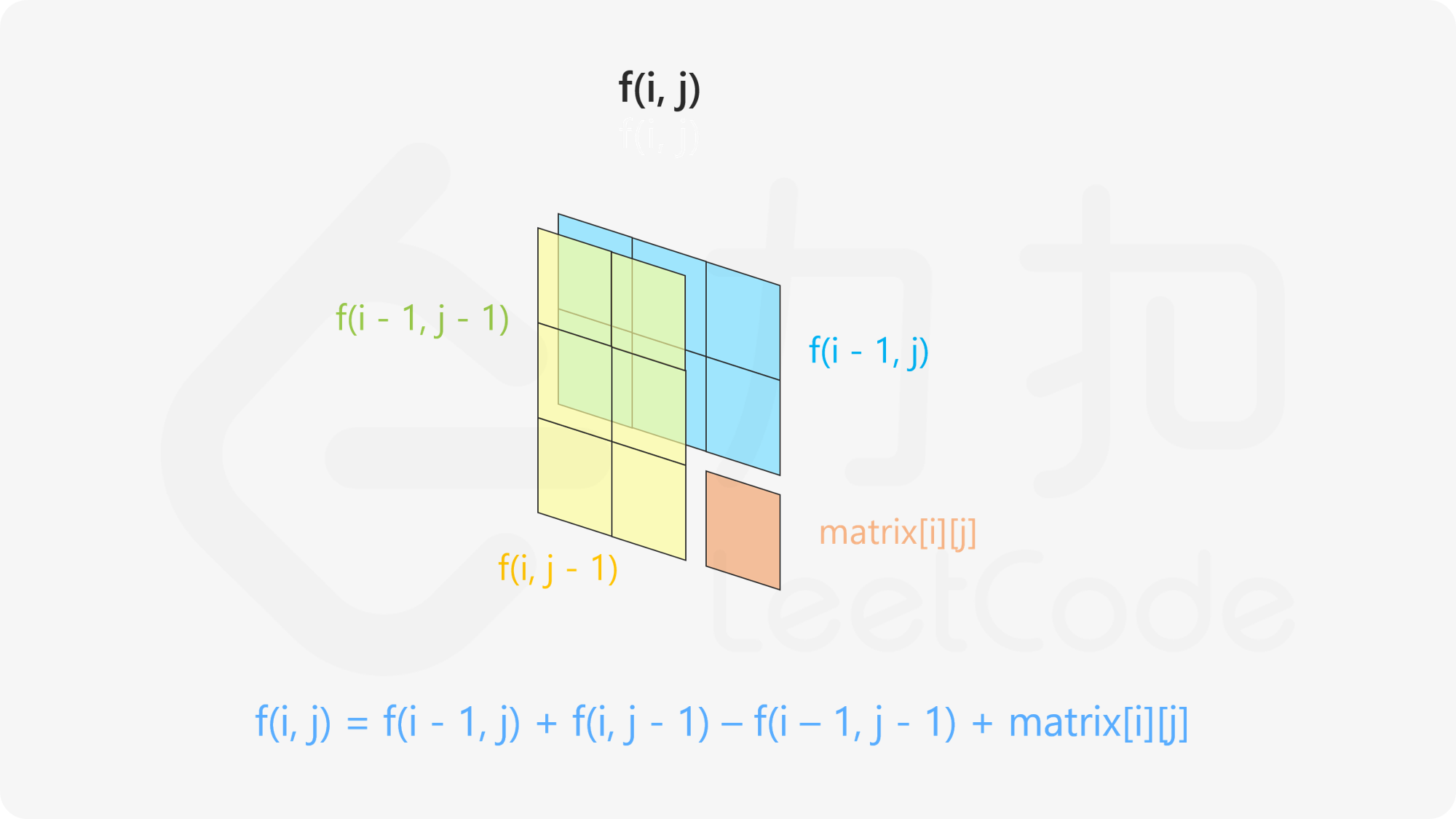
class NumMatrix {
private int [][] sum;
public NumMatrix(int[][] matrix) {
int r = matrix.length;
int l = matrix[0].length;
sum = new int[r+1][l+1];
for(int i=1;i<=r;i++){
for(int j=1;j<=l;j++){
sum[i][j] = sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];
//System.out.print(sum[i][j]+" ");
}
//System.out.println();
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sum[row2+1][col2+1] -sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];
}
}
/**
* Your NumMatrix object will be instantiated and called as such:
* NumMatrix obj = new NumMatrix(matrix);
* int param_1 = obj.sumRegion(row1,col1,row2,col2);
*/
寻找第K大
- 快排+分治
对于快排每次基于pviot对数组进行划分为大于和小于pviot的两部分,也就是说每轮分区后,pviot位置的元素位置就确定了,
- 如果pviot索引 index==K,即第K大元素,返回。
- 若果 index<K,那么第K大元素在[index+1,high]区间内
- 否则在[low,index-1]之间
时间复杂度 O(NlogK)。好坏基于pviot的选取,最欢情况O(NK)
import java.util.*;
public class Solution {
public int partion(int a[], int low, int high) {
int pviot = a[low];
while (low < high) {
while (low < high && a[high] <= pviot) {
high--;
}
if(low<high) a[low]=a[high];
while (low < high && a[low] >= pviot) {
low++;
}
if(low<high) a[high]=a[low];
}
a[low] = pviot;
return low;
}
public int quickSort(int a[],int low,int high,int K){
int t = partion(a,low,high);
if(t==K-1) return t;
if(t>K-1){
return quickSort(a,low,t-1,K);
}
else return quickSort(a,low+1,high,K);
}
public void swap(int a[], int p1, int p2) {
int t = a[p1];
a[p1] = a[p2];
a[p2] = t;
}
public int findKth(int[] a, int n, int K) {
// write code here
int t = quickSort(a,0,a.length-1,K);
return a[t];
}
}

解决方法1
随机pviot,当数组个数非常大且已是递减序列的话以及K很大的时候,时间复杂度趋于O(N2),也就是说pviot选取非常重要,使用随机数,在low,high之间最忌选取一个pviot进行分区。
import java.util.*;
public class Solution {
private Random rand = new Random();
public int partion(int a[], int low, int high) {
int index = rand.nextInt(high-low+1)+low;
int pviot = a[index];
swap(a,low,index);
while (low < high) {
while (low < high && a[high] <= pviot) {
high--;
}
if(low<high) a[low]=a[high];
while (low < high && a[low] >= pviot) {
low++;
}
if(low<high) a[high]=a[low];
}
a[low] = pviot;
return low;
}
public int quickSort(int a[],int low,int high,int K){
int t = partion(a,low,high);
if(t+1==K) return t;
if(t+1<K){
return quickSort(a,t+1,high,K);
}
else return quickSort(a,low,t-1,K);
}
public void swap(int a[], int p1, int p2) {
int t = a[p1];
a[p1] = a[p2];
a[p2] = t;
}
public int findKth(int[] a, int n, int K) {
// write code here
int t = quickSort(a,0,a.length-1,K);
return a[t];
}
}

K小堆
前面的解法都可以认为是排序算法的变种,需要对原数组进行多次访问。如果原数组特别大(上百万,甚至上亿),以至于无法存放在内存中,前面的方法就不适用了(毕竟访问外存储器的代价太大),并且pviot选取不好每次时间复杂度直接平方级别。
思路:保存K大小的小根堆,大于堆顶入。
import java.util.*;
public class Solution {
public int findKth(int[] a, int n, int K) {
// write code here
//小根堆
PriorityQueue<Integer> qu = new PriorityQueue((o1, o2)-> {
if((int)o1>(int)o2) return 1;
else return -1;
});
for (int i = 0; i < a.length; i++) {
if (qu.size() < K) {
qu.add(a[i]);
} else {
if(qu.peek()>a[i]) continue;
else{
qu.poll();
qu.add(a[i]);
}
}
}
return qu.peek();
}
}

字符串
剑指 Offer II 014. 字符串中的变位词
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-sHtKME8p-1690389392991)(https://s2.loli.net/2022/02/26/CLm2F6Qprdqyt1I.png)]
class Solution {
public boolean checkInclusion(String s1, String s2) {
//变位词判断 统计相同长度的字符串的字符串中 每个字符个数相等
int l1 = s1.length();
int l2 = s2.length();
if(l1>l2) return false;
int [] cnt1 = new int[26];
int [] cnt2 = new int [26];
int a=l1,b=-1;
for(int i=0;i<l1;i++){
int t = s1.charAt(i)-'a';
int t2 = s2.charAt(i)-'a';
cnt1[t]++;
cnt2[t2]++;
if(t<a) a = t;
if(b<t) b = t;
}
int start =0,end = l1-1;
while(end<l2){
if(compare(cnt1,cnt2,a,b)) return true;
if(end+1<l2){
int t = s2.charAt(end+1)-'a';
cnt2[t]++;
t = s2.charAt(start)-'a';
cnt2[t]--;
}
end++;
start++;
}
return false;
}
//固定字母区间 a~b
public boolean compare(int []a1,int []a2,int a,int b){
for(int i=a;i<=b;i++){
if(a1[i]!=a2[i]) return false;
}
return true;
}
}
剑指 Offer II 015. 字符串中的所有变位词
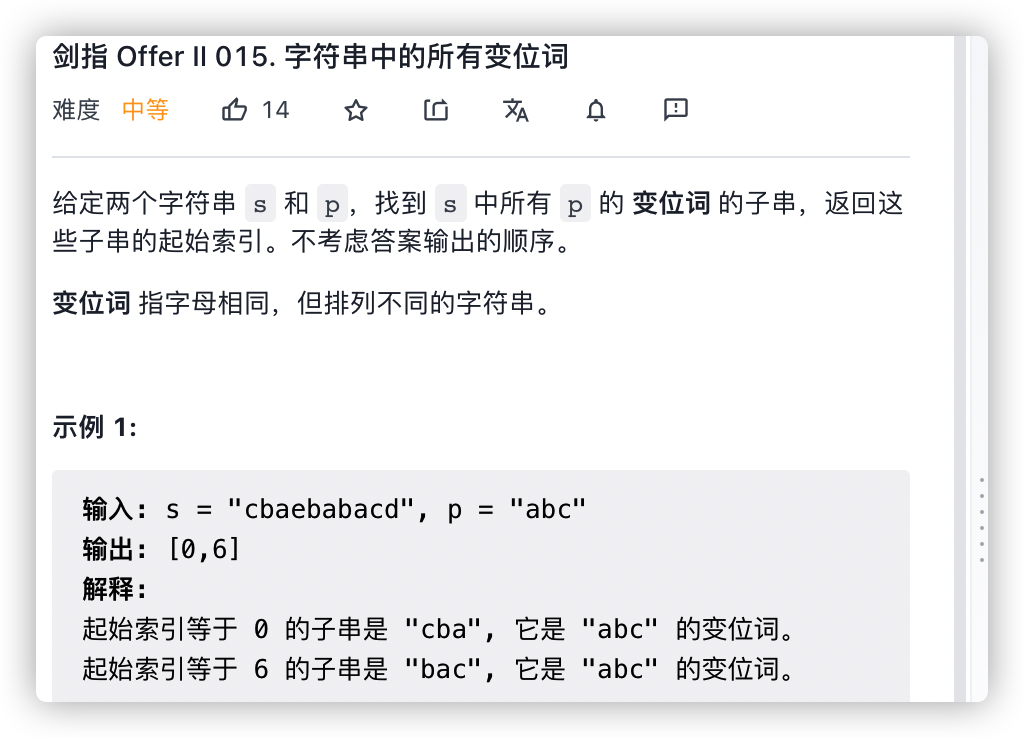
- 思路同上
class Solution {
public List<Integer> findAnagrams(String s, String p) {
int l1= s.length();
int l2 = p.length();
if(l1<l2) return new ArrayList();
List<Integer> res = new ArrayList<>();
int []cnt1 = new int[26];
int []cnt2 = new int[26];
int a=0 ,b=0;
for(int i =0;i<l2;i++)
{
int t = p.charAt(i)-'a';
cnt2[t]++;
cnt1[s.charAt(i)-'a']++;
if(t<a) a = t;
if(t>b) b =t;
}
int start=0,end =l2-1;
while(end<l1){
if(compare(cnt1,cnt2,a,b)){
res.add(start);
}
if(end+1<l1){
int t = s.charAt(end+1)-'a';
int t2 = s.charAt(start)-'a';
cnt1[t]++;
cnt1[t2]--;
}
end++;
start++;
}
return res;
}
boolean compare(int []str1,int []str2,int a,int b){
for(int i=a;i<=b;i++) {
if(str1[i]!=str2[i]) return false;
}
return true;
}
}
剑指 Offer II 016. 不含重复字符的最长子字符串
-
题解: 双指针+hashSet
- 右指针元素放入set,如果能直接放就放入,不能放入说明有相同的元素,那么就讲左指针的元素一个个从set中删除,直到set能放入右指针的元素。
class Solution {
public int lengthOfLongestSubstring(String s) {
if(s==null||s.length()==0) return 0;
if(s.length()==1) return 1;
HashSet<Character> set = new HashSet<>();
int max = 0,start=0,end=0,count=0;
while(end<s.length()){
char t = s.charAt(end);
if(!set.contains(t))
{
set.add(t);
count = end-start+1;
end++;
if(max<count) max= count;
}
else{
t = s.charAt(start);
set.remove(t);
start++;
}
}
return max;
}
}
剑指 Offer II 017. 含有所有字符的最短字符串

- 题解
- 双指针滑动窗口+hash报表
- 对s的每一个字符串计数每一个字母的数量
- 当p的每一个字母计数数组 cnt1[i] 都小于 s的计数数组cnt2[i],那么就是满足题意,否则不满足,就有指针右移,添加元素。满足就左指针右移,删除元素,继续判断是否满足题意,满足就记录最小长度。
class Solution {
public String minWindow(String s, String t) {
int ls = s.length();
int lt = t.length();
if(ls<lt) return "";
int cnt1 [] = new int[60];
int cnt2[] = new int[60];
int a=60,b=-1;
for(int i=0;i<lt;i++){
int r = t.charAt(i)-'A';
cnt2[r]++;
cnt1[s.charAt(i)-'A']++;
if(a>r) a=r;
if(b<r) b=r;
}
int left=0,right=lt-1,minLen=ls+1,rl=0,rr=0;
while(right<ls){
while(contains(cnt1,cnt2,a,b)){
if(minLen>right-left+1){
minLen = right-left+1;
rl = left;
rr = right+1;
}
int r = s.charAt(left++)-'A';
cnt1[r]--;
}
if(right+1<ls){
int r = s.charAt(right+1)-'A';
cnt1[r]++;
}
right++;
}
return s.substring(rl,rr);
}
public boolean contains(int []cnt1,int []cnt2,int a,int b){
for(int i=a;i<=b;i++){
if(cnt1[i]<cnt2[i]) return false;
}
return true;
}
}
剑指 Offer II 019. 最多删除一个字符得到回文
- 双指针,首先首尾指针遍历哪出元素不等,没有的话直接回文
- 若有不等的,那就可以左指针跳过到下一个元素,或者右指针跳过到下一个元素。这两种结果综合得解。
class Solution {
public boolean validPalindrome(String s) {
if(s==null||s.length()==0) return true;
int l = s.length();
int left=0,right=l-1;
while(left<right){
char a = s.charAt(left);
char b = s.charAt(right);
if(a!=b){
if(left+1==right) return true;
else if(left+1<right) {
return compare(s,left,right-1)||compare(s,left+1,right);
}
}
left++;
right--;
}
return true;
}
public boolean compare(String s,int l,int r){
while(l<r){
char a = s.charAt(l);
char b = s.charAt(r);
if(a!=b) return false;
l++;
r--;
}
return true;
}
}
剑指 Offer II 020. 回文子字符串的个数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aDgOPa1x-1690389392991)(https://s2.loli.net/2022/03/02/t4WUElNzd6ybwCS.png)]
- dp[j][j+i-1] 表示j~j +i-1之间的字符串为回文串(i==2的时候单独判断),那么当s[j-1]==s[j+i] 时候dp[j-1][j+i] 也是回文串。同时count计数
class Solution {
public int countSubstrings(String s) {
//dp dp[i][j] = (dp[i+1][j-1]&&i==j);
if(s==null||s.length()<=1) return s.length();
int l =s.length();
boolean [][] dp = new boolean [l][l];
int count = l;
for(int i=0;i<l;i++) dp[i][i] =true;
for(int i=2;i<=l;i++){
for(int j=0;j+i-1<l;j++){
char a = s.charAt(j);
char b = s.charAt(j+i-1);
if(i==2&&a==b){dp[j][j+i-1]=true;count++;}
else if(i>2&&a==b&&dp[j+1][j+i-2]){
dp[j][j+i-1]=true;
count++;
}
}
}
return count;
}
}
manachers算法
- 对于从回文中心开始拓展的情况分为 aba与aa。可以通过在字符串之间穿插相同的字符"#"解决,最终的字符串一定是奇数个数字母。此时只需要考虑 aba情况。
- 通过穿插"#"的字符串的, 回文字符串的长度 l = f[i]-1 (f[i]是以第i个字母为回文中心以aba方式拓展的最大回文半径(比如aba ,f[b]半径2);
- 另外字符串s : 回文个数 = (以每一个字母为回文中心的到的回文半径)L求和。此处是没有"#"穿插的字符串。 穿插后的字符串s2 : 回文个数 =以每一个字母为回文中心的到的回文半径)L/2 求和。(向下取整)。

马拉车算法的核心思想是基于以往的回文中心和(拓展)回文长度之内对称原理,减少重复的拓展,相当于动态规划。
- 题解
定义 rmax当前记录的最大回文半径右端点达到的最大下标,im当前记录的最大回文半径的回文中心下标,ans 回文个数累和。
对每一个回文中心更新回文半径:
-
针对回文中心i
- 如果 im<i<rmax, 可以定义j下标是 i关于im的对称点
j = 2*im-i。i一定大于imi关于im在左边对称的下标j,判断 j-f[j]+1是否是小于 im-f[im]+1,是那就初始化f[i] = rmax-i+1。由图可知该部分不需要重复判断,之后对i继续向右拓展得到最大的rmax。如果大于等于呢,由于对称,那就是f[j]喽。
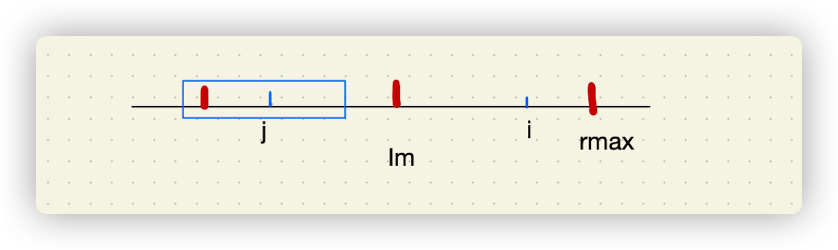
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-NgVg1QYn-1690389392992)(https://s2.loli.net/2022/03/04/EM4Do5q6SfJ8QAp.png)]
- 如果大于i>=rmax,就初始化f[i]=1。
- 然后就是对每一个f[i]暴力拓展,继续增大回文半径。
- 如果 im<i<rmax, 可以定义j下标是 i关于im的对称点
-
更新新的rmax,im
-
ans求和 ans+=f[i]/2 ,向下取整。
-
继续上面循环…
class Solution {
public int countSubstrings(String s) {
if(s==null||s.length()<=1) return s==null?0:s.length();
StringBuilder str = new StringBuilder();
str.append("?");
for(int i=0;i<s.length();i++){
str.append("#");
str.append(s.charAt(i));
}
str.append("#");
//manacher
int rmax = 0,maxlen = 0,im=0,ans = 0;
int []f = new int [str.length()];
for(int i=0;i<str.length();i++){
//i<rmax 分j+f[j]-1 超过了rm与没超过的情况。
//超过 rmax-i+1 没超过 f[j] j = 2*im-i
if(i<rmax) f[i] = Math.min(rmax-i+1,f[2*im-i]);
else f[i]=1;
//暴力拓展回文串 不管i<rmax or i>rmax。 i<rmax 且rmax-i+1没超过rmax就会自动退出拓展
for(;i-f[i]>=0&&i+f[i]<str.length()&&str.charAt(i-f[i])==str.charAt(i+f[i]);f[i]++);
//更新最大 im rmax
if(i+f[i]-1>rmax){
rmax = f[i];
im = i;
}
//回文串个数= (每一个回文中心i的回文长度)L 求和。
ans+=f[i]/2;
}
return ans;
}
}
101-分割回文字符串
- dp+深搜

class Solution {
public List<List<String>> partition(String s) {
// dp parlind[i][j] 得到字符串i~j是否为回文串,进行剪枝
boolean parlind [][]= new boolean[s.length()][s.length()];
for(int i=0;i<s.length();i++) {
parlind[i][i] = true;
if(i>0&&s.charAt(i)==s.charAt(i-1)) parlind[i-1][i] =true;
}
for(int i=3;i<=s.length();i++){
for(int j=0;j+i-1<s.length();j++){
parlind[j][j+i-1] = parlind[j][j+i-1] || parlind[j+1][j+i-2]&&s.charAt(j)==s.charAt(i+j-1);
}
}
ArrayList<List<String>> res = new ArrayList<>();
dfs(s,0,parlind,res,new ArrayList<String> ());
return res;
}
void dfs(String s,int index ,boolean parlind[][],ArrayList<List<String>> res,ArrayList<String> temp){
if(index==s.length()){
res.add(new ArrayList<String>(temp));
return ;
}
for(int i=index;i<s.length();i++){
if(parlind[index][i]){
temp.add(s.substring(index,i+1));
dfs(s,i+1,parlind,res,temp);
temp.remove(temp.size()-1);
}
}
}
}
TOPK的字符串

Map去重,堆排序。
import java.util.*;
public class Solution {
/**
* return topK string
* @param strings string字符串一维数组 strings
* @param k int整型 the k
* @return string字符串二维数组
*/
class Data {
int nums;
String value;
public Data(int n, String v) {
this.nums = n;
this.value = v;
}
}
public String[][] topKstrings (String[] strings, int k) {
// write code here
if (k <= 0||strings.length<=0) return new String[][] {};
PriorityQueue<Data> queue = new PriorityQueue<>(
(o1, o2)-> {
int n = o1.nums - o2.nums;
if (n > 0) {
return -1;
} else if (n < 0) {
return 1;
}
return o1.value.compareTo(o2.value);
}
);
HashMap<String, Integer> map = new HashMap<>();
for (int i = 0; i < strings.length; i++) {
map.put(strings[i], map.getOrDefault(strings[i], 0) + 1);
}
map.forEach((key, v)-> {
queue.add(new Data(v, key));
});
String [][] res = new String [k][2];
for (int i = 0; i < k; i++) {
Data d = queue.poll();
res[i][0] = d.value;
res[i][1] = d.nums + "";
}
return res;
}
}
链表
剑指 Offer II 022. 链表中环的入口节点
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pw1Kjpn1-1690389392993)(https://s2.loli.net/2022/03/04/RO5CIhsa6NWbpc2.png)]

/**
* Definition for singly-linked list.
* class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode detectCycle(ListNode head) {
ListNode slow=head,fast=head;
//a = c+(n-1)(b+c);
while(fast!=null){
slow = slow.next;
if(fast.next==null) return null;
fast = fast.next.next;
if(slow==fast) break;
}
if(fast==null) return null;
//注意 当fast 2倍速于slow的时候,那么当a=0,一定会在head的时候相遇。
if(fast==head) return head;
int count=0;
ListNode node=head;
while(node!=null){
count++;
node = node.next;
slow=slow.next;
if(node==slow) break;
}
return node;
}
}
剑指 Offer II 023. 两个链表的第一个重合节点
- 双指针,控制两个指针在相交点或者最终为节点相遇,控制两者走完相同的距离,假设list1长m,list长n,那么让两指针都走 m+n距离或者更少有交点的情况在第一个交点出相遇。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) {
* val = x;
* next = null;
* }
* }
*/
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//双指针,让两个指针走相同的路程 最后就会相遇
// if(headA==null||headB==null) return null;
ListNode pa = headA,pb = headB;
if(pa==null||pb==null) return null;
//最后就是一种情况 pa=pb pa为空或者不为空
while(pa!=pb){
pa = pa==null?headB:pa.next;
pb = pb==null?headA:pb.next;
}
return pa;
}
}
剑指 Offer II 025. 链表中的两数相加
- 反转链表,让最低位位头节点,然后相加。最后在反转即可。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
//反转最低位位于头节点
ListNode L1 = reverse(l1);
ListNode L2 = reverse(l2);
int count =0;ListNode head = null,node=null;
while(L1!=null||L2!=null||count>0){
int a =L1==null?0:L1.val,b = L2==null?0:L2.val;
int v = (count+a+b)%10;
count = (count+a+b)/10;
if(head==null) {head = new ListNode(v);node = head;}
else {
node.next = new ListNode(v);
node = node.next;
}
L1 =L1==null?null:L1.next;
L2 =L2==null?null:L2.next;
}
return reverse(head);
}
ListNode reverse(ListNode l){
ListNode pre = null,node = l;
while(node!=null){
ListNode temp = node.next;
node.next = pre;
pre = node;
node = temp;
}
return pre;
}
}
剑指 Offer II 026. 重排链表
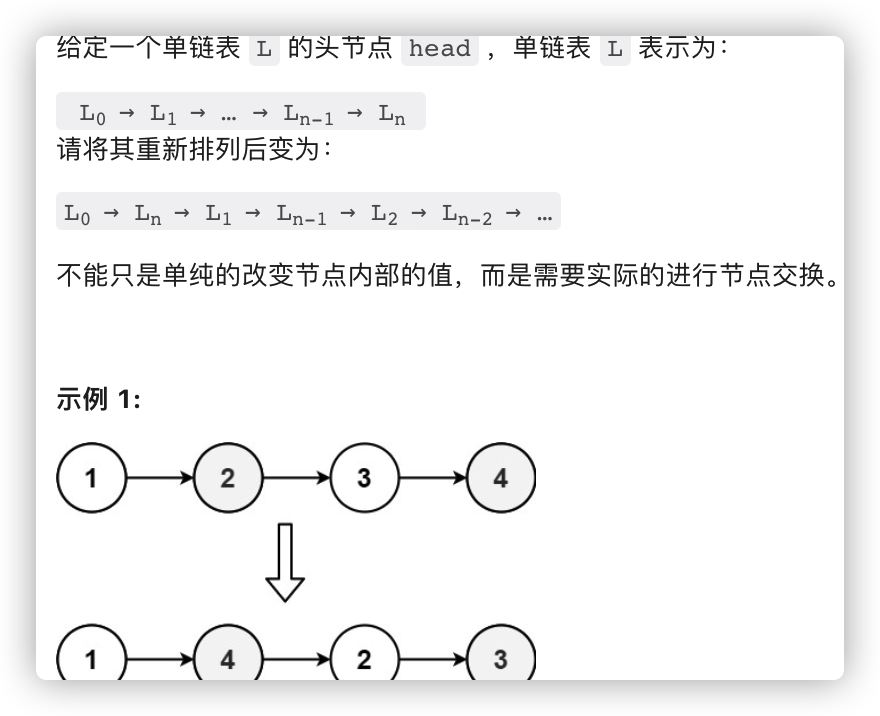
-
题解1 ,将链表存入数组,这样就可以快速访问指定位置的节点,然后再插入。
-
题解2: 时间复杂度O(n) 空间复杂度O(1)
- 找到链表的中心节点,将中心节点后的节点反转链表l2
- 然后讲两个链表的按位置间隔插入即可
快慢指针快速找到链表中心节点fast2,slow1。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public void reorderList(ListNode head) {
//寻找中间节点 fast slow指针
ListNode mid = middle(head);
//反转右半边
ListNode right = reverse(mid),left = head;
//合并 right可能比left长
ListNode rNext = null,lNext = null;
while(left!=null){
rNext = right.next;
lNext =left.next;
left.next = right;
right.next=lNext;//可能提前为 lNext = null
right=rNext;
left = lNext;
}
}
ListNode reverse(ListNode l){
ListNode pre = null,node = l;
while(node!=null){
ListNode temp = node.next;
node.next = pre;
pre = node;
node = temp;
}
return pre;
}
ListNode middle(ListNode head){
ListNode fast = head,slow = head;
while(fast.next!=null&&fast.next.next!=null){
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
// void print()
}
剑指 Offer II 027. 回文链表
- 题解同上,其中对于反转后得到的两个链表,如果一个链表多出一个元素,直接跳过不需要判断。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode mid = middle(head);
ListNode l2 = reverse(mid);
while(l2!=null&&head!=null){
if(head.val!=l2.val) return false;
head = head.next;
l2=l2.next;
}
return true;
}
ListNode middle(ListNode head){
ListNode fast = head,slow = head;
while(fast.next!=null&&fast.next.next!=null){
fast=fast.next.next;
slow = slow.next;
}
return slow;
}
ListNode reverse(ListNode l){
ListNode pre=null,node = l;
while(node!=null)