题意

给你一段区间[x, y]求其中满足一个数恰好等于K个互不相等的B的整数次幂之和的数的个数。
例如：x = 15, y = 20, k = 2, b = 2，那么对于这个区间有且仅有三个数满足题意：
$17=2^4+2^0=10001$
$18=2^4+2^1=10010$
$20=2^4+2^2=10100$

思路

对于这种题型一眼就看出是数位DP了。那么对于数位DP的技巧我在上一篇博客提到过链接: 数位DP技巧但是对于上一篇博客只是对于技巧1和分类讨论作了明确的说明，但是对于技巧2结合树形结构并没有细说。那么对于本题我们采用技巧2对于我们解决很有帮助。首先得知技巧1我们能够通过前缀和的方式。来求出问题提到符合区间的个数也就是f[y]-f[x-1]。那么我们如何求出区间[1,N]的符合条件的个数呢。

首先我们先分析一下本题。什么数才是满足条件的，其实就是将一个数转化成b进制，这个数有且仅有k个1出现就是符合条件的数。
那么现在我们将N转化成b进制得到n位数分别是$a_{n-1},a_{n-2},...,a_0$

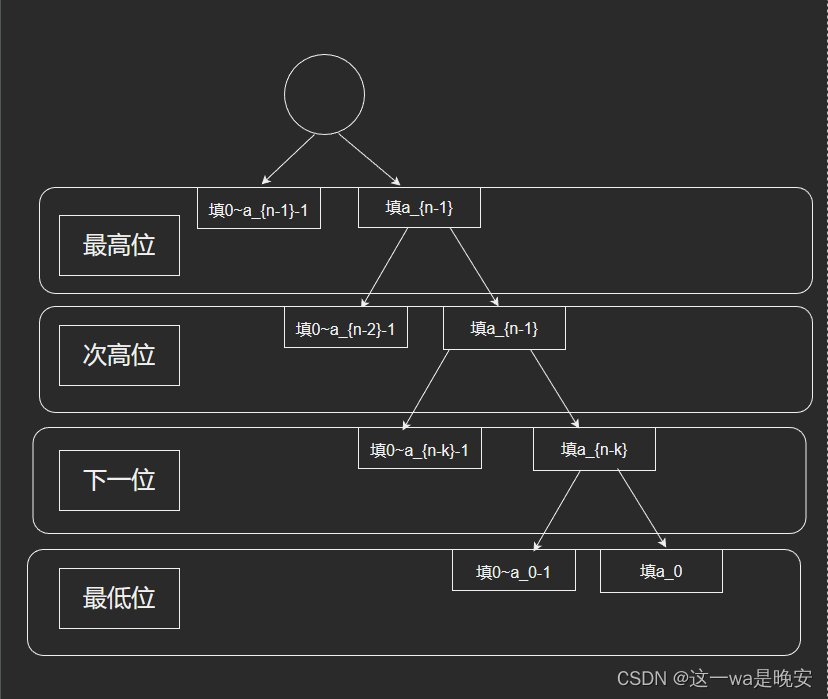
那么我们按照以上的分法我们可以看出对于每一位的右侧我们是固定的。那么对于左侧的情况我们是不确定的。如果我们能够直接算出每一位左边的情况而不是枚举的话显然这样大大的节约了时间。实际上绝大多数的数位DP问题就是像上述一样将这个区间的最大值分成n位数。然后按照上述的分法去分类讨论每一位的情况。那么对于左边的算法的话一般就是利用动态规划或者排列组合去计算。对于本题来说我们是要看这n位b进制数有多少种选法使得有k个1。那么以最高位举例来说。对于右边来说我们没多大讨论的。如果是左侧选1的话那么对于后面的n-1位就要选出k-1个1出来也就是有$c_{n-1}^{k-1}$种情况。如果左侧不选一的话对于后面n-1位来说就要选出k个1也就是有$c_{n-1}^k$种情况了。所以对于最高位如果$a_{n-1}$大于1那么一共就会有$c_{n-1}^{k-1}+c_{n-1}^k$贡献。为什么是大于1代码里面会细说。

代码

#include<bits/stdc++.h>

using namespace std;

const int N = 35;

int c[N][N];

int l, r, k, b;

void init() //递归求组合数
{
    for(int i = 0; i < N; i ++)
    {
        for(int j = 0; j <= i; j ++)
        {
            if(!j) c[i][j] = 1;
            else
                c[i][j] = c[i-1][j] + c[i-1][j-1];
        }
    }
}

int dp(int n)
{
    if(!n) return 0;

    vector<int> num;

    while(n)
    {
        num.push_back(n%b);
        n /= b;
    }//拆分成n位b进制数

    n = num.size();
    int res = 0; //统计答案
    int last = 0; //统计前面右边已经用多少个1

    for(int i = n-1; i >= 0; i --)
    {
        int x = num[i];
        // 求左边的情况，为什么这里不枚举[0~a_{n-1}]，因为由题意知道我们是要看n位b进制数是否有k个1，我们这儿每一位只会取0和1。
        // 如果这一位为0，那么就进不去左边了。如果不为0那么我们才能进去。
        if(x)
        {
            res += c[i][k-last]; //左边不为1
            if(x > 1) //因为左边是0~x-1,如果x不大于1那么我左边就不能选1，所以我左边能选1的情况一定是x要大于1才行。
            {
                if(k - last -1 >= 0)res += c[i][k-last-1]; //因为只能取k个1,还要减去前面右边用了多少个1
                break;
            }
            else // x = 1,只能右边为1
            {
                last++;
                if(last > k) break;
            }
        }
        if(!i && last == k) res++; //统计右边的情况。
    }
    return res;
}

signed main()
{
    init();
    cin >> l >> r >> k >> b;
    cout << dp(r) - dp(l-1) << endl; //技巧1前缀和思想
    return 0;
}