递归

生活中的故事

递归的概念

递归的必要条件

示例

递归执行过程分析

代码示例

递归练习

练习一

执行过程图

练习二

执行过程图

练习三

执行流程图

编辑斐波那契数列

汉诺塔

汉诺塔问题解析

总结

递归

关于递归博主在C语言部分也进行了详解，java中递归与其类似，感兴趣的可以点下方链接进行了解

递归函数实例讲解_递归实例讲解_遇事问春风乄的博客-CSDN博客https://blog.csdn.net/m0_71731682/article/details/130534063?spm=1001.2014.3001.5501 青蛙跳台阶问题的简单实现与理解（递归实现）_遇事问春风乄的博客-CSDN博客https://blog.csdn.net/m0_71731682/article/details/130482735?spm=1001.2014.3001.5501 C语言初识函数二_遇事问春风乄的博客-CSDN博客https://blog.csdn.net/m0_71731682/article/details/130504398?spm=1001.2014.3001.5501

生活中的故事

我们先来看一个故事

从前有坐山，山上有座庙，庙里有个老和尚给小和尚将故事，讲的就是：
"从前有座山，山上有座庙，庙里有个老和尚给小和尚讲故事，讲的就是：
"从前有座山，山上有座庙..."
"从前有座山……"

上面的故事的特征：自身中又包含了自己，该种思想在数学和编程中非常有用，因为有些时候，我们遇到的问题直接并不好解决，但是发现将原问题拆分成其子问题之后，子问题与原问题有相同的解法，等子问题解决之后，原问题就迎刃而解了

递归的概念

一个方法在执行过程中调用自身, 就称为 "递归".
递归相当于数学上的 "数学归纳法", 有一个起始条件, 然后有一个递推公式.

例如, 我们求 N!
起始条件: N = 1 的时候, N! 为 1. 这个起始条件相当于递归的结束条件.
递归公式: 求 N! , 直接不好求, 可以把问题转换成 N! => N * (N-1)!

递归的必要条件

1. 将原问题划分成其子问题，注意：子问题必须要与原问题的解法相同
2. 递归出口

示例

递归求 N 的阶乘

public static void main(String[] args) {
        int n = 5;
        int ret = factor(n);
        System.out.println("ret = " + ret);
    }
    public static int factor(int n) {
        if (n == 1) {
            return 1;
        }
        return n * factor(n - 1); // factor 调用函数自身
    }

递归执行过程分析

递归的程序的执行过程不太容易理解, 要想理解清楚递归, 必须先理解清楚 "方法的执行过程", 尤其是 "方法执行结束之后, 回到调用位置继续往下执行"

代码示例

public class Main {
    public static void main(String[] args) {
        int n = 5;
        int ret = factor(n);
        System.out.println("ret = " + ret);
    }
    public static int factor(int n) {
        System.out.println("函数开始, n = " + n);
        if (n == 1) {
            System.out.println("函数结束, n = 1 ret = 1");
            return 1;
        }
        int ret = n * factor(n - 1);
        System.out.println("函数结束, n = " + n + " ret = " + ret);
        return ret;
    }
}

结果展示

执行过程图

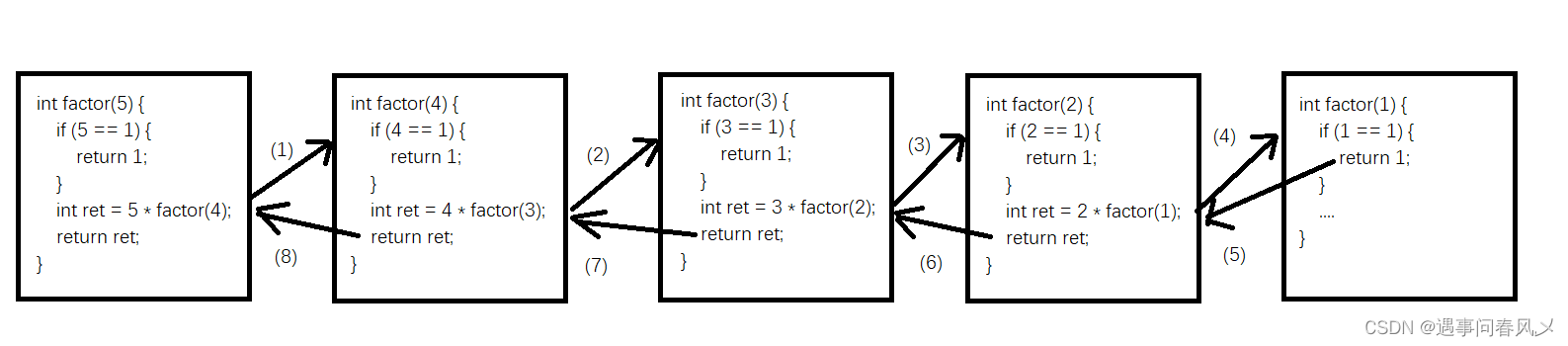
程序按照序号中标识的 (1) -> (8) 的顺序执行，

其中（1）--（4）为递的过程

（5）--（8）为归的过程

递归练习

练习一

按顺序打印一个数字的每一位

(例如 1234 打印出 1 2 3 4)

public static void print(int num) {
    if (num > 9) {
        print(num / 10);
    } 
    System.out.println(num % 10);
}

执行过程图

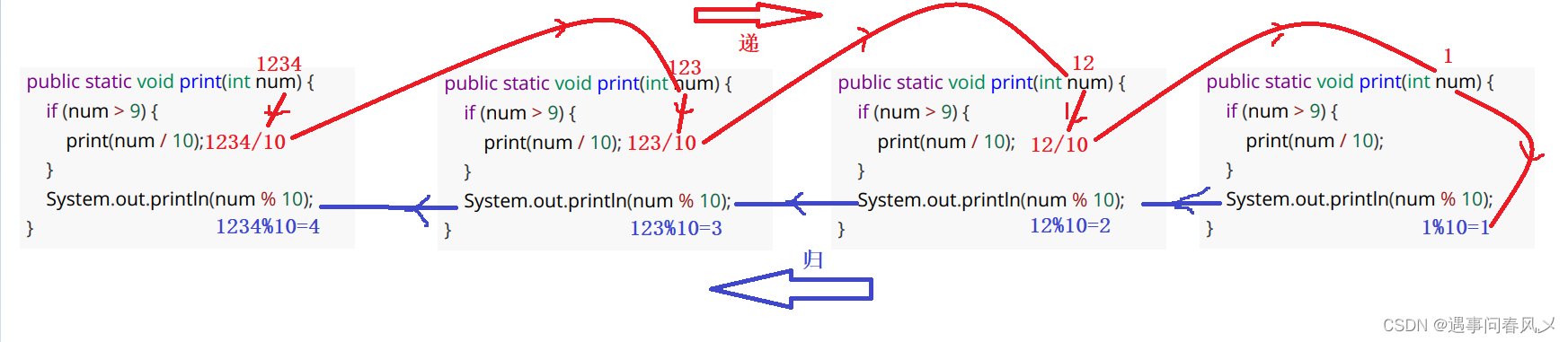
练习二

递归求 1 + 2 + 3 + ... + 10

public static int sum(int num) {
    if (num == 1) {
        return 1;
    } 
    return num + sum(num - 1);
}

执行过程图

练习三

写一个递归方法，输入一个非负整数，返回组成它的数字之和. 例如，输入 1729, 则应该返回
1+7+2+9，它的和是19

public static int sum(int num) {
    if (num < 10) {
        return num;
}
    return num % 10 + sum(num / 10);
}

执行流程图

斐波那契数列

斐波那契数列介绍:

斐波那契数列 - 搜狗百科 (sogou.com)https://baike.sogou.com/v267267.htm?fromTitle=%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0%E5%88%97

代码实现如下

public static int fib(int n) {
    if (n == 1 || n == 2) {
        return 1;
    } 
    return fib(n - 1) + fib(n - 2);
}

当我们求 fib(40) 的时候发现, 程序执行速度极慢. 原因是进行了大量的重复运算

  class Test {
        public static int count = 0; // 这个是类的成员变量. 后面会详细介绍到
        public static void main(String[] args) {
            System.out.println(fib(40));
            System.out.println(count);
        }
        public static int fib(int n) {
            if (n == 1 || n == 2) {
                return 1;
            } if
            (n == 3) {
                count++;
            } 
            return fib(n - 1) + fib(n - 2);
        }
    }


// 执行结果
102334155
39088169 // fib(3) 重复执行了 3 千万次

可以使用循环的方式来求斐波那契数列问题, 避免出现冗余运算

 public static int fib(int n) {
        int last2 = 1;
        int last1 = 1;
        int cur = 0;
        for (int i = 3; i <= n; i++) {
            cur = last1 + last2;
            last2 = last1;
            last1 = cur;
        } 
        return cur;
    }

此时程序的执行效率大大提高了
这也是递归存在的弊端

汉诺塔

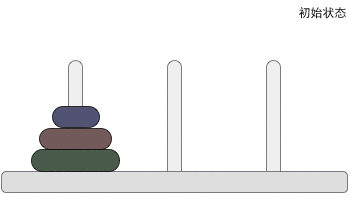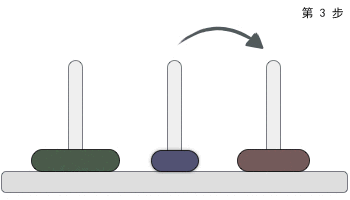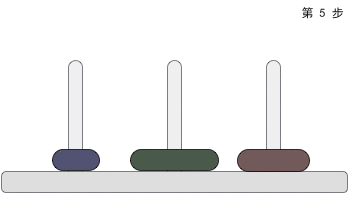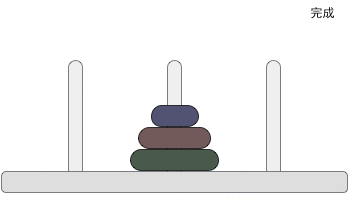
汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

汉诺塔问题解析

为了方便讲解，我们将 3 个柱子分别命名为起始柱、目标柱和辅助柱。实际上，解决汉诺塔问题是有规律可循的：
1) 当起始柱上只有 1 个圆盘时，我们可以很轻易地将它移动到目标柱上；

2) 当起始柱上有 2 个圆盘时，移动过程如下图所示

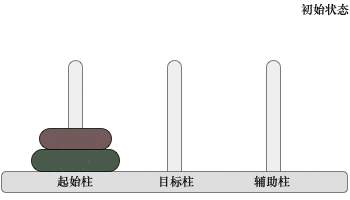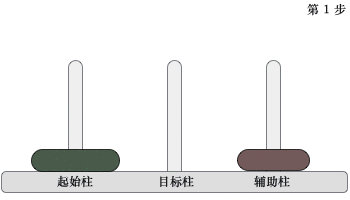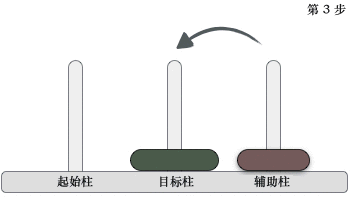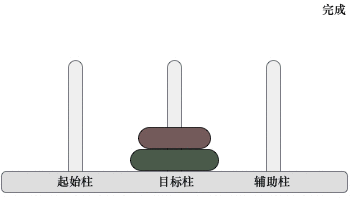
移动过程是：先将起始柱上的 1 个圆盘移动到辅助柱上，然后将起始柱上遗留的圆盘移动到目标柱上，最后将辅助柱上的圆盘移动到目标柱上。

3) 当起始柱上有 3 个圆盘时，移动过程如图 2 所示，仔细观察会发现，移动过程和 2 个圆盘的情况类似：先将起始柱上的 2 个圆盘移动到辅助柱上，然后将起始柱上遗留的圆盘移动到目标柱上，最后将辅助柱上的圆盘移动到目标柱上。

通过分析以上 3 种情况的移动思路，可以总结出一个规律：对于 n 个圆盘的汉诺塔问题，移动圆盘的过程是：

将起始柱上的 n-1 个圆盘移动到辅助柱上；
将起始柱上遗留的 1 个圆盘移动到目标柱上；
将辅助柱上的所有圆盘移动到目标柱上。

由此，n 个圆盘的汉诺塔问题就简化成了 n-1 个圆盘的汉诺塔问题。按照同样的思路，n-1 个圆盘的汉诺塔问题还可以继续简化，直至简化为移动 3 个甚至更少圆盘的汉诺塔问题。

汉诺塔问题的伪代码如下：

// num 表示移动圆盘的数量，source、target、auxiliary 分别表示起始柱、目标柱和辅助柱
hanoi(num , source , target , auxiliary): 
    if num == 1:     // 如果圆盘数量仅有 1 个，则直接从起始柱移动到目标柱
        print(从 source 移动到 target)
    else:
        // 递归调用 hanoi 函数，将 num-1 个圆盘从起始柱移动到辅助柱上，整个过程的实现可以借助目标柱
        hanoi(num-1 , source , auxiliary , target)
        // 将起始柱上剩余的最后一个大圆盘移动到目标柱上
        print(从 source 移动到 target) 
        // 递归调用 hanoi 函数，将辅助柱上的 num-1 圆盘移动到目标柱上，整个过程的实现可以借助起始柱               
        hanoi(n-1 , auxiliary , target , source)

代码实现

        // 统计移动次数
        public static int i = 1;
        public static void hanoi(int num, char sou, char tar, char sux) {
            // 如果圆盘数量仅有 1 个，则直接从起始柱移动到目标柱
            if (num == 1) {
                System.out.println("第" + i + "次:从" + sou + "移动到" + tar);
                i++;
            } else {
                // 递归调用 hanoi() 函数，将 num-1 个圆盘从起始柱移动到辅助柱上
                hanoi(num - 1, sou, sux, tar);
                // 将起始柱上剩余的最后一个大圆盘移动到目标柱上
                System.out.println("第" + i + "次:从" + sou + "移动到" + tar);
                i++;
                // 递归调用 hanoi() 函数，将辅助柱上的 num-1 圆盘移动到目标柱上
                hanoi(num - 1, sux, tar, sou);
            }
        }
        public static void main(String[] args) {
            // 以移动 3 个圆盘为例，起始柱、目标柱、辅助柱分别用 A、B、C 表示
            hanoi(3, 'A', 'B', 'C');
        }

运行结果如下