56、完全平方数

(1) 题目解析

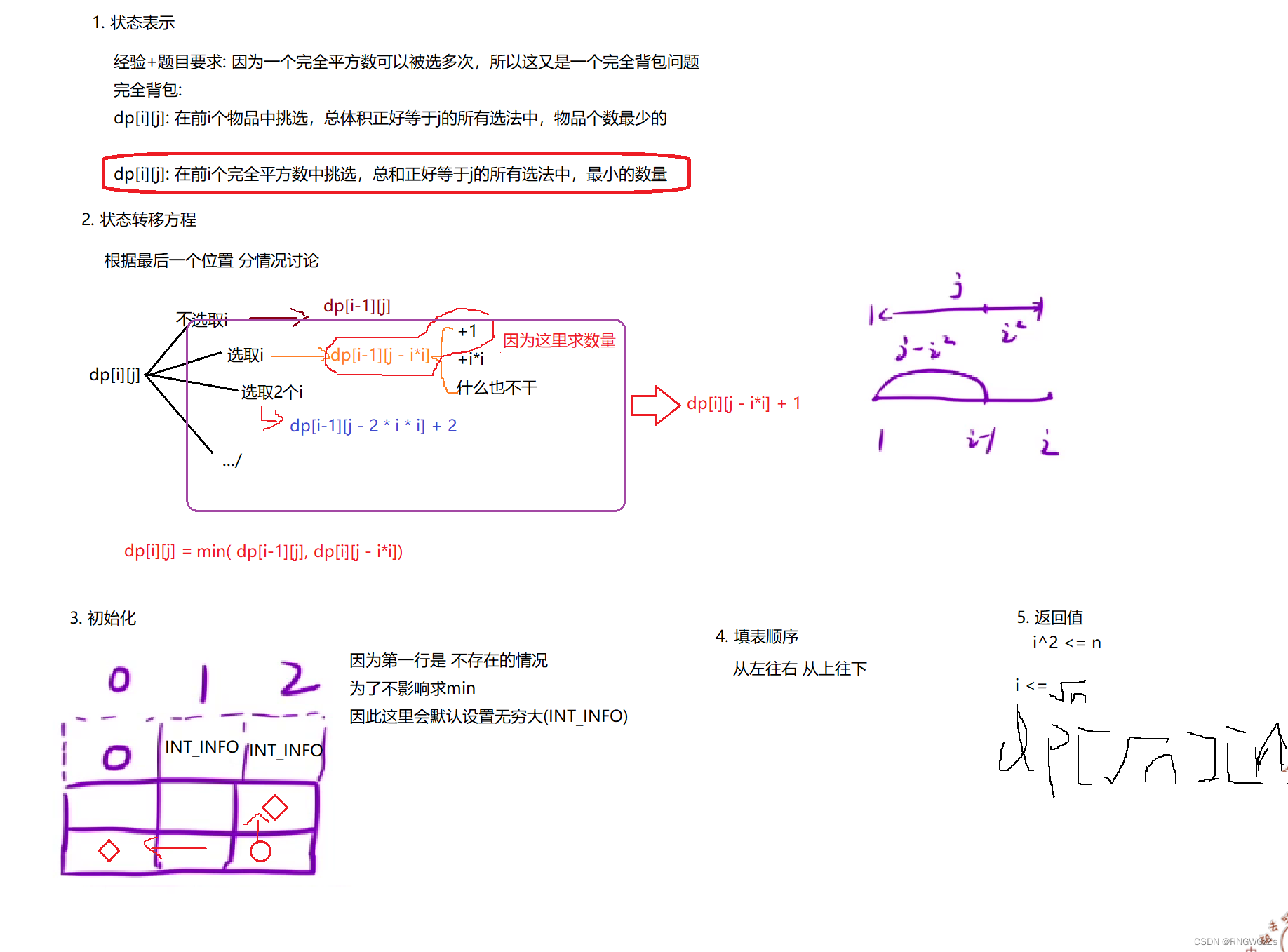
把题目解释到了这个份上，你很难不把思路转移到考虑 "背包问题上"。

(2) 算法原理

class Solution {
public:
    int numSquares(int n) {
        int m = sqrt(n);
        vector<vector<int>> dp(m+1,vector<int>(n+1));
        const int INT_INFO = 0x3f3f3f3f;
        // 初始化
        dp[0][0] = 0;
        for(int j=1;j<=n;++j) dp[0][j] = INT_INFO;

        for(int i=1;i<=m;++i)
            for(int j=0;j<=n;++j)
            {
                dp[i][j] = dp[i-1][j];
                if(j >= i*i) dp[i][j] = min(dp[i][j],dp[i][j - i*i]+1);
            }
        return dp[m][n];
    }
};

优化:

class Solution {
public:
    int numSquares(int n) {
        int m = sqrt(n);
        vector<int> dp(n+1);
        const int INT_INFO = 0x3f3f3f3f;
        // 初始化
        dp[0] = 0;
        for(int j=1;j<=n;++j) dp[j] = INT_INFO;

        for(int i=1;i<=m;++i)
            for(int j=i*i;j<=n;++j) // 完全背包 从左往右
            {
                dp[j] = min(dp[j],dp[j - i*i]+1);
            }
        return dp[n];
    }
};

57、一和零

(1) 题目解析

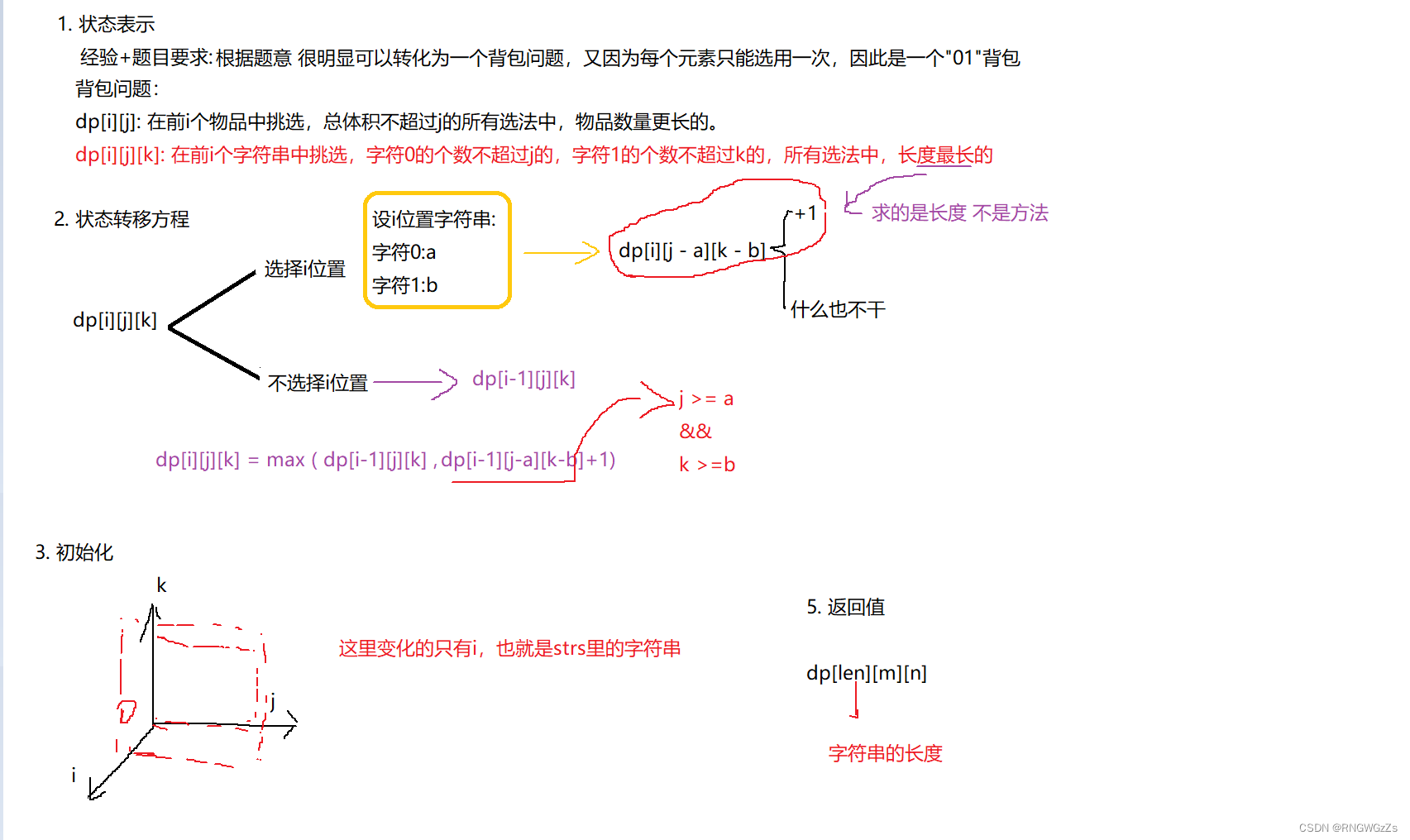
唯一的不同在于，之前做的"背包问题"的条件大抵是一个，而现在的场景时两个。由此，这类问题又被称为 " 二维费用背包问题 "。

(2) 算法原理

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len = strs.size();
        // 三维dp
        vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(m+1,vector<int>(n+1)));

        for(int i=1;i<=len;++i)
        {
            // 统计字符
            int a = 0,b=0;
            for(auto& e:strs[i-1])
            {
                if(e == '0') a++;
                else b++;
            }

            for(int j=0;j<=m;++j)
            {
                for(int k=0;k<=n;++k)
                {
                    dp[i][j][k] = dp[i-1][j][k];
                    if(j>=a && k>=b) dp[i][j][k] = max( dp[i][j][k], dp[i-1][j-a][k-b] + 1);
                }
            }
        }

        return dp[len][m][n];
    }
};

优化:

class Solution {
public:
    int findMaxForm(vector<string>& strs, int m, int n) {
        int len = strs.size();
        // 二维dp
        vector<vector<int>> dp(m+1,vector<int>(n+1));

        for(int i=1;i<=len;++i)
        {
            // 统计字符
            int a = 0,b=0;
            for(auto& e:strs[i-1])
            {
                if(e == '0') a++;
                else b++;
            }
            // 01背包 从右往左
            for(int j=m;j>=a;--j)
            {
                for(int k=n;k>=b;--k)
                {
                    dp[j][k] = max(dp[j][k], dp[j-a][k-b] + 1);
                }
            }
        }
        return dp[m][n];
    }
};

58、盈利计划

(1) 题目解析

(2) 算法原理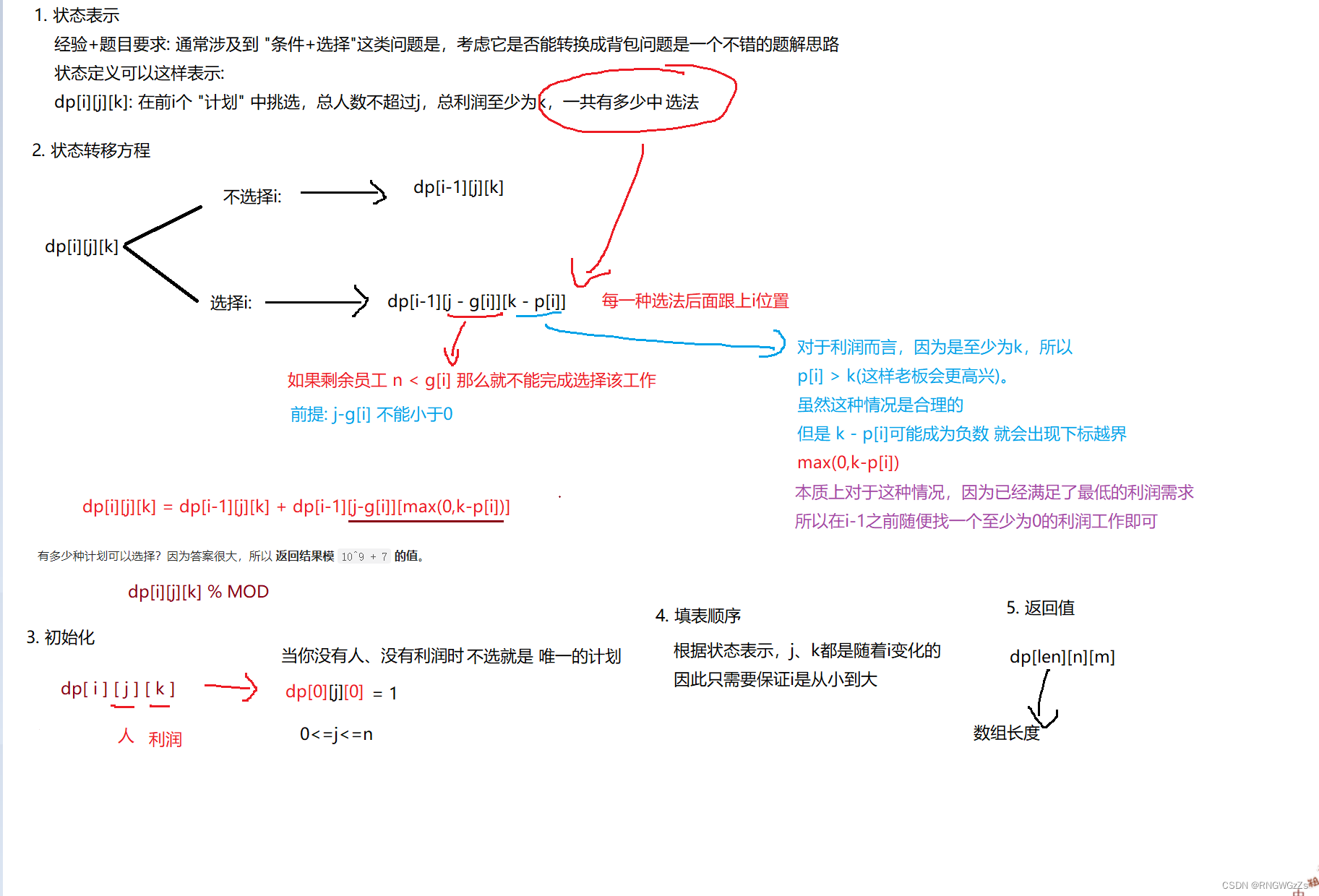

class Solution {
public:
    int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p) {
         int len = g.size();
         vector<vector<vector<int>>> dp(len+1,vector<vector<int>>(n+1,vector<int>(m+1)));
         // 初始化 人数
         for(int j=0;j<=n;++j) dp[0][j][0] = 1;
         const int MOD = 1e9+7;
         for(int i=1;i<=len;++i)
            for(int j=0;j<=n;++j)
                for(int k=0;k<=m;++k)
                {
                    dp[i][j][k] = dp[i-1][j][k];
                    if(j>=g[i-1]) dp[i][j][k] += dp[i-1][j-g[i-1]][max(0,k-p[i-1])];
                    dp[i][j][k] %= MOD;
                }

        return dp[len][n][m];
    }
};

优化:

class Solution {
public:
    int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p) {
         int len = g.size();
         vector<vector<int>> dp(n+1,vector<int>(m+1));
         // 初始化 人数
         for(int j=0;j<=n;++j) dp[j][0] = 1;
         const int MOD = 1e9+7;

         for(int i=1;i<=len;++i)
            for(int j=n;j>=g[i-1];--j) // 01背包从右往左
                for(int k=m;k>=0;--k) // k没有什么限制条件>=0即可
                {
                    dp[j][k] += dp[j-g[i-1]][max(0,k-p[i-1])];
                    dp[j][k] %= MOD;
                }

        return dp[n][m];
    }
};

59、组合总和Ⅳ

(1) 题目解析

有了上面好几道题的铺垫，emm我们来看看这道题，从nums选数，这不就是类似选物品吗？再让选取的数最后等于target，这不就类似最后将背包装满嘛？可是真的是这样吗？

所以，本题是一道看似背包，但其实跟背包问题打不着杆的题型。

(2) 算法原理

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        int n = nums.size();

        vector<double> dp(target+1,0);
        dp[0] = 1;
        // 凑成i的数
        for(int i=1;i<=target;++i)
            // 枚举nums
            for(auto& e:nums)
            {
                // i >= nums[j]
                if(i >= e){
                    dp[i] += dp[i - e];
                }
            }
        return dp[target];
    }
};

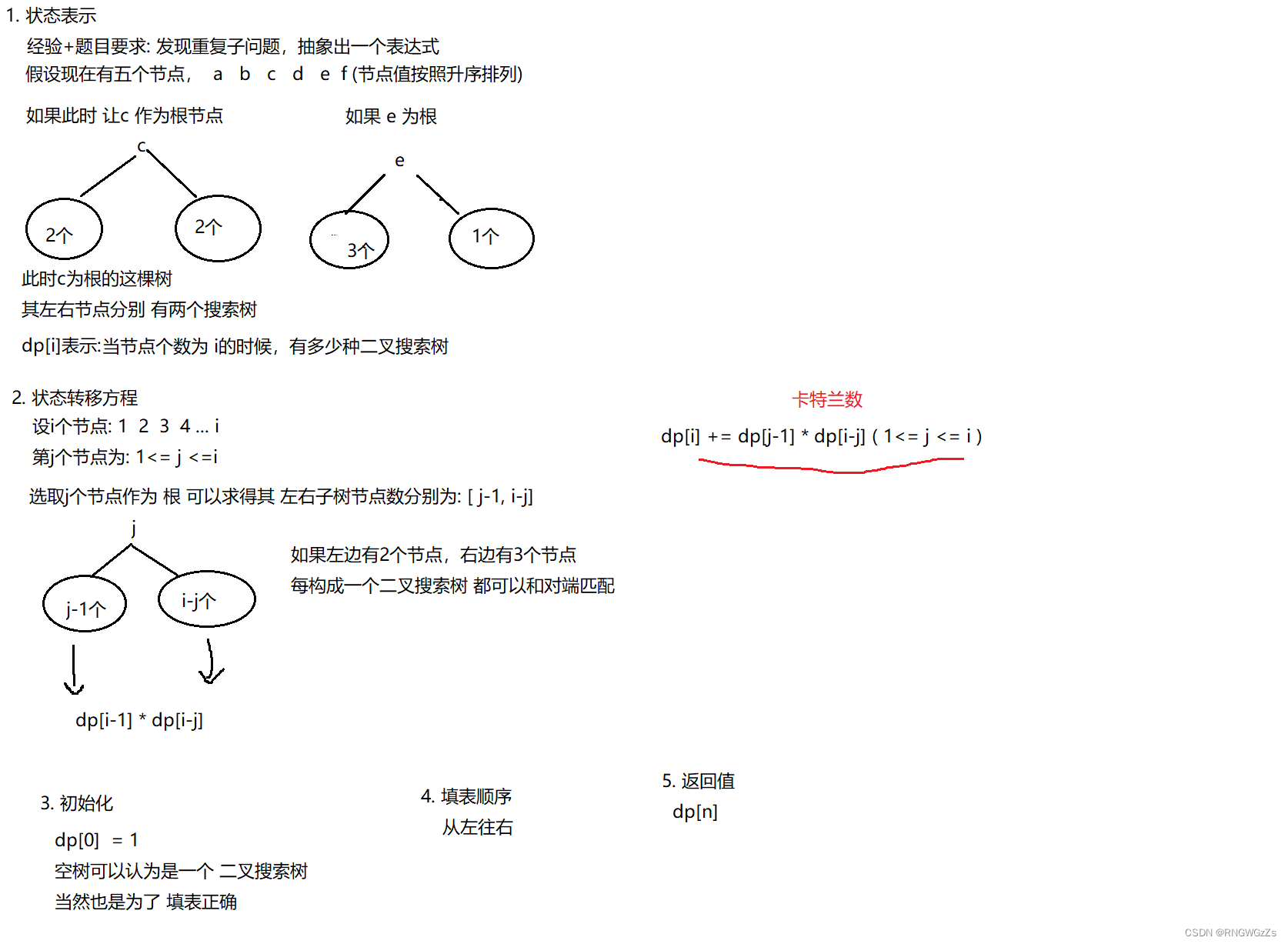
60、不同的二叉搜索树

(1) 题目解析

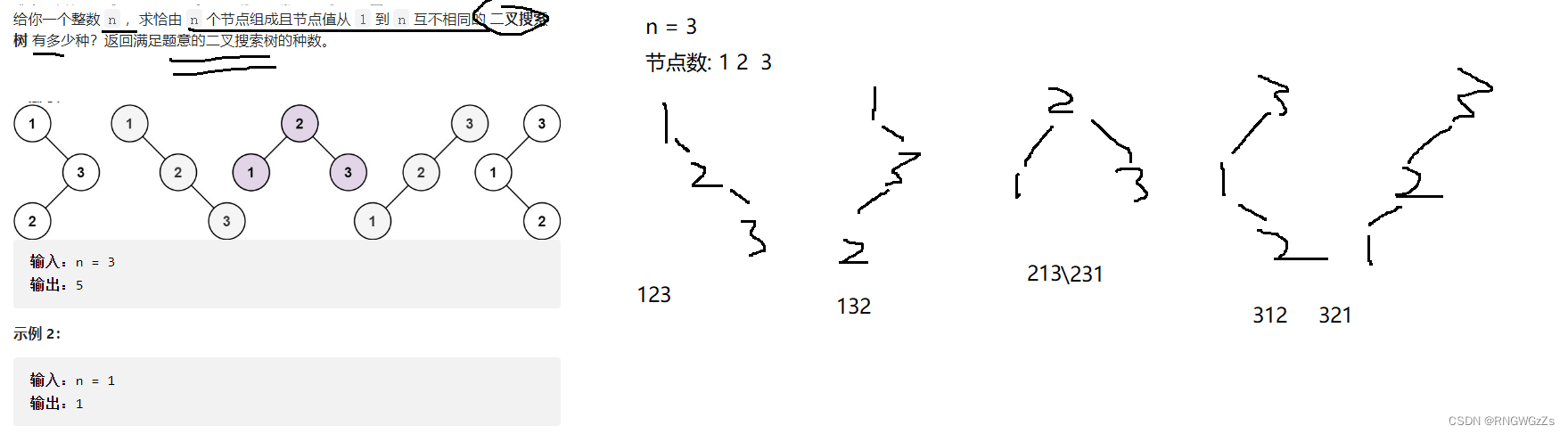
唔，节点数为n，生成的节点值是1~n，要求的是节点值构成节点数n的种树有多少。这似乎很“背包问题”。因为又是一种选数(节点)，最后构成容量(节点数)为n的过程。但，题解也能看出来，不是简单的选节点。

(2) 算法原理

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1);
        dp[0] = 1;

        for(int i=1;i<=n;++i)
            for(int j=1;j<=i;++j) // 枚举 0~i
                dp[i] += dp[j-1] * dp[i-j];
        
        return dp[n];
    } 
};

那么本栏的dp问题也就到此结束，祝愿诸位能在算法上找到自己的解题思路和技巧。

本篇到此结束，感谢你的阅读。

祝你好运，向阳而生~