概述

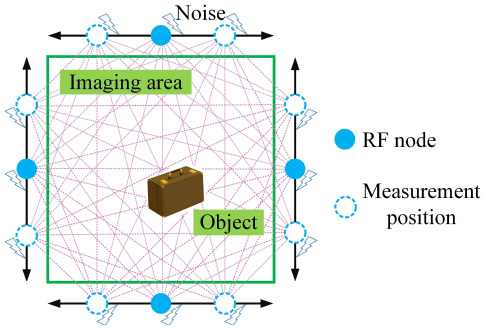
无线电层析成像是一种通过获取一定区域内多对相对固定的无线通信节点间的某种测量数据后,按照一定的数学处理方法,对区域内的障碍物目标以图像的形式
展现出来的成像技术。

开山之作：
J. Wilson and N. Patwari, “Radio tomographic imaging with wireless networks,”
IEEE Trans. Mobile Comput., vol. 9, no. 5, pp. 621–632,May 2010.
Radio tomographic imaging with wireless networks

优势：

不要求物体佩戴任何设备；
无线电波可以穿透物理结构。

初始化环境参数

代码是初始化环境参数，并生成用于深度学习的训练数据和测试数据的代码。主要包括以下部分：

输入参数：包括移动射频节点数量、每个节点收集数据的航点数、信噪比范围、路径损耗指数范围、全球平均发射功率水平范围、信号角度范围、Kappa参数（用于生成空间相关的高斯随机场）、节点遍历区域大小、图像原点坐标、图像大小、像素大小、白色像素的衰减、垂直、水平和方形墙的最小/最大值等。

数据预分配：预先分配一些变量的空间，包括像素数、UWB链路数、每个链路的UWB数据数等。

节点位置计算：根据输入参数计算每个节点的所有坐标。

数据存储：预先分配存储数据的空间，包括节点位置、UWB节点间距离、SLF权重、不匹配实验的SLF权重和偏置的权重。

生成权重和距离：根据节点位置和输入参数生成SLF权重和UWB节点间距离。

生成空间相关的高斯随机场：根据图像大小、像素大小和Kappa参数生成空间相关的高斯随机场，并进行Cholesky分解得到上三角矩阵。

%M：移动RF节点的数量
%Tw：每个节点收集数据的航点数
%sig_epsilon_range：噪声信噪比的范围
%alpha_range：路径损耗指数的范围
%b_range：全局平均发射功率水平的范围
%sig_theta_range：SLF图像的标准差范围
%kappa：空间相关性高斯随机场的参数
%areabounds：节点遍历区域的大小
%imgorg：图像的左下角坐标
%imgdims：图像的大小（像素）
%pixelsize：每个像素的长度/宽度 %dBwhite：白色像素的衰减值（分贝）
%wallcount_vec：垂直、水平和方形墙壁的最小/最大数量

clear; clc; close all;  % 清空命令窗口、清空工作区、关闭所有图窗

M  = 4;              %number of mobile RF nodes  移动射频节点的数量
Tw = 6;              %number of waypoints for each node to gather data from  每个节点收集数据的航点数，一条边上有6个航点
sig_epsilon_range = [0.3,1,3];    % SNR is about 30,40,50  信噪比约为30、40、50
%对于信噪比（SNR），通常使用以分贝（dB）为单位的对数比值来表示。在这里，sig_epsilon_range = [0.3,1,3] 是指信噪比的范围，其中的值是对应于SNR的对数比值。
%SNR = 10 * log10(sig_epsilon_range^2)
%当 sig_epsilon_range = 0.3 时，SNR ≈ 30 dB 当 sig_epsilon_range = 1 时，SNR ≈ 40 dB 当 sig_epsilon_range = 3 时，SNR ≈ 50 dB
%低噪、中噪、高噪
alpha_range = [0.9 1];     % path loss exponent  路径损耗指数
b_range = [90 100];        %global avg TX "level" (db)  全球平均发射功率水平（分贝）

sig_theta_range = [0.01,0.03,0.09];  % 信号角度范围
%sig_theta_range中的三个值分别为0.01、0.03和0.09，表示了三种不同的信号角度范围。较小的值表示信号角度范围较窄，即信号的传输方向相对集中。较大的值表示信号角度范围较宽，即信号的传输方向相对分散。
%通过在生成数据时使用不同的sig_theta值，可以模拟不同的信号角度环境。这样可以更好地评估和比较算法在不同信号角度条件下的性能和鲁棒性。


kappa = 0.21;  % kappa参数，用于生成空间相关的高斯随机场
%kappa参数用于生成空间相关的高斯随机场（GRF）。GRF是一种随机过程，用于建模空间中的随机变量，如图像或地理数据。
%在这里，kappa参数被用于生成空间相关的高斯随机场的协方差矩阵。协方差矩阵描述了随机变量之间的相关性和方差。kappa的值决定了GRF的空间相关性的程度。
%较小的kappa值会导致GRF的相关性较弱，即相邻像素之间的相关性较低。这意味着生成的随机场在空间上具有较大的变化和不规则性。
%较大的kappa值会导致GRF的相关性较强，即相邻像素之间的相关性较高。这意味着生成的随机场在空间上具有较为平滑和连续的变化。
%通过调整kappa值，可以控制生成的随机场的空间相关性，从而适应不同的应用需求和模拟场景。
areabounds = [0 5 0 5];    %size of the node traverse area (m) [xmin xmax ymin ymax]  节点遍历区域的大小（米）
imgorg = [0.5 0.5];        %lower left corner of the image [x y] (m)  图像的左下角坐标（米）
imgdims = [40 40];         %image size in pixels  图像的大小（像素）
pixelsize = 0.1;           %l/w of each square pixel (m)  每个正方形像素的长度/宽度（米）
dBwhite = 1;               %dB atten of a white pixel  白色像素的衰减（分贝）
wallcount_vec = [0 2 0 2 1 3]; %min/max for vertical , horizontal and square walls  垂直、水平和方形墙的最小/最大值
%表示垂直、水平和方形墙壁的最小和最大数量。这个向量中的值用来限制在区域内生成的墙壁的数量。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%preallocate data  预分配数据
K = imgdims(1)*imgdims(2);         %pixel count  像素数
N_Link = M*(M-1);                  %Number of UWB Links  UWB链路数
N_Tw = Tw^2;                       %number of UWB data per link  每个链路的UWB数据数
%每条链路连接连接两个节点，每个节点可以在6个航点上移动
x_1=0; y_1=0; 
x_2 = imgdims(2)*pixelsize+2*imgorg(1);      %UWB node range  UWB节点范围
y_2 = imgdims(1)*pixelsize+2*imgorg(2);
x_distance = (imgdims(2)-1)*pixelsize/(Tw-1);  %distance of two position of per node  每个节点两个位置之间的距离
y_distance = (imgdims(1)-1)*pixelsize/(Tw-1);
x_org = imgorg(1)+0.5*pixelsize;         %coordinate of first UWB node  第一个UWB节点的坐标
y_org = imgorg(2)+0.5*pixelsize;

% all coordinates of each node  每个节点的所有坐标
c = NaN(M,Tw);
for Twi = 1:Tw          %Tw point per node
    pos_node(1,Twi) = x_org + (Twi-1)*x_distance + 1j * y_1;
    pos_node(2,Twi) = x_2 + 1j * (y_org + (Twi-1)*y_distance);
    pos_node(3,Twi) = x_org + (Twi-1)*x_distance + 1j * y_2;
    pos_node(4,Twi) = x_1 + 1j * (y_org + (Twi-1)*y_distance);
end 

%通过 for 循环，对于每个节点，根据给定的参数计算节点的坐标，并将其存储在 pos_node 矩阵中。

%具体来说，对于每个节点，根据节点的索引 Twi 和给定的参数（x_org、y_org、x_distance、y_distance），计算出节点在不同路径点上的坐标。

%对于节点 1，其 x 坐标为 x_org + (Twi-1)*x_distance，y 坐标为 y_1。在这里，路径点是沿着 x 轴移动的。
%(0.55,0)	(1.33,0)	(2.11,0)	(2.89,0)	(3.67,0)	(4.45,0)
%对于节点 2，其 x 坐标为 x_2，y 坐标为 y_org + (Twi-1)*y_distance。在这里，路径点是沿着 y 轴移动的。
%(5,0.55)	(5,1.33)	(5,2.11)	(5,2.89)	(5,3.67)	(5,4.45)
%对于节点 3，其 x 坐标为 x_org + (Twi-1)*x_distance，y 坐标为 y_2。在这里，路径点是沿着 x 轴移动的。
%(0.55,5)	(1.33,5)	(2.11,5)	(2.89,5)	(3.67,5)	(4.45,5)
%对于节点 4，其 x 坐标为 x_1，y 坐标为 y_org + (Twi-1)*y_distance。在这里，路径点是沿着 y 轴移动的。
%(0,0.55)	(0,1.33)	(0,2.11)	(0,2.89)	(0,3.67)	(0,4.45)


%store the data  存储数据
nodepos = NaN(2,N_Tw,N_Link);     
%nodepos 是一个大小为 2 x N_Tw x N_Link 的矩阵，用于存储每个测量的UWB节点的位置。N_Tw代表每个节点的路径点数，N_Link代表链路的数量。
d = NaN(N_Link*N_Tw,1);                 %distance of UWB node for each measurements  每个测量的UWB节点间距离
W = NaN(N_Link*N_Tw,K);                 %weight of slf  slf的权重
W_ENR = NaN(N_Link*N_Tw,K);             %weight of slf for mismatched experiments  用于不匹配实验的slf权重
Z = zeros(N_Link*N_Tw,N_Link);          %weight of bias  偏置的权重

%node position calculation  节点位置计算
N_Linki = 0;
for i1 = 1:M
    for i2 = 1:M
        if i1 ~= i2
            N_Linki = N_Linki + 1;
            for Twi = 1:Tw
                nodepos(1,(Twi-1)*Tw+1:Twi*Tw,N_Linki)=pos_node(i1,Twi)*ones(1,Tw);
                nodepos(2,(Twi-1)*Tw+1:Twi*Tw,N_Linki)=pos_node(i2,:);
                %分别记录下对于每条链路，节点的位置
            end 
        end
    end
end 
%(Twi-1)Tw+1:TwiTw表示节点i1在nodepos矩阵中的位置索引范围。例如，当Twi=1时，索引范围为1:Tw；当Twi=2时，索引范围为Tw+1:2*Tw，依此类推。
%通过pos_node(i1,Twi)*ones(1,Tw)的赋值，将节点i1在路径点Twi上的坐标赋给了nodepos矩阵的第一个维度中指定的索引范围。这样，nodepos矩阵中的相应位置就存储了节点i1在不同路径点上的坐标信息。
%generate weight and distance  生成权重和距离
for N_Linki = 1:N_Link
    W((N_Linki-1)*N_Tw+1:N_Linki*N_Tw,:) = ...
        f_gen_Wi_ellipse(nodepos(:,:,N_Linki),pixelsize,imgorg,imgdims,1,2);
        % Inverse Area Elliptical Model:
        %B. R. Hamilton, X. Ma, R. J. Baxley, and S. M. Matechik, ‘‘Propagation
        %modeling for radio frequency tomography in wireless networks,   IEEE J.
        %Sel. Topics Signal Process., vol. 8, no. 1, pp. 55–65, Feb. 2014.
%     W((N_Linki-1)*N_Tw+1:N_Linki*N_Tw,:) = ...
%         f_gen_Wi(nodepos(:,:,N_Linki),pixelsize,imgorg,imgdims,1,2);     % Normalized Ellipse Model
    di = abs( nodepos(1,:,N_Linki) - nodepos(2,:,N_Linki) )';              %link lengths
%   使用abs函数计算向量差的绝对值，得到节点之间的距离（欧式距离）。
    d((N_Linki-1)*N_Tw+1:N_Linki*N_Tw,1) = 20 * log10( di );%将距离转换为分贝单位
    Z((N_Linki-1)*N_Tw+1:N_Linki*N_Tw,N_Linki) = ones(N_Tw,1);%将Z矩阵中对应链路的列设置为1，表示偏置的权重。
end 

C_theta = f_gen_C(imgdims,pixelsize,kappa);   % spatial correlated Gaussian random field
R_theta = chol(C_theta);  % 生成C_theta的上三角矩阵
%根据图像大小、像素大小和Kappa参数生成空间相关的高斯随机场，并进行Cholesky分解得到上三角矩阵。

逆面积椭圆模型

Inverse Area Elliptical Model:
Propagation Modeling for Radio Frequency Tomography in Wireless Networks

逆面积椭圆模型基于以下假设和原理：

假设无线电信号在传播过程中遵循自由空间传播模型。
假设目标区域的电磁波传播具有各向同性特性。
假设目标区域的电磁波传播路径可以近似为直线传播。
假设目标区域的电磁波传播路径与正常方向形成的夹角较小，使得传播路径可以近似为椭圆弧。

基于以上假设，逆面积椭圆模型的计算过程如下：

首先，根据图像的行数和列数确定像素总数K。
对于每个像素，计算像素相对于目标区域的椭圆中心的位置。
根据椭圆模型的公式计算像素的权重。权重的计算基于椭圆的半长轴、半短轴和椭圆弧的关系。通常使用的权重公式是根据椭圆的半长轴、半短轴和像素到椭圆中心的距离计算的。这个公式可以保证在椭圆中心处的权重最大，随着像素距离椭圆中心的距离增加，权重逐渐减小。
将计算得到的像素权重作为权重矩阵的一行，最终得到整个链路的权重矩阵。

论文中的逆面积椭圆模型的公式如下：

$X_{ij} = \frac{1}{{\pi u \sqrt{u^2 + d^2}}}$

其中， $X_{ij}$ 表示像素权重， $u$ 表示像素到椭圆中心的距离， $d$ 表示两个节点之间的距离。

通过这个公式，像素的权重与像素到椭圆中心的距离成反比。当像素越接近椭圆中心时，权重越大，反之，权重越小。这种权重计算方式可以更准确地反映无线电信号在像素上的传播强度。

与归一化椭圆模型相比，逆面积椭圆模型具有以下优势：

更准确的权重计算：逆面积椭圆模型考虑了像素到椭圆中心的距离，使得权重计算更加准确。这样可以更好地反映无线电信号在不同像素上的传播强度。
更好的图像质量：逆面积椭圆模型能够提供更高质量的成像结果。通过更准确的权重计算，可以减少成像中的噪声和伪像，提高图像的清晰度和准确性。
更好的目标定位和形状识别：逆面积椭圆模型能够更精确地定位目标区域，并提供更准确的形状识别。相比于归一化椭圆模型，逆面积椭圆模型能够更好地捕捉到目标区域的细节和边缘信息。

function [ Wi ] = f_gen_Wi_ellipse( nodepos, pixelsize, imgorg, imgdims, i1, i2 )
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% f_gen_Wi : GENERATE A WEIGHT MATRIX FOR THE ITH LINK (BIN) IN THE SYSTEM
% This function calls f_pixel_weights to compile all the relevant weights for all measurements taken
% between a given pair of nodes
% nodepos - array of node positions with time
% pixelsize - l/w of each square pixel (m)
% imgorg - [x y] position of lower left corner of image(m)
% imgdims - [rows cols] of the image
% i1 - node index of the TX, i2 - node index of the RX  (link i)
% Wi ( ni x K ) - weights for link i 
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

ni = size(nodepos,2); %# of time steps
K = imgdims(1)*imgdims(2); %pixel count

Wi = NaN(ni,K);
if i1 ~= i2 
    for j = 1:ni %loop over individual link's measurements
        p1 = [real(nodepos(i1,j)) imag(nodepos(i1,j))];
        p2 = [real(nodepos(i2,j)) imag(nodepos(i2,j))];
        Wi(j,:) = f_pixel_weights_3(imgdims,pixelsize,imgorg,p1,p2);
    end
else
    Wi = zeros(ni,K); %invalid link
end

end

function Xij = f_pixel_weights_3(imgdims, pixelsize, imgorg, p1, p2)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% COMPUTES THE PIXEL WEIGHTS FOR SINGLE MEASUREMENT J OF LINK I (tomographic projection) %
% Xij (1 x numpixels) - row vector of weights for the given points. inverse area ellipse %
% imgdims (1x2) - number of [rows cols] in the image. the image is assumed to reside in  %
%   the first quadrant, with the lower left corner at the origin                         %
% pixelsize - the PHYSICAL length of a pixel's sides, assumed to be square pixels (m)    %
% imgorg (1x2) - physical [x y] location of the lower left corner of the image (m)       %
% p1, p2 (1x2) - [x y] locations of the two nodes of interest (m)                        %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% inverse area ellipse model

freq_RF = 2.4e9;  % RF 2.4 GHz
lanpt = 3e8/freq_RF;    %wave length

p1 = p1' - imgorg';
p2 = p2' - imgorg'; %scale points to "single units"
fai = (p1-p2)/norm(p1-p2);   %projection vector
c = (p1+p2)/2;               % center of the ellipse
d = norm(p1-p2);

K = imgdims(1)*imgdims(2); %pixel count
bb = zeros(1,K);
u = NaN(1,K);
u_max = 0.5*sqrt(1*lanpt*d);

NI = 0;
for j=1:imgdims(2)   %col
    for i=1:imgdims(1)   %row
        NI = NI + 1;          % number of pixels
        sx = (j-0.5)*pixelsize;
        sy = (imgdims(1)-i+0.5)*pixelsize;
        px = fai(1)*(sx-c(1))+fai(2)*(sy-c(2));
        py = -fai(2)*(sx-c(1))+fai(1)*(sy-c(2));
        a0 = 1; b0 = -(px^2+py^2-d^2); c0 = -py^2*d^2;
        u_2 = (-b0 + sqrt(b0^2-4*a0*c0))/(2*a0);
        u(1,NI) = sqrt(u_2);
        if u(1,NI)<u_max
            if u(1,NI)<0.05
                u(1,NI) = 0.05;
            end
            bb(1,NI) = 1/(pi*u(1,NI)*sqrt(u(1,NI)^2+d^2));
        end
    end 
end
Xij = bb;
% imshow(reshape(Xij,[40,40]),[0 max(Xij)])

% %DEBUG plot code

end

根据代码中的变量和计算过程，用数学公式来具象化一下代码中的中间变量：

投影向量fai：

$\mathbf{fai} = \frac{\mathbf{p1} - \mathbf{p2}}{\|\mathbf{p1} - \mathbf{p2}\|}$

投影向量fai表示从节点p1指向节点p2的方向向量。它的物理含义是两个节点之间的传播方向。
椭圆中心c：

$\mathbf{c} = \frac{\mathbf{p1} + \mathbf{p2}}{2}$

椭圆中心c表示节点p1和节点p2之间的中心位置，两个节点之间传播路径的中心点。
两个节点之间的距离d：

$\|\mathbf{p1} - \mathbf{p2}\|$

两个节点之间的距离d表示节点p1和节点p2之间的物理距离。表示两个节点之间的传播路径的长度。
像素的物理坐标 $(x, y)$ ：

$\times \text{pixelsize}$
$(\text{imgdims}(1) - i + 0.5) \times \text{pixelsize}$

像素的物理坐标表示像素在图像中的具体位置。其中，j表示列索引，i表示行索引。这些公式根据像素的索引和像素大小将像素的位置转换为物理坐标。
像素相对于椭圆中心的位置(px, py)：

$\text{px} = \mathbf{fai}(1) \times (x - c(1)) + \mathbf{fai}(2) \times (y - c(2))$
$\text{py} = -\mathbf{fai}(2) \times (x - c(1)) + \mathbf{fai}(1) \times (y - c(2))$

像素相对于椭圆中心的位置表示像素相对于椭圆中心的偏移量。
计算权重的中间变量u：

$a_0 = 1$
$b_0 = -(\text{px}^2 + \text{py}^2 - d^2)$
$c_0 = -\text{py}^2 \times d^2$
$u_2 = \frac{-b_0 + \sqrt{b_0^2 - 4a_0c_0}}{2a_0}$
$\sqrt{u_2}$

这些中间变量用于计算像素的权重。它们基于椭圆模型的方程来计算像素的权重。通过计算像素相对于椭圆中心的位置和椭圆模型的公式，可以得到中间变量u。
计算像素的权重bb：

如果 $u < 0.05$ ，则 $u = 0.05$ 。
这是为了避免u过小导致权重计算出现除以接近于零的值的情况。当u值非常接近于零时，权重计算公式中的分母会接近于零，这可能会导致除法运算产生无穷大或非常大的值。为了避免这种情况，代码中将u的最小值限制为0.05。将u设置为0.05是一种经验性的做法，目的是确保权重计算的稳定性和可靠性。通过将u的最小值设置为一个较小的值，可以避免权重计算过程中出现数值不稳定的情况，并确保计算得到的权重在合理的范围内。这样可以提高无线电频率层析成像的准确性和稳定性
$\text{bb}(NI) = \frac{1}{\pi u \sqrt{u^2 + d^2}}$

像素的权重bb表示像素的相对重要性或传播强度。它的物理含义是像素在传播路径中的权重，即像素对于目标成像的贡献程度。