模型评估
在进行回归和分类时,为了进行预测,我们定义了函数 f θ ( x ) f_\theta(x) fθ(x),然后根据训练数据求出了函数的参数 θ \theta θ。
如何预测函数 f θ ( x ) f_\theta(x) fθ(x)的精度?看它能否很好的拟合训练数据?
我们需要能够定量的表示机器学习模型的精度,这就是模型的评估。
交叉验证
回归问题的验证
把获取的全部训练数据分成两份:一份用于测试,一份用于训练。前者来评估模型。一般3:7或者2:8这种训练数据更多的比例。
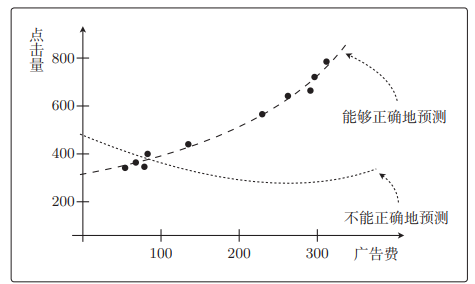
如图点击量预测的回归问题
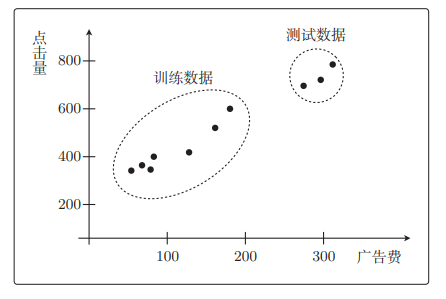
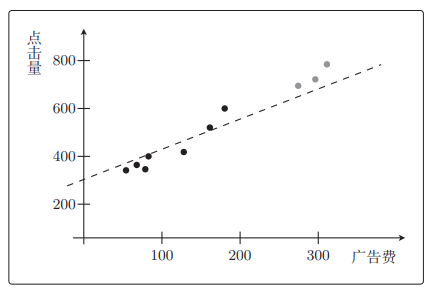
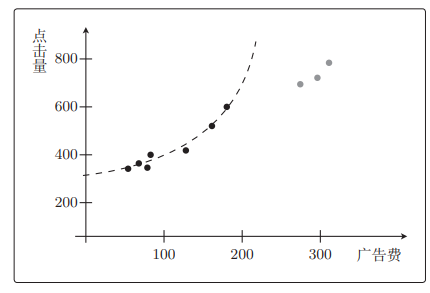
f θ ( x ) f_\theta(x) fθ(x)是二次函数拟合效果更好,但考虑测试数据的话,二次函数完全不行。
对于回归,只要在训练好的模型上计算测试数据的误差的平方,再取其平均值即可,假设训练数据有
n
n
n个,可以这样计算。
1
n
∑
i
=
1
n
(
y
(
i
)
−
f
θ
(
x
(
i
)
)
)
2
\frac1n\sum\limits_{i=1}^n(y^{(i)}-f_\theta(x^{(i)}))^2
n1i=1∑n(y(i)−fθ(x(i)))2
对于点击量的回归问题,
y
(
i
)
y^{(i)}
y(i)就是点击量,
x
(
i
)
x^{(i)}
x(i)就是广告费。
这个值被称为均方误差或者MSE(Mean Square Error)
这个误差越小,精度就越高,模型就越好。
分类问题的验证
数据这样分配
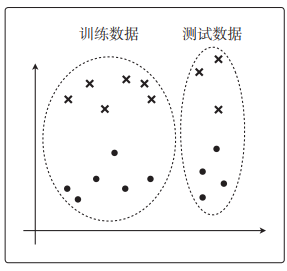
θ T x \theta^Tx θTx是一次函数
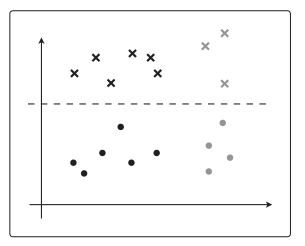
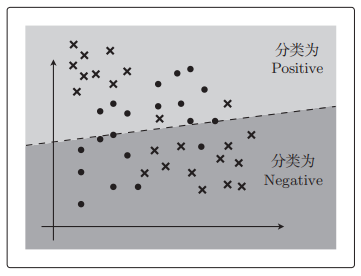
若 θ T x \theta^Tx θTx更复杂,可能会这样紧贴着训练数据进行分类。
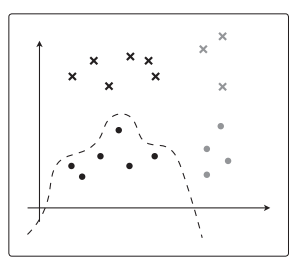
我们是根据图像为横向的概率来分类,分类是否成功就会有下面 4 种情况。
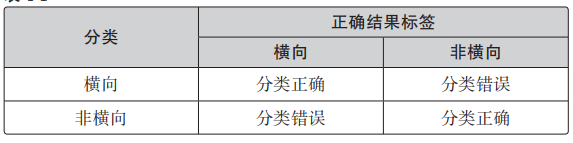
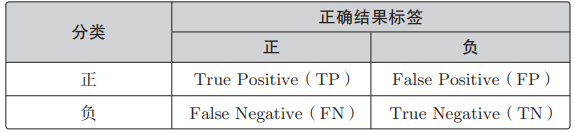
可以这样计算分类的精度
A c c u r a c y = T P + T N T P + F P + F N + T N Accuracy=\frac{TP+TN}{TP+FP+FN+TN} Accuracy=TP+FP+FN+TNTP+TN
它表示的是在整个数据集中,被正确分类的数据 T P TP TP和 T N TN TN所占的比例。
精确率和召回率
有时候只看 A c c u r a c y Accuracy Accuracy会出问题
如果数据量极其不平衡
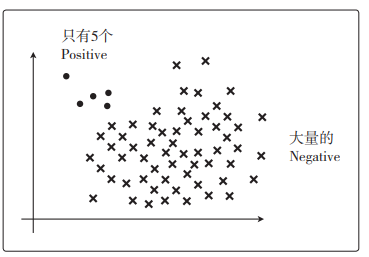
模型把全部数据分类为 Negative,不是好模型,但精度会很高。
所以我们加入别的指标
精确率
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
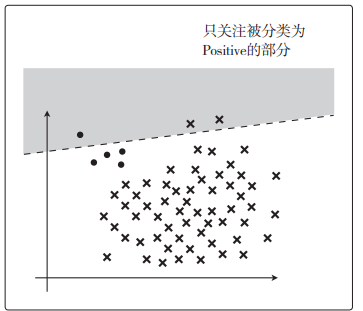
这个指标只关注 TP 和 FP。根据表达式来看,它的含义是在被分类为 Positive 的数据中,实际就是 Positive 的数据所占的比例
召回率
R e c a l l = T P T P + F N Recall=\frac{TP}{TP+FN} Recall=TP+FNTP
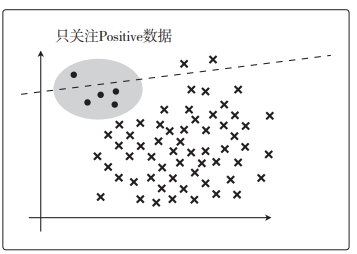
这个指标只关注 TP 和 FN。根据表达式来看,它的含义是在 Positive 数据中,实际被分类为 Positive 的数据所占的比例
基于这两个指标来考虑精度比较好。
但是一个高一个低就不好评估,为此出现判定综合性能的指标F值。
F m e a s u r e = 2 1 P r e c i s i o n + 1 R e c a l l Fmeasure=\frac{2}{\frac{1}{Precision}+\frac1{Recall}} Fmeasure=Precision1+Recall12
变形后
F m e a s u r e = 2 ⋅ P r e c i s i o n ⋅ R e c a l l P r e c i s i o n + R e c a l l Fmeasure=\frac{2\cdot Precision\cdot Recall}{Precision+Recall} Fmeasure=Precision+Recall2⋅Precision⋅Recall
F值称为F1值更准确
还有带权重的F值指标
W e i g h t e d F m e a s u r e = ( 1 + β 2 ) ⋅ P r e c i s i o n ⋅ R e c a l l β 2 ⋅ P r e c i s i o n + R e c a l l WeightedFmeasure=\frac{(1+\beta^2)\cdot Precision\cdot Recall}{\beta^2\cdot Precision+Recall} WeightedFmeasure=β2⋅Precision+Recall(1+β2)⋅Precision⋅Recall
之前的精确率和召回率是以 T P TP TP为主进行计算的,也可以以TN为主。
P r e c i s i o n = T N T N + F N Precision=\frac{TN}{TN+FN} Precision=TN+FNTN
R e c a l l = T N T N + F P Recall=\frac{TN}{TN+FP} Recall=TN+FPTN
把全部训练数据分为测试数据和训练数据的做法称为交叉验证
交叉验证中,尤为有名的是K折交叉验证
- 把全部训练数据分为 K K K 份
- 将 K − 1 K − 1 K−1 份数据用作训练数据,剩下的 1 份用作测试数据
- 每次更换训练数据和测试数据,重复进行 K K K 次交叉验证
- 最后计算 K K K 个精度的平均值,把它作为最终的精度
假设进行4折交叉验证,那么就会如图这样测试精度。
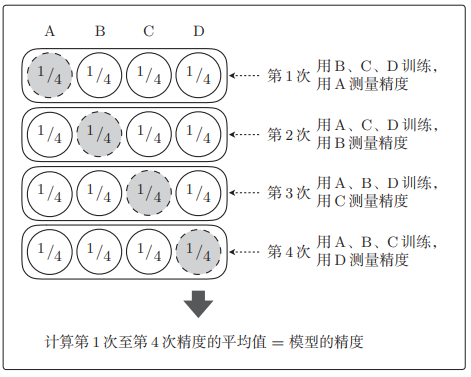
全部训练数据的量很大,不切实际增大 K K K值会非常耗时,要确定一个合适的 K K K值。
正则化
过拟合
只能拟合训练数据的状态被称为过拟合
有几种方法可以避免过拟合
- 增加全部训练数据的数量
- 使用简单的模型
- 正则化
正则化的方法
对于回归问题
E ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) 2 E(\theta)=\frac12\sum\limits_{i=1}^n(y^{(i)}-f_\theta(x^{(i)})^2 E(θ)=21i=1∑n(y(i)−fθ(x(i))2
向这个目标函数增加一个正则化项
R ( θ ) = λ 2 ∑ j = 1 m θ j 2 R(\theta)=\frac\lambda2\sum\limits_{j=1}^m\theta_j^2 R(θ)=2λj=1∑mθj2 ( m m m是参数的个数)
一般不对 θ 0 \theta_0 θ0应用正则化,假如预测函数的表达式为 f θ ( x ) = θ 0 + θ 1 x + θ 2 x 2 f_\theta(x)=\theta_0+\theta_1x+\theta_2x^2 fθ(x)=θ0+θ1x+θ2x2, m = 2 m=2 m=2意味着正则化的对象参数为 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2。 θ 0 \theta_0 θ0这种只有参数的项为偏置项,一般不对它进行正则化。
λ \lambda λ是决定正则化项影响程度的正的常数。
C ( θ ) = 1 2 ∑ i = 1 n ( y ( i ) − f θ ( x ( i ) ) 2 C(\theta)=\frac12\sum\limits_{i=1}^n(y^{(i)}-f_\theta(x^{(i)})^2 C(θ)=21i=1∑n(y(i)−fθ(x(i))2
R ( θ ) = λ 2 ∑ j = 1 m θ j 2 R(\theta)=\frac\lambda2\sum\limits_{j=1}^m\theta_j^2 R(θ)=2λj=1∑mθj2
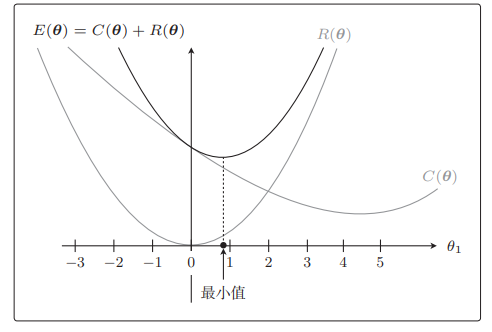
这正是通过减小不需要的参数的影响,将复杂模型替换为简单模型来防止过拟合的方式。
为了防止参数的影响过大,在训练时要对参数施加一些惩罚。
λ \lambda λ是控制正则化惩罚的强度。
λ = 0 \lambda=0 λ=0,相当于不使用正则化。
λ \lambda λ越大,正则化的惩罚就越严厉。
分类的正则化
l o g L ( θ ) = ∑ i = 1 n ( y ( i ) l o g f θ ( x i ) + ( 1 − y ( i ) ) l o g ( 1 − f θ ( x ( i ) ) ) ) logL(\theta)=\sum\limits_{i=1}^n(y^{(i)}logf_\theta(x^{i}) +({1-y^{(i)}})log(1-f_\theta(x^{(i)}))) logL(θ)=i=1∑n(y(i)logfθ(xi)+(1−y(i))log(1−fθ(x(i))))
分类也是在这个目标函数中增加正则化项就行了。
l o g L ( θ ) = − ∑ i = 1 n ( y ( i ) l o g f θ ( x i ) + ( 1 − y ( i ) ) l o g ( 1 − f θ ( x ( i ) ) ) ) + λ 2 ∑ j = 1 m θ j 2 logL(\theta)=-\sum\limits_{i=1}^n(y^{(i)}logf_\theta(x^{i}) +({1-y^{(i)}})log(1-f_\theta(x^{(i)})))+\frac\lambda2\sum\limits_{j=1}^m\theta_j^2 logL(θ)=−i=1∑n(y(i)logfθ(xi)+(1−y(i))log(1−fθ(x(i))))+2λj=1∑mθj2
对数似然函数本来以最大化为目标,加负号使其变为和回归的目标函数一样的最小化问题,像处理回归一样处理它,只要加上正则化项就可以了。
包含正则化项的表达式的微分
E ( θ ) = C ( θ ) + R ( θ ) E(\theta)=C(\theta)+R(\theta) E(θ)=C(θ)+R(θ)
各部分进行偏微分
∂
E
(
θ
)
∂
θ
j
=
∂
C
(
θ
)
∂
θ
j
+
∂
R
(
θ
)
∂
θ
j
\frac{\partial E(\theta)}{\partial\theta_j}= \frac{\partial C(\theta)}{\partial\theta_j}+ \frac{\partial R(\theta)}{\partial\theta_j}
∂θj∂E(θ)=∂θj∂C(θ)+∂θj∂R(θ)
∂
C
(
θ
)
∂
θ
j
=
∑
i
=
1
n
(
f
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
\frac{\partial C(\theta)}{\partial\theta_j}=\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
∂θj∂C(θ)=i=1∑n(fθ(x(i))−y(i))xj(i)
∂ R ( θ ) ∂ θ j = λ θ j \frac{\partial R(\theta)}{\partial\theta_j}=\lambda\theta_j ∂θj∂R(θ)=λθj
∂ E ( θ ) ∂ θ j = ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ θ j \frac{\partial E(\theta)}{\partial\theta_j}=\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+\lambda\theta_j ∂θj∂E(θ)=i=1∑n(fθ(x(i))−y(i))xj(i)+λθj
得参数更新表达式
θ j : = θ j − η ( ∑ i = 1 n ( f θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ θ j ) \theta_j:=\theta_j-\eta(\sum\limits_{i=1}^n(f_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+\lambda\theta_j) θj:=θj−η(i=1∑n(fθ(x(i))−y(i))xj(i)+λθj) ( j > 0 ) (j>0) (j>0)
这种方法叫L2正则化
还有L1正则化,它的正则化项 R R R是
R ( θ ) = λ ∑ i = 1 m ∣ θ i ∣ R(\theta)=\lambda\sum\limits_{i=1}^m|\theta_i| R(θ)=λi=1∑m∣θi∣
L1 正则化的特征是被判定为不需要的参数会变为 0,从而减少变量个数。而 L2 正则化不会把参数变为 0。二次式变为一次式的例子,用 L1 正则化就真的可以实现了。
L2 正则化会抑制参数,使变量的影响不会过大,而 L1 会直接去除不要的变量。
学习曲线
欠拟合:模型性能很差,没有拟合训练数据的状态
区分过拟合与欠拟合
两种精度都是很差,如何辨别?
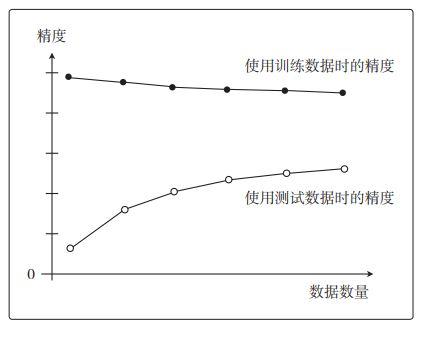
随着数据量的增加,使用训练数据时的精度一直很高,而使用测试数据时的精度一直没有上升到它的水准。只对训练数据拟合得较好,这就是过拟合的特征。
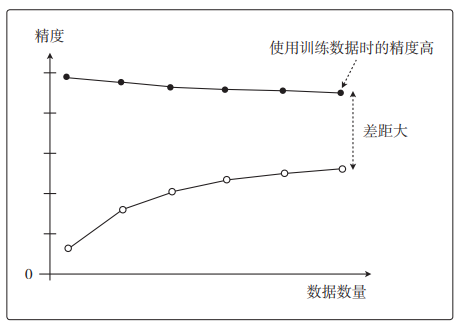
这也叫作高方差。
欠拟合的图像如下
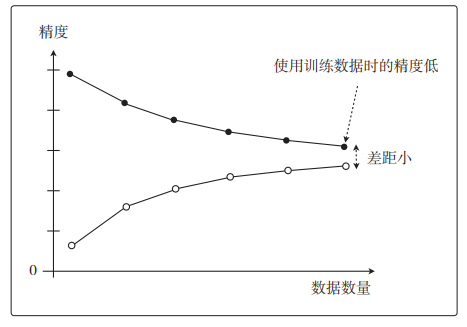
这是一种即使增加数据的数量,无论是使用训练数据还是测试数据,精度也都会很差的状态。
像这样展示了数据数量和精度的图称为学习曲线