题目 

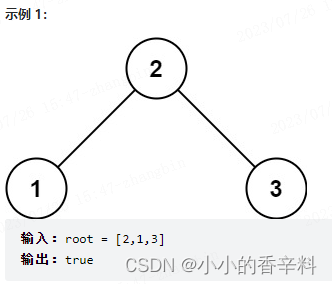
给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

思路

最开始想简单了，简单的以为只要满足左右孩子存在且左孩子大于等于root 或者 右孩子存在且右孩子小于等于root，就返回False，如果遇到空节点，说明以root为跟的树是二叉排序树。因为如果不是二叉排序树，那么从根节点出发，走到空节点之前就应该返回False了，根本不会出现空的情况。但这个错误在于它只会保持每三子节点组成的小结构是有序的，但整体不保证有序。

比如这个样例：[5,4,6,null,null,3,7]，按照我的逻辑是true，因为对于每一个节点与它的左右孩子都是有序的，但是整体并不是有序的，应该返回false。

以下是错误代码示例：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        if (root.left and root.left.val>=root.val) or (root.right and root.val>=root.right.val):
            return False
        left = self.isValidBST(root.left)
        right = self.isValidBST(root.right)
        return left and right

正确思路是利用二叉排序树中序遍历序列是有序这个特性去做，弄一个self.max_记录当前节点之前的最大值，然后不断更新，如果发现当前节点<=self.max_说明这棵树不是二叉排序树，否则继续递归遍历，知道节点为空返回true。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def __init__(self):
        self.max_ = float('-inf')
        
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if not root:
            return True
        left = self.isValidBST(root.left)
        if self.max_>=root.val:
            return False
        else:
            self.max_ = root.val
        right = self.isValidBST(root.right)
        return left and right