1. 解决了什么问题?
预测定位质量对于目标检测很重要,在 NMS 时它能提供准确的得分排序,提高模型的表现。现有方法都是通过分类或回归的卷积特征来预测定位质量得分。
2. 提出了什么方法?
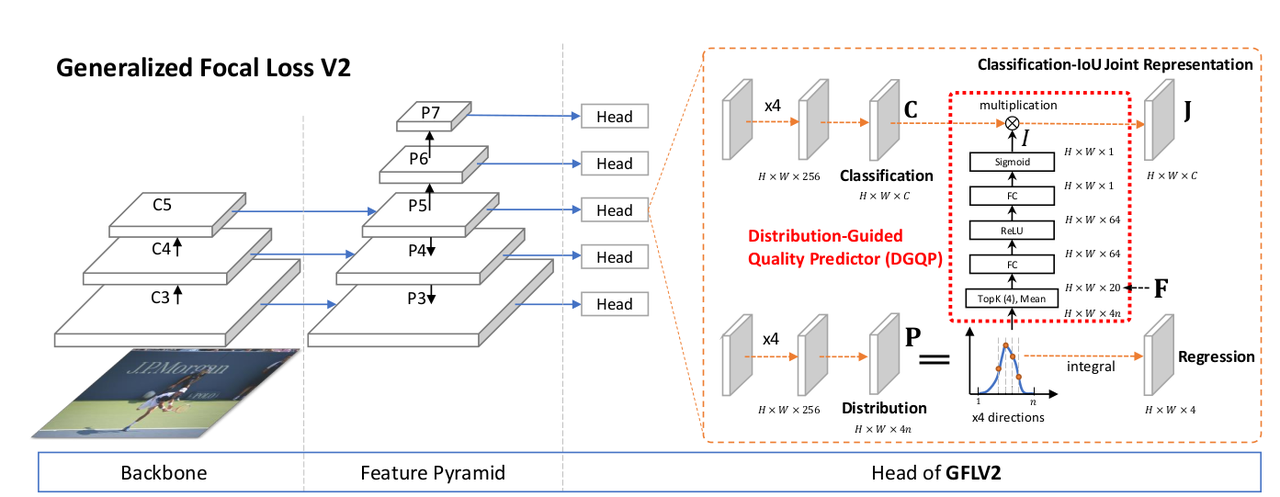
受到 GFLv1 的 general distribution 启发,本文提出基于边框的 { l , r , t , b } \lbrace l,r,t,b\rbrace {l,r,t,b}四个参数的分布来学习定位质量预测。边框分布如果是尖锐的,则其定位质量就高。边框分布的统计和真实定位质量之间具有紧密的关系,于是作者设计了 distribution-guided quality predictor,它学习每条预测边离散的概率分布。下图(b) 反映的是预测框 general distribution 的最大值(四条边的均值)和真实定位质量(IoU)之间的关系。

2.1 GFLv1
提出了分类-IoU 联合表征,减轻定位质量预测和分类预测在训练和推理时不一致的问题。给定一个类别为
c
∈
{
1
,
2
,
.
.
.
,
m
}
c\in \lbrace 1,2,...,m\rbrace
c∈{1,2,...,m}的目标,GFLv1 使用分类分支输出类别与 IoU 的联合表征
J
=
[
J
1
,
J
2
,
.
.
.
,
J
m
]
\mathbf{J}=\left[J_1,J_2,...,J_m\right]
J=[J1,J2,...,Jm],满足:
J
i
=
{
IoU
(
b
p
r
e
d
,
b
g
t
)
,
if
i
=
c
0
,
otherwise
J_i = \left\{ \begin{array}{ll} \text{IoU}(b_{pred}, b_{gt}),\quad\text{if}\quad i=c \\ 0,\quad\quad\quad\quad\quad\quad \text{otherwise} \end{array} \right.
Ji={IoU(bpred,bgt),ifi=c0,otherwise
边框表征的 General Distribution
现有的检测器通常使用 Dirac Delta 分布建模边框回归问题: y = ∫ − ∞ + ∞ δ ( x − y ) x d x y=\int_{-\infty}^{+\infty}\delta(x-y)x \mathop{dx} y=∫−∞+∞δ(x−y)xdx。GFLv1 提出的 General Distribution P ( x ) P(x) P(x)将每条边表示为 y ^ = ∫ − ∞ + ∞ P ( x ) x d x = ∫ y 0 y n P ( x ) x d x \hat{y}=\int_{-\infty}^{+\infty}P(x)x \mathop{dx}=\int_{y_0}^{y_n}P(x)x \mathop{dx} y^=∫−∞+∞P(x)xdx=∫y0ynP(x)xdx。再从连续域转化为离散域 [ y 0 , y 1 , . . . , y i , y i + 1 , . . . , y n − 1 , y n ] \left[y_0,y_1,...,y_i,y_{i+1},...,y_{n-1},y_n \right] [y0,y1,...,yi,yi+1,...,yn−1,yn],等间距为 Δ = y i + 1 − y i , ∀ i ∈ { 0 , 1 , . . . , n − 1 } \Delta=y_{i+1}-y_i,\forall i\in \lbrace0,1,...,n-1\rbrace Δ=yi+1−yi,∀i∈{0,1,...,n−1}。根据离散分布的性质 ∑ i = 0 n P ( y i ) = 1 \sum_{i=0}^n P(y_i)=1 ∑i=0nP(yi)=1, y ^ \hat{y} y^的预测回归值为:
y
^
=
∑
i
=
0
n
P
(
y
i
)
y
i
\hat{y}=\sum_{i=0}^n P(y_i)y_i
y^=i=0∑nP(yi)yi
如上图© 和 (d) 所示,与 Dirac Delta 分布相比,General Distribution 能更好地反映边框的预测质量。
2.2 GFLv2
Decomposed Classification-IoU Representation
尽管联合表征解决了目标分类和定位质量预测在训练和推理时不一致的问题,但它仍有缺陷,因为只用了分类分支预测的联合表征。本文方法则直接利用分类分支(
C
\mathbf{C}
C)和回归分支(
I
I
I)的信息:
J
=
C
×
I
\mathbf{J}=\mathbf{C}\times I
J=C×I
C = [ C 1 , C 2 , . . . , C m ] , C i ∈ [ 0 , 1 ] \mathbf{C}=\left[C_1,C_2,...,C_m\right],C_i\in \left[0,1\right] C=[C1,C2,...,Cm],Ci∈[0,1]表示 m m m个类别的分类表征。 I ∈ [ 0 , 1 ] I\in \left[0,1\right] I∈[0,1]是一个标量,表示 IoU 表征。
尽管 J \mathbf{J} J拆分为两个部分,但在训练和推理时只用 J \mathbf{J} J。 C \mathbf{C} C来自于分类分支, I I I来自于回归分支的 DGQP。训练时 J \mathbf{J} J用 QFL 进行监督,推理时直接作为 NMS 的得分使用。
DGQP
DGQP 将学到的 general distribution P \mathbf{P} P输入一个子网络,得到预测的 IoU 标量 I I I,辅助生成 J \mathbf{J} J。用位置到目标框四条边的相对偏移量作为回归目标,由 general distribution 表示。用 { l , r , t , b } \lbrace l,r,t,b\rbrace {l,r,t,b}表示四条边,用 P w = [ P w ( y 0 ) , P w ( y 1 ) , . . . , P w ( y n ) ] , w ∈ { l , r , t , b } \mathbf{P}^w=\left[P^w(y_0),P^w(y_1),...,P^w(y_n)\right], w\in \lbrace l,r,t,b\rbrace Pw=[Pw(y0),Pw(y1),...,Pw(yn)],w∈{l,r,t,b}表示各边的离散概率。
如上图所示,学到的分布与最终检测框的质量是高度相关的,可以用一些统计数字表示 general distribution 的平坦程度。这些统计特征与定位质量高度相关,能降低训练的难度、提升预测的质量。从每个分布向量 P w \mathbf{P}^w Pw中选取 top-k 个值及其均值,将它们 concat 产生基础统计特征 F ∈ R 4 ( k + 1 ) \mathbf{F}\in \mathbb{R}^{4(k+1)} F∈R4(k+1):
F = Concat ( { Topkm ( P w ) ∣ w ∈ { l , r , t , b } } ) \mathbf{F}=\text{Concat}(\lbrace \text{Topkm}(\mathbf{P}^w) | w\in \lbrace l,r,t,b\rbrace\rbrace) F=Concat({Topkm(Pw)∣w∈{l,r,t,b}})
Topkm ( ⋅ ) \text{Topkm}(\cdot) Topkm(⋅)表示 top-k 个值和均值的联合操作。 Concat ( ⋅ ) \text{Concat}(\cdot) Concat(⋅)表示通道 concat。选取 top-k 个值和均值作为输入统计有两个好处:
- 因为 P w \mathbf{P}^w Pw是固定的, ∑ i = 0 n P w ( y i ) = 1 \sum_{i=0}^n P^w(y_i)=1 ∑i=0nPw(yi)=1,top-k 个值和均值基本上反映了分布的平坦程度:值越大,分布越尖锐;值越小,分布越平坦。
- 如下图,top-k 值和均值能让统计特征在分布域内,对相对偏移量不敏感,表征就不易受目标尺度的影响,更加鲁棒。
[图片]
将 general distribution 的统计特征 F \mathbf{F} F作为输入,作者设计了一个微型网络 F ( ⋅ ) \mathcal{F}(\cdot) F(⋅)来预测 IoU 质量得分。该网络有 2 个全连接层,后面分别跟着 ReLU \text{ReLU} ReLU和 Sigmoid \text{Sigmoid} Sigmoid。 I I I的计算如下:
I = F ( F ) = σ ( W 2 δ ( W 1 F ) ) I=\mathcal{F}(\mathbf{F})=\sigma(\mathbf{W}_2 \delta(\mathbf{W}_1 \mathbf{F})) I=F(F)=σ(W2δ(W1F))
δ , σ \delta,\sigma δ,σ分别是 ReLU \text{ReLU} ReLU和 Sigmoid \text{Sigmoid} Sigmoid函数。 W 1 ∈ R p × 4 ( k + 1 ) \mathbf{W}_1\in \mathbb{R}^{p\times 4(k+1)} W1∈Rp×4(k+1)和 W 2 ∈ R 1 × p \mathbf{W}_2 \in \mathbb{R}^{1\times p} W2∈R1×p。实验时, k = 4 k=4 k=4表示 top-k 的参数, p = 64 p=64 p=64是隐藏层的通道数。
GFLv2 的整体结构如下图所示。DGQP 非常轻量。它只增加了几千个参数,对于模型 ResNet-50 和 FPN,DGQP 的参数量只占 ∼ 0.003 % \sim0.003\% ∼0.003%,不会降低训练和推理速度。