文章目录
- 一、过拟合与欠拟合
- 1 过拟合
- 1.1 线性回归的过拟合
- 1.2 过拟合和正则项
- 1.2.1 带有L2正则化的线性回归—Ridge回归
- 1.2.2 带有L1正则化的线性回归—LASSO回归
- 1.2.3 Ridge(L2-norm)和LASSO(L1-norm)比较
- 1.2.4 Elasitc Net
- 2 欠拟合
- 3 用法(梯度下降、坐标轴下降法)
一、过拟合与欠拟合
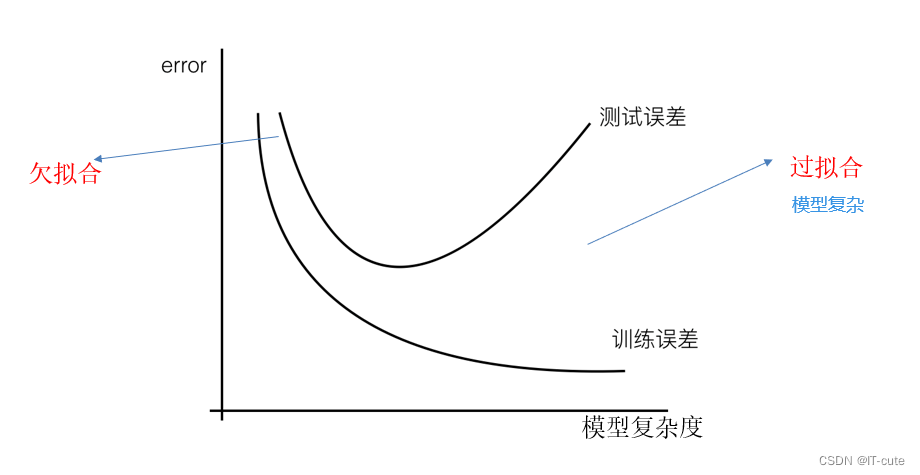
1 过拟合
**过拟合:**一个假设在训练数据上能够获得比其他假设更好的拟合, 但是在训练数据外的数据集上却不能很好地拟合数据,此时认为这个假设出现了过拟合的现象。(模型过于复杂)
多项式扩展的时候,如果指定的阶数比较大,那么有可能导致过拟合。从线性回归模型中来讲,我们认为训练出来的模型参数值越大,就表示越存在过拟合的情况。
原因:原始特征过多,存在一些嘈杂特征, 模型过于复杂是因为模型尝试去兼顾各个测试数据点
解决办法:
- 进行特征选择,消除关联性大的特征(很难做)
- 交叉验证(让所有数据都有过训练)
- 正则化(了解)
为了解决过拟合问题:我们可以选择在损坏函数中加入惩罚项(对于系数过大的惩罚),主要分为L1-norm和L2-norm。
1.1 线性回归的过拟合

1.2 过拟合和正则项
引入了 正则化 概念。

直观上来看,如果我们想要解决上面回归中的过拟合问题,我们最好就要消除X3和X4的影响,也就是想让θ3,θ4都等于0,一个简单的方法就是我们对θ3,θ4进行惩罚,增加一个很大的系数,这样在优化的过程中就会使这两个参数为零。
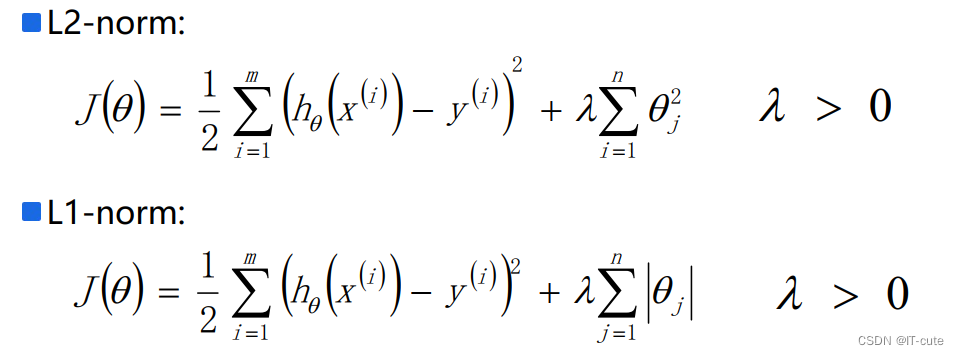
1.2.1 带有L2正则化的线性回归—Ridge回归
使用L2正则的线性回归模型就称为Ridge回归(岭回归)
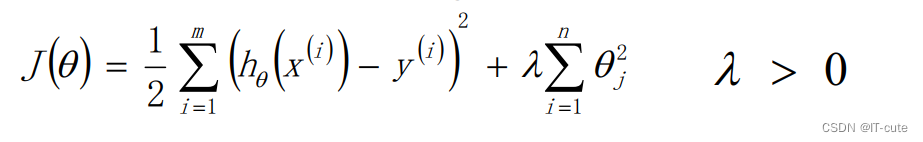
岭回归:回归得到的回归系数更符合实际,更可靠。另外,能让估计参数的波动范围变小,变的更稳定。在存在病态数据(异常数据)偏多的研究中有较大的实用价值。
1.2.2 带有L1正则化的线性回归—LASSO回归
使用L1正则的线性回归模型就称为LASSO回归(Least Absolute Shrinkage and Selection Operator)
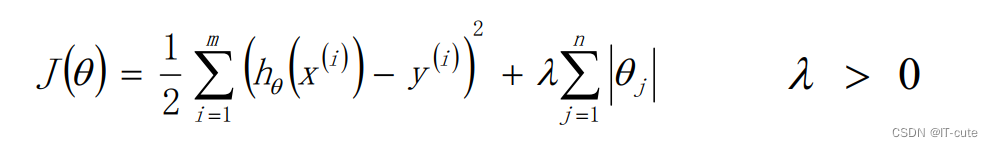
1.2.3 Ridge(L2-norm)和LASSO(L1-norm)比较
- L2-norm中,由于对于各个维度的参数缩放是在一个圆内缩放的,不可能导致有维度参数变为0的情况,那么也就不会产生稀疏解;实际应用中,数据的维度中是存在噪音和冗余的,稀疏的解可以找到有用的维度并且减少冗余,提高回归预测的准确性和鲁棒性(减少了overfitting)(L1-norm可以达到最终解的稀疏性的要求)
- Ridge模型具有较高的准确性、鲁棒性以及稳定性;LASSO模型具有较高的求解速度。
- 如果既要考虑稳定性也考虑求解的速度,就使用Elasitc Net
1.2.4 Elasitc Net
同时使用L1正则和L2正则的线性回归模型就称为Elasitc Net算法(单性网络算法)
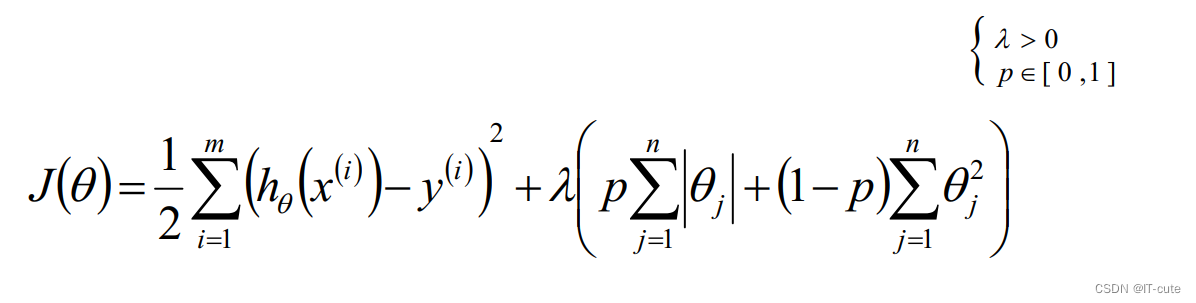
2 欠拟合
**欠拟合:**一个假设在训练数据上不能获得更好的拟合, 但是在训练数据外的数据集上也不能很好地拟合数据,此时认为这个假设出现了欠拟合的现象。(模型过于简单)
原因:学习到数据的特征过少
解决办法:增加数据的特征数量
3 用法(梯度下降、坐标轴下降法)
- 只要且标函数是凸函数,就使用梯度下降—>普通的线性回归和L2-norm线性回归
- 坐标轴下降法—>L1-norm