一、题目描述

给你一个二叉树的根节点 root ， 检查它是否轴对称。

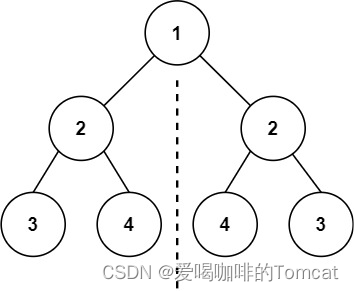
输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

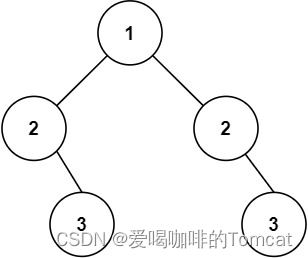
输入：root = [1,2,2,null,3,null,3]
输出：false

二、代码思路

详细题解地址

思路有两种递归和迭代：

比较树是否对称，其实就是比较根节点的两颗子树是否对称，那么两棵子树是否对称的依据很有特点：

• left子树的left节点与right子树的right节点相等。
• left子树的right节点与right子树的left节点相等。
• 树的结构就是递归的结构，所以上述判断可以针对所有子树来说。

如此，就产生了递归和迭代两种方法去实现，迭代很容易理解。

需要借助队列，将根节点的左右节点装入队列，弹出并判断是否相等，然后将left节点的left 与 right节点的right装入队列，其次left子树的right节点与right子树的left节点装入队列。进行新一轮判断。

递归相比迭代比较难理解，但是跟树的递归模板类似：

• 定义本层逻辑，包括本层的处理逻辑，本层的退出逻辑。
  • 退出逻辑： 节点都为空、节点有一个为空、节点值不等。
  • 本层处理逻辑：处理逻辑就是与题目相关，判断是否退出与是否进入下一层的逻辑。
• 递归的调用下一层，传入的参数是由本层逻辑确定的，一般都是子树节点。
  • 两个节点值相同就进入下一层。

模板如下：

private boolean dfs(TreeNode left, TreeNode right) {
        //左右节点都为null
        if (left == null && right == null) {
            return true;
        //左右节点都不为空
        } else if (left != null && right != null) {
            //如果两者相等，那么镜像地判断其孩子节点
            if (left.val == right.val) {
                return dfs(left.left,right.right) && dfs(left.right, right.left);
            } else {
                //如果不同，则返回false
                return false;
            }
        } else {
            //左右节点有一为空 有一不为空
            return false;
        }
    }

三、代码题解

package leetcode.lc20221210;

import sun.reflect.generics.tree.Tree;

import java.util.ArrayDeque;
import java.util.Queue;

/*
 * @author lzy
 * @version 1.0
 * */
class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode() {
    }

    TreeNode(int val) {
        this.val = val;
    }

    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

public class Solution01 {
    public boolean isSymmetric1(TreeNode root) {
        //思路1： 队列实现
        //边界值判断
        if (root.right == null && root.left == null) {
            return true;
        } else if (root.right != null && root.left != null) {

        } else {
            return false;
        }
        //层序遍历即可
        Queue<TreeNode> q = new ArrayDeque();
        q.offer(root.left);
        q.offer(root.right);
        while (!q.isEmpty()) {
            TreeNode left = q.poll();
            TreeNode right = q.poll();
            if (left.val == right.val) {
                //如果对称节点一个为空另一个不为空，那么肯定不是对称树
                TreeNode leftleft = left.left;
                TreeNode leftright = left.right;
                TreeNode rightright = right.right;
                TreeNode rightleft = right.left;
                if (leftleft == null && rightright == null) {

                } else if (leftleft != null && rightright != null) {
                    q.offer(leftleft);
                    q.offer(rightright);
                } else {
                    return false;
                }
                if (leftright == null && rightleft == null) {

                } else if (leftright != null && rightleft != null) {
                    q.offer(leftright);
                    q.offer(rightleft);
                } else {
                    return false;
                }
            } else {
                //对称的两个节点值应该一致，不一致则返回false；
                return false;
            }
        }
        return true;
    }

    //解法2：递归判断
    //递归退出条件：left right 不等，left right 为null
    //递归主题逻辑：判断left 与 right是否相等，然后递归的调用left和 right
    //递归初试化操作。
    public boolean isSymmetric(TreeNode root) {
        //边界值判断
        return dfs(root.left, root.right);
    }

    private boolean dfs(TreeNode left, TreeNode right) {
        //左右节点都为null
        if (left == null && right == null) {
            return true;
        //左右节点都不为空
        } else if (left != null && right != null) {
            //如果两者相等，那么镜像地判断其孩子节点
            if (left.val == right.val) {
                return dfs(left.left,right.right) && dfs(left.right, right.left);
            } else {
                //如果不同，则返回false
                return false;
            }
        } else {
            //左右节点有一为空 有一不为空
            return false;
        }
    }
}