参考：(3条消息) Dijkstra算法图文详解_一叶执念的博客-CSDN博客_迪杰斯特拉算法

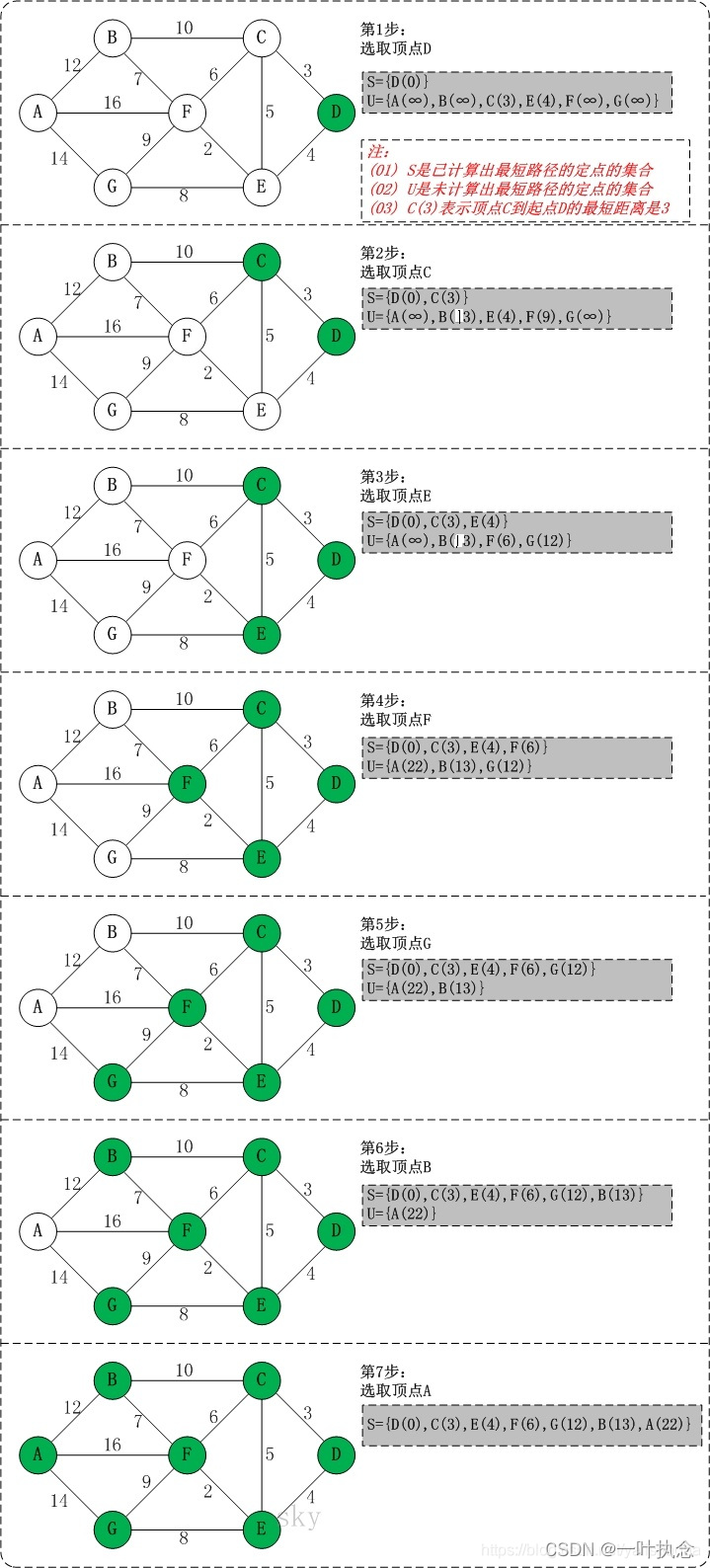
 如图，假设图中共有n条路径（如D-C-E），根据路径长度进行小到大排序。

1、起点到达某终点的距离是无穷符号，表示该起点还需要借助中间某个端点才能到达该终点，所以起点到该终点的距离肯定不是最小，因为起点到该中间端点的距离就小于起点到该终点的距离。

2、一旦确定某端点是当前最小距离端点，除了把该端点加入到S集合中，还需要把紧挨着该端点的邻接点也加入到比较的范围之列，进行下一轮比较，不是该端点邻接点的端点要么需要借助该端点的邻接点才能到达，要么需要借助当前已参与比较的其它端点才能到达，所以肯定不是最短的；另外由于下一轮最短的未必就是当前次最短的，起点到当前最短路径的邻近点的路径可能还小于当前次最短路径。

3、在当前可比较范围之列中，如果有多条到同一终点的路径，先比较这些到同一终点的路径，比出最短路径，其余路径都删除，由该最短路径代表其它删除路径进行参选比较当前最短路径。

4、图中的总共的n条路径由小到大排好序后，那么出现在最前面的到达不同终点的路径就是起点到该终点的最短路径，因为它们排在最前面，所以已经没有哪条到该相同终点的路径比它们更小的了，有也是更大排在了后面。

egg：

假如CE边的权值是2，那么从小到大前几长度依次是：

路径                长度

D--->C               3

D--->E               4

D--->C--->E       5

D--->E--->F       6

........

虽然D->C->E排在D->E->F之前，但是D到F的最短距离还是D->E->F，且D->C->E因为有D->E更短距离，可以删掉。

5、无穷符号即表示距离无穷大，也可以表示当前可能是最短路径的可能性为零。