A - QQ solverA - QQ solver
题目大意
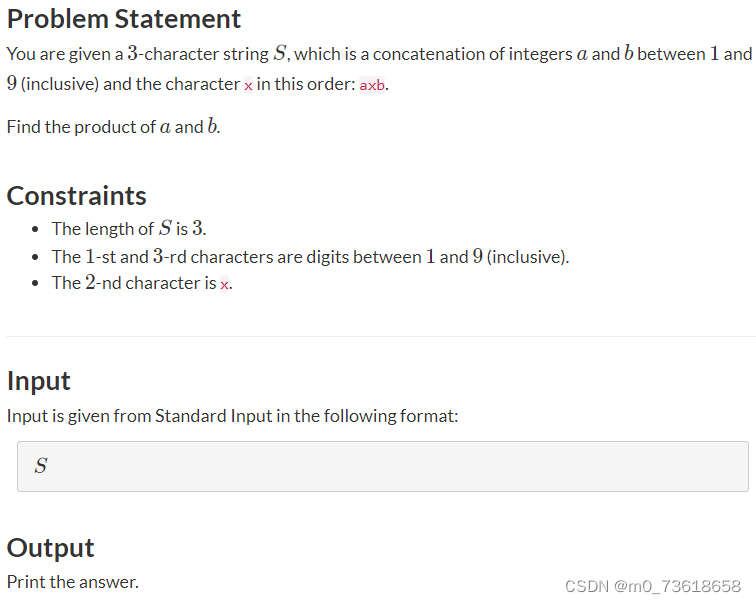
要求从一个长度为3的字符串中提取出两个整数a和b,字符串的格式是axb,其中a和b是介于1到9之间(包括11和99)的整数,计算它们的乘积。
思路分析
将字符类型转换为整数类型来提取出a和b,并计算它们的乘积。
时间复杂度
O(1)
AC代码
#include <iostream>
using namespace std;
int main() {
char a, x, b;
cin >> a >> x >> b;
cout << (int)(a - '0') * (int)(b - '0') << '\n';
}
B - Caesar Cipher B - Caesar Cipher
题目大意
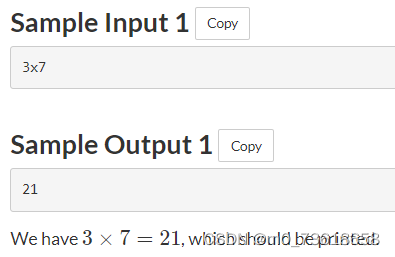
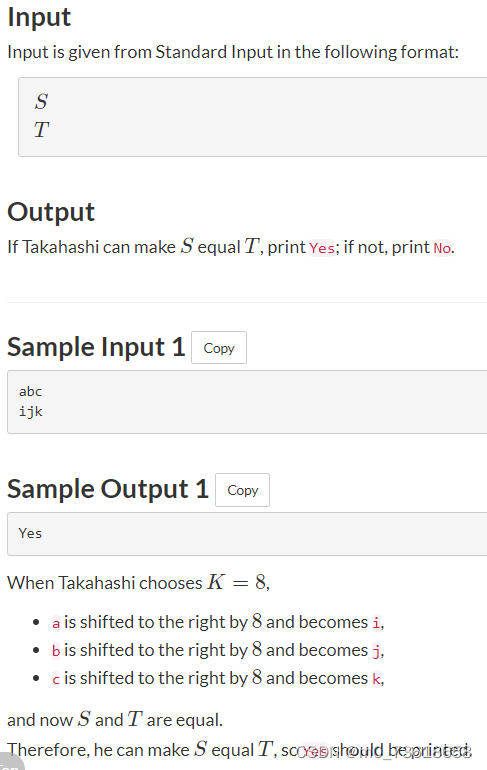
判断是否存在一个非负整数K,使得将字符串S中的每个字符向右移动K位后得到字符串T。
思路分析
- 找到第一个字符对应的K值。根据题目描述,可以通过计算(t[0] - s[0] + 26) % 26来得到K的值。这样做的目的是保证K始终为非负数。
- 然后,遍历字符串S和T的每个字符,如果发现有任何一个字符经过移动后不等于T中对应位置的字符,则输出"No"。否则,当所有字符移动后与T相等时,输出"Yes"。
时间复杂度
O(n)
AC代码
#include <iostream>
using namespace std;
int main() {
string s, t;
cin >> s >> t;
int k = (t[0] - s[0] + 26) % 26;
for (int i = 0; i < (int)s.size(); i++) {
if ((s[i] - t[i] + 26) % 26 != k) {
cout << "No" << endl;
return 0;
}
}
cout << "Yes" << endl;
return 0;
}
C - Graph IsomorphismC - Graph Isomorphism
题目大意
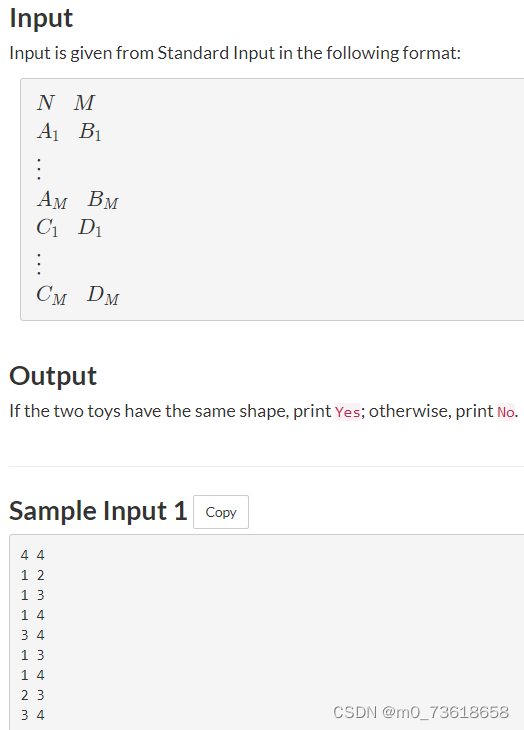
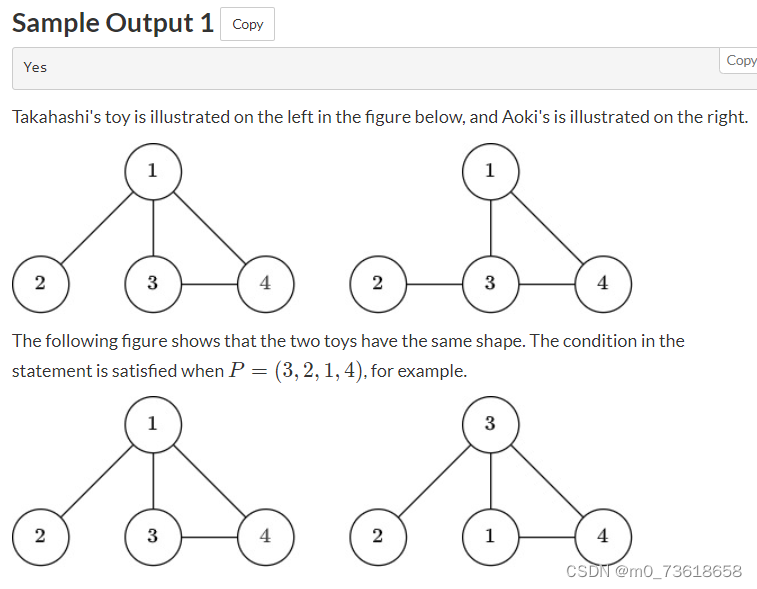
判断两个玩具是否具有相同的形状。每个玩具由N个球和M根绳索组成。在Takahashi的玩具中,球的编号为1到N,第i根绳索连接了球Ai和球Bi。类似地,在Aoki的玩具中,球的编号也为1到N,第i根绳索连接了球Ci和球Di。
思路分析
通过枚举N个球的排列,并验证条件是否满足。具体来说,对于每个排列P,检查Takahashi玩具中球i和球j是否被绳索连接,应该等价于Aoki玩具中球Pi和球Pj是否被绳索连接。如果存在一个排列P使得这个条件对所有i和j都成立,则可以判断两个玩具具有相同的形状。
时间复杂度
O(N^2 * N!)
AC代码
#include <bits/stdc++.h>
using namespace std;
int main() {
int n, m;
cin >> n >> m;
vector<vector<bool>> x(n, vector<bool>(n)), y(n, vector<bool>(n));
// 读取Takahashi玩具的绳索连接关系
for (int i = 0; i < m; ++i) {
int a, b;
cin >> a >> b;
a -= 1, b -= 1;
x[a][b] = x[b][a] = true;
}
// 读取Aoki玩具的绳索连接关系
for (int i = 0; i < m; ++i) {
int c, d;
cin >> c >> d;
c -= 1, d -= 1;
y[c][d] = y[d][c] = true;
}
vector<int> p(n);
iota(begin(p), end(p), 0);
do {
bool ok = true;
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (x[i][j] != y[p[i]][p[j]]) {
ok = false;
}
}
}
if (ok) {
cout << "Yes\n";
return 0;
}
} while (next_permutation(begin(p), end(p)));
cout << "No\n";
}