来一手结论！：贝西想要经过最多的地标数量，一定不能反复横跳

所以简单了：（）

题目问的是最多可以访问多少地标。稍稍分析可知，多访问一个路标，时间必定不会减少，显然这具有单调性质。于是很自然的可以想到去二分路标的个数呀QwQ

先将所有路标的位置排序。要尽量使用时最少，那么我访问的任意两个路标之间都不能有其他的东西。（因为如果我访问的两个路标之间还有路标，那我还不如把这个路标顺便一起访问了呢）

那么，在存储路标位置的数组中，只要排好序，我访问的路标就一定是下标相邻的。

二分能访问到的路标个数，枚举右端点（当然左端点也行），判断这个区间是否能在�t的时间内访问完成。

最后右端点枚举完了，如果还没有找到解，那就证明当前二分的这个路标个数不行。

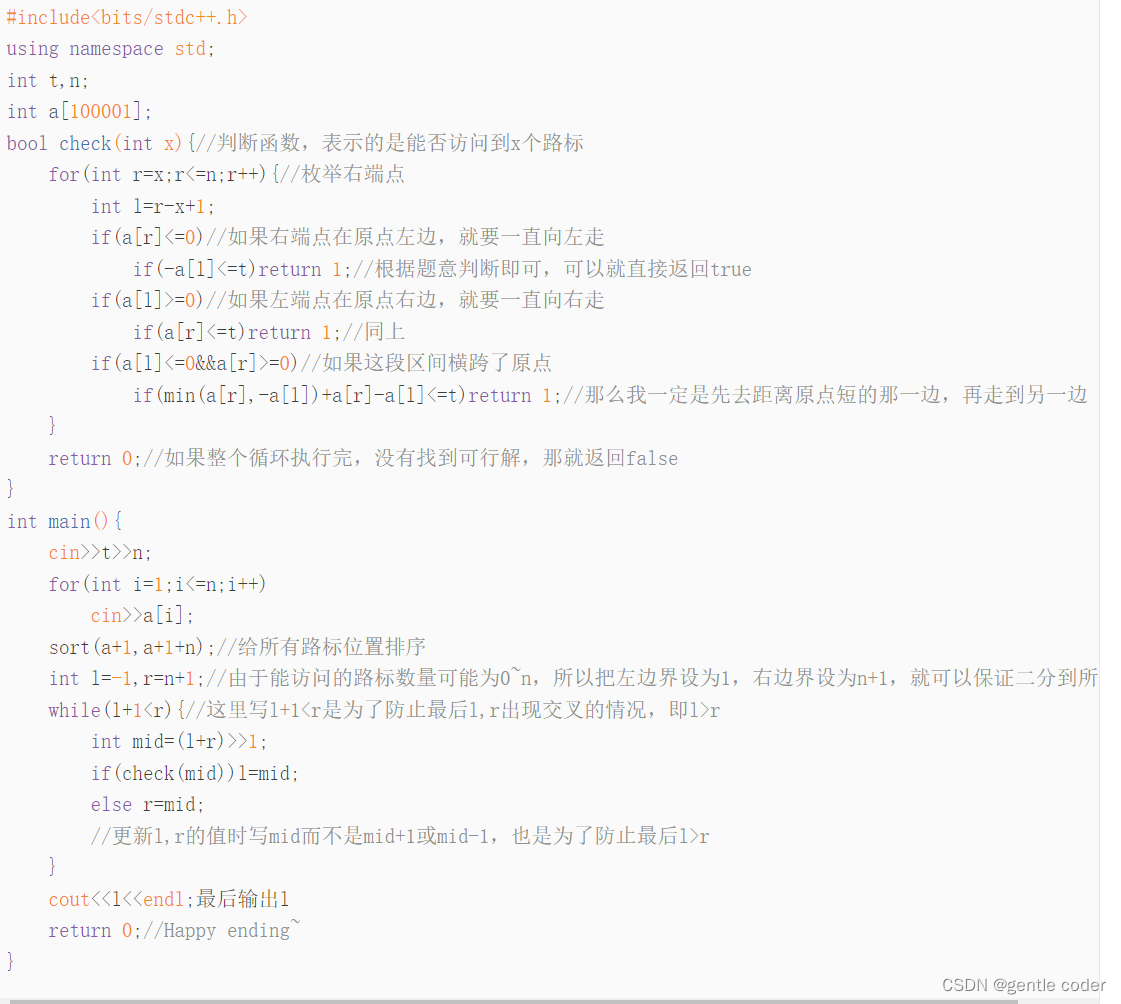
ACcode:(另外配上注释版本)

#include<bits/stdc++.h>
using namespace std;
const int N=5e4+10;
int t,n,a[N];
bool check(int x){
	for(int r=x;r<=n;r++){
		int l=r-x+1;
		if(a[l]>=0){
			if(a[r]<=t) return true;
		} 
		if(a[r]<=0){
			if(-a[l]<=t) return true;
		}
		if(a[l]<=0&&a[r]>=0){
			if(min(-a[l],a[r])+a[r]-a[l]<=t) return true;
		}
	}
	return false;
}
void solve() {
  cin>>t>>n;
  for(int i=1;i<=n;i++) cin>>a[i];
  sort(a+1,a+1+n);
  int l=-1,r=n+1;
  while(l+1<r){
  	int mid=l+r>>1;
  	if(check(mid))l=mid;
  	 else r=mid;
  }
  cout<<l<<"\n";
}
int main() {

	ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
	int tt=1;
//	cin>>tt;
	while(tt--)
		solve();
	return 0;
}

注释版本：

 over~