一、题目一：

53. 最大子数组和

题目要求：

 思路：贪心算法。  求每个区间的和。

• 局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。
• 全局最优：选取最大“连续和”

代码：

class Solution {
    public int maxSubArray(int[] nums) {

        int sum = Integer.MIN_VALUE;
        int count = 0;

        for (int i = 0; i < nums.length; i++) {
            count += nums[i];
            if (sum < count)
// 用 sum记录最大子序与区间和
                sum = count;
            if (count <= 0)
                count = 0; // 相当于重置最大子序起始位置，因为遇到负数一定是拉低总和
        }
        return sum;

    }
}

二、题目二：

56. 合并区间

题目要求：

 思路：先将数组进行排序，然后将左侧数组的右值与右侧数组的左值进行比较，原因是用来判断两个数组之间是否存在重合的部分。

注意：使用idx作为加入到结果数组的子数组个数

代码：

class Solution {
    public int[][] merge(int[][] intervals) {
        // 先按照区间起始位置排序
        Arrays.sort(intervals, (v1, v2) -> v1[0] - v2[0]);
        // 遍历区间
        int[][] res = new int[intervals.length][2];
        int idx = -1;
        for (int[] interval: intervals) {
            // 如果结果数组是空的，或者当前区间的起始位置 > 结果数组中最后区间的终止位置，
            // 则不合并，直接将当前区间加入结果数组。
            if (idx == -1 || interval[0] > res[idx][1]) {
                res[++idx] = interval;
            } else {
                // 反之将当前区间合并至结果数组的最后区间
                res[idx][1] = Math.max(res[idx][1], interval[1]);
            }
        }
        // 将res数组的长度进行规整
        return Arrays.copyOf(res, idx + 1);
    }
}

三、题目三：

189. 轮转数组

题目要求：

 思路：可以参考字符串反转的方法，使用参数t进行交换；也可以直接新建数组进行取余来更新索引；

代码：

class Solution {
    public void rotate(int[] nums, int k) {
        int n = nums.length;
        int[] newArr = new int[n];
        for (int i = 0; i < n; ++i) {
            newArr[(i + k) % n] = nums[i];
        }
        System.arraycopy(newArr, 0, nums, 0, n);
    }
}

四、题目四

238. 除自身以外数组的乘积

题目要求：

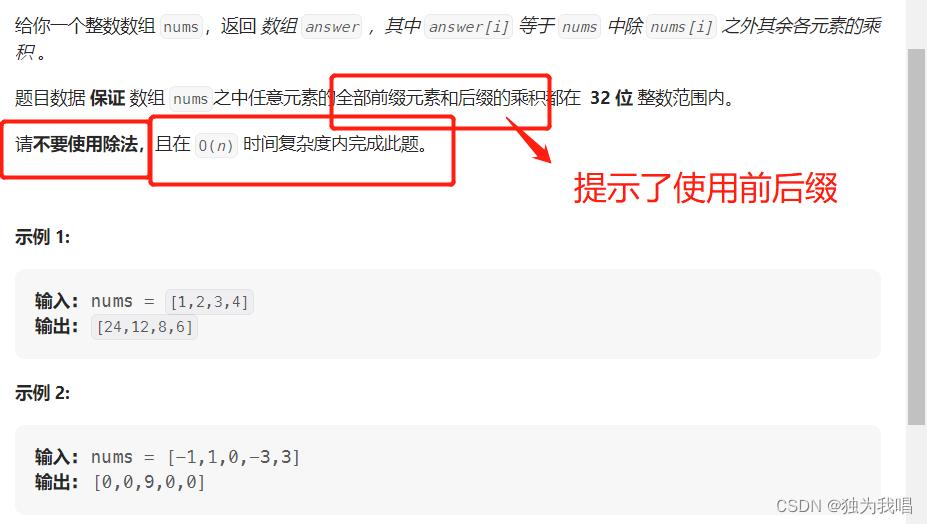
 思路：题目要求不使用除法和时间复杂度O(n)，这里使用前后缀 。即answer[i]的值等于i之前所有数乘积和i之后所有数的乘积，然后再将这两段的结果再进行乘积

过程：前缀之积就是前一个数乘以前一个数的前缀积的相乘，而第一个前缀积默认为1. 

 代码：

class Solution {
    public int[] productExceptSelf(int[] nums) {

        int[] l = new int[nums.length];
        int[] r = new int[nums.length];
        // 前缀
        l[0] = 1;
        for (int i = 1; i < nums.length; i++) {
            l[i] = l[i - 1] * nums[i - 1];
        }
        // 后缀
        r[nums.length - 1] = 1;
        for (int i = nums.length - 2; i >= 0; i--) {
            r[i] = nums[i + 1] * r[i + 1];
        }
        int[] answer = new int[nums.length];

        for (int i = 0; i < nums.length; i++) {
            answer[i] = r[i] * l[i];
        }
        return answer;
    }
}