什么是归并排序法

归并排序是一种常见的排序算法，它基于分治策略，将一个大问题分解为小问题来解决。归并排序的主要思想是将待排序的数组分成两个子数组，分别对这两个子数组进行排序，最后将两个有序的子数组合并成一个有序的数组。

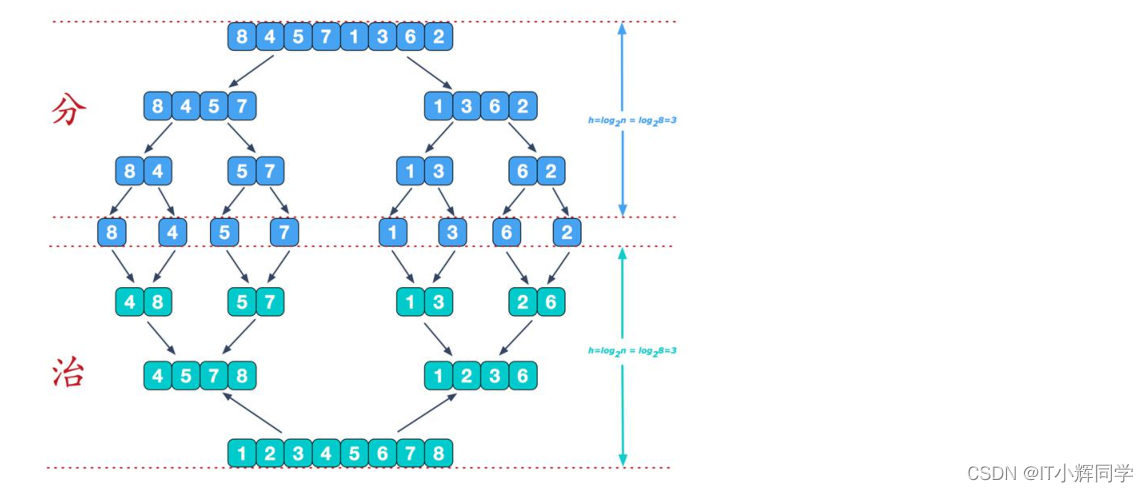
具体步骤如下：

1. 将待排序的数组不断地二分，直到每个子数组只剩下一个元素为止（即子数组长度为1）。
2. 对每个子数组进行排序，可以使用递归来完成。递归结束条件是子数组中只有一个元素，此时认为它已经是有序的。
3. 将两个有序的子数组合并成一个有序的数组。合并过程中，比较两个子数组中的元素，将较小的元素放入新的数组，并将其指针后移一位，直到一个子数组的所有元素都被合并完毕。然后将另一个子数组中剩下的元素直接复制到新的数组中。

归并排序的关键思想是分治和合并。分治将原问题划分成多个子问题，通过递归地解决每个子问题，最终得到解。合并将子问题的解合并成原问题的解。

归并排序的时间复杂度始终为O(nlogn)，其中n是待排序数组的长度。这是因为每次合并操作需要线性的时间复杂度O(n)，而每次递归调用将数组大小减半，所以总共需要logn次递归调用。

归并排序是一种稳定的排序算法，它适用于各种规模的数组排序问题。由于归并排序的稳定性和较低的时间复杂度，它在实际应用中被广泛使用。

代码演示

def merge_sort(arr):
    if len(arr) <= 1:
        return arr

    # 将数组二分为两个子数组
    mid = len(arr) // 2
    left = arr[:mid]
    right = arr[mid:]

    # 递归地对子数组进行排序
    left = merge_sort(left)
    right = merge_sort(right)

    # 合并两个有序子数组
    return merge(left, right)

def merge(left, right):
    merged = []
    i = j = 0

    # 比较两个子数组中的元素，并按顺序合并
    while i < len(left) and j < len(right):
        if left[i] <= right[j]:
            merged.append(left[i])
            i += 1
        else:
            merged.append(right[j])
            j += 1

    # 将剩余的子数组中的元素添加到合并数组中
    merged.extend(left[i:])
    merged.extend(right[j:])

    return merged

# 测试代码
arr = [9, 5, 1, 3, 8, 4, 7, 2, 6]
sorted_arr = merge_sort(arr)
print(sorted_arr)

这段代码通过递归实现了归并排序。首先将数组分为两个子数组，然后递归地对子数组进行排序。最后，调用merge函数将两个有序的子数组合并成一个有序的数组。在merge函数中，我们使用两个指针i和j分别指向左子数组和右子数组，通过比较元素大小来确定合并的顺序。最后，将剩余的元素添加到合并数组中，返回最终的有序数组。

运行上述代码，输出结果为：[1, 2, 3, 4, 5, 6, 7, 8, 9]，即为按照升序排列的原始数组。这就是归并排序的算法思想和实现过程。