文章目录
- 1. 平移 (Translation)
- 2. 缩放 (Scaling)
- 3. 旋转 (Rotation)
- 4. 错切 (Shearing)
- 5. 镜像 (Reflection)
1. 平移 (Translation)
在2D空间中,我们经常需要将一个点平移到另一个位置。假设空间中的一点
P
(
x
,
y
)
P(x,y)
P(x,y);将其向
x
,
y
x, y
x,y方向分别平移
t
x
t_x
tx,
t
y
t_y
ty, 假设平移后点的坐标为
(
x
′
,
y
′
)
(x',y')
(x′,y′),则上述点的平移操作可以归纳为如下公式:
x
′
=
x
+
t
x
y
′
=
x
+
t
y
\begin{alignat}{2} &x'=x + t_x\\ &y'=x + t_y \end{alignat}
x′=x+txy′=x+ty
使用齐次矩阵表示如下:
[
x
′
y
′
1
]
=
[
1
b
t
x
0
1
t
y
0
0
1
]
[
x
y
1
]
\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & b & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
x′y′1
=
100b10txty1
xy1
import numpy as np
def translation():
"""
原始数组a 三个点(1,1) (4,4) (7,7)
构建齐次矩阵 P
构建变换矩阵 T
"""
a = np.array([[1, 1],
[4, 4],
[7, 7]])
P = np.array([a[:, 0],
a[:, 1],
np.ones(len(a))])
T = np.array([[1, 0, 2],
[0, 1, 2],
[0, 0, 1]])
return np.dot(T, P)
print(translation())
"""
[[3. 6. 9.]
[3. 6. 9.]
[1. 1. 1.]]
"""
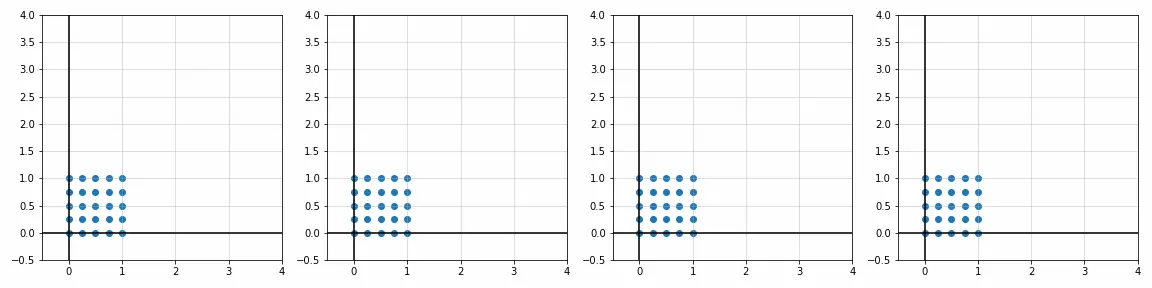
动画效果演示
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
X, Y = np.mgrid[0:1:5j, 0:1:5j]
x, y = X.ravel(), Y.ravel()
def trans_translate(x, y, tx, ty):
T = [[1, 0, tx],
[0, 1, ty],
[0, 0, 1]]
T = np.array(T)
P = np.array([x, y, [1] * x.size])
return np.dot(T, P)
fig, ax = plt.subplots(1, 4)
T_ = [[0, 0], [2.3, 0], [0, 1.7], [2, 2]]
for i in range(4):
tx, ty = T_[i]
x_, y_, _ = trans_translate(x, y, tx, ty)
ax[i].scatter(x_, y_)
ax[i].set_title(r'$t_x={0:.2f}$ , $t_y={1:.2f}$'.format(tx, ty))
ax[i].set_xlim([-0.5, 4])
ax[i].set_ylim([-0.5, 4])
ax[i].grid(alpha=0.5)
ax[i].axhline(y=0, color='k')
ax[i].axvline(x=0, color='k')
plt.show()
2. 缩放 (Scaling)
在2D空间中,点
(
x
,
y
)
(x,y)
(x,y)相对于另一点
(
p
x
,
p
y
)
(p_x,p_y)
(px,py)进行缩放操作,我们不妨缩放因子在
x
,
y
x,y
x,y方向分别为:
s
x
,
s
y
s_x, s_y
sx,sy, 则上述的缩放操作可以归纳为如下公式:
x
′
=
s
x
(
x
−
p
x
)
+
p
x
=
s
x
x
+
p
x
(
1
−
s
x
)
y
′
=
s
y
(
y
−
p
y
)
+
p
y
=
s
y
y
+
p
y
(
1
−
s
y
)
\begin{alignat}{2} &x'=s_x(x-p_x) + p_x &=s_xx + p_x(1-s_x)\\ &y'=s_y(y-p_y) + p_y &=s_yy + p_y(1-s_y) \end{alignat}
x′=sx(x−px)+pxy′=sy(y−py)+py=sxx+px(1−sx)=syy+py(1−sy)
使用齐次矩阵表示如下:
[
x
′
y
′
1
]
=
[
s
x
0
p
x
(
1
−
s
x
)
0
s
y
p
y
(
1
−
s
y
)
0
0
1
]
[
x
y
1
]
\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} s_x& 0 & p_x(1-s_x) \\ 0 & s_y& p_y(1-s_y)\\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
x′y′1
=
sx000sy0px(1−sx)py(1−sy)1
xy1
def trans_scale(x, y, px, py, sx, sy):
T = [[sx, 0 , px*(1 - sx)],
[0 , sy, py*(1 - sy)],
[0 , 0 , 1 ]]
T = np.array(T)
P = np.array([x, y, [1]*x.size])
return np.dot(T, P)
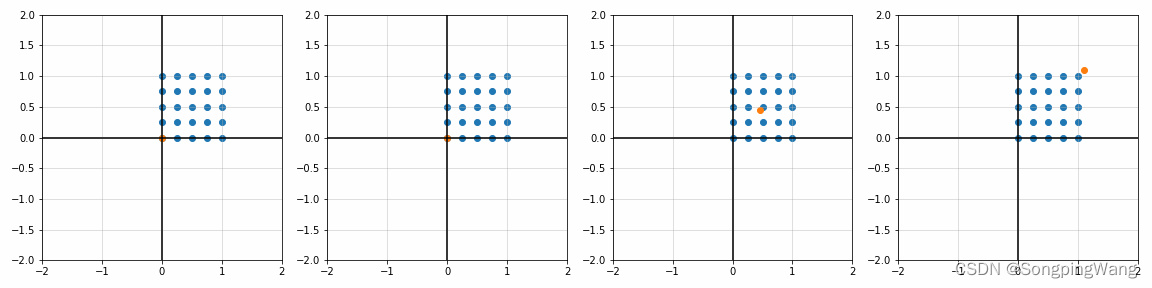
fig, ax = plt.subplots(1, 4)
S_ = [[1, 1], [1.8, 1], [1, 1.7], [2, 2]]
P_ = [[0, 0], [0, 0], [0.45, 0.45], [1.1, 1.1]]
for i in range(4):
sx, sy = S_[i]; px, py = P_[i]
x_, y_, _ = trans_scale(x, y, px, py, sx, sy)
ax[i].scatter(x_, y_)
ax[i].scatter(px, py)
ax[i].set_title(r'$p_x={0:.2f}$ , $p_y={1:.2f}$'.format(px, py) + '\n'
r'$s_x={0:.2f}$ , $s_y={1:.2f}$'.format(sx, sy))
ax[i].set_xlim([-2, 2])
ax[i].set_ylim([-2, 2])
ax[i].grid(alpha=0.5)
ax[i].axhline(y=0, color='k')
ax[i].axvline(x=0, color='k')
plt.show()
3. 旋转 (Rotation)
在2D空间中,对点
(
x
,
y
)
(x,y)
(x,y)相对于另一点
(
p
x
,
p
y
)
(p_x,p_y)
(px,py)进行旋转操作,一般来说逆时针为正,顺时针为负,假设旋转角度为
β
\beta
β, 则上述点
x
,
y
x,y
x,y 相对于点
p
x
,
p
y
p_x,p_y
px,py的旋转角度
β
\beta
β 的操作使用齐次矩阵表示如下:
[
x
′
y
′
1
]
=
[
cos
β
−
sin
β
p
x
(
1
−
cos
β
)
+
p
y
sin
β
sin
β
cos
β
p
y
(
1
−
cos
β
)
+
p
x
sin
β
0
0
1
]
[
x
y
1
]
\begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \beta& -\sin \beta & p_x(1-\cos \beta) + p_y \sin \beta \\ \sin \beta & \cos \beta& p_y(1-\cos \beta) + p_x \sin \beta \\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
x′y′1
=
cosβsinβ0−sinβcosβ0px(1−cosβ)+pysinβpy(1−cosβ)+pxsinβ1
xy1
def trans_rotate(x, y, px, py, beta):
beta = np.deg2rad(beta)
T = [[np.cos(beta), -np.sin(beta), px*(1 - np.cos(beta)) + py*np.sin(beta)],
[np.sin(beta), np.cos(beta), py*(1 - np.cos(beta)) - px*np.sin(beta)],
[0 , 0 , 1 ]]
T = np.array(T)
P = np.array([x, y, [1]*x.size])
return np.dot(T, P)
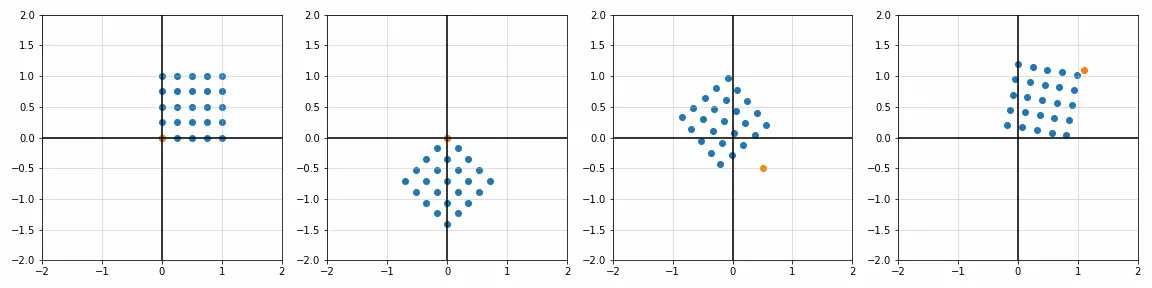
fig, ax = plt.subplots(1, 4)
R_ = [0, 225, 40, -10]
P_ = [[0, 0], [0, 0], [0.5, -0.5], [1.1, 1.1]]
for i in range(4):
beta = R_[i]; px, py = P_[i]
x_, y_, _ = trans_rotate(x, y, px, py, beta)
ax[i].scatter(x_, y_)
ax[i].scatter(px, py)
ax[i].set_title(r'$\beta={0}°$ , $p_x={1:.2f}$ , $p_y={2:.2f}$'.format(beta, px, py))
ax[i].set_xlim([-2, 2])
ax[i].set_ylim([-2, 2])
ax[i].grid(alpha=0.5)
ax[i].axhline(y=0, color='k')
ax[i].axvline(x=0, color='k')
plt.show()
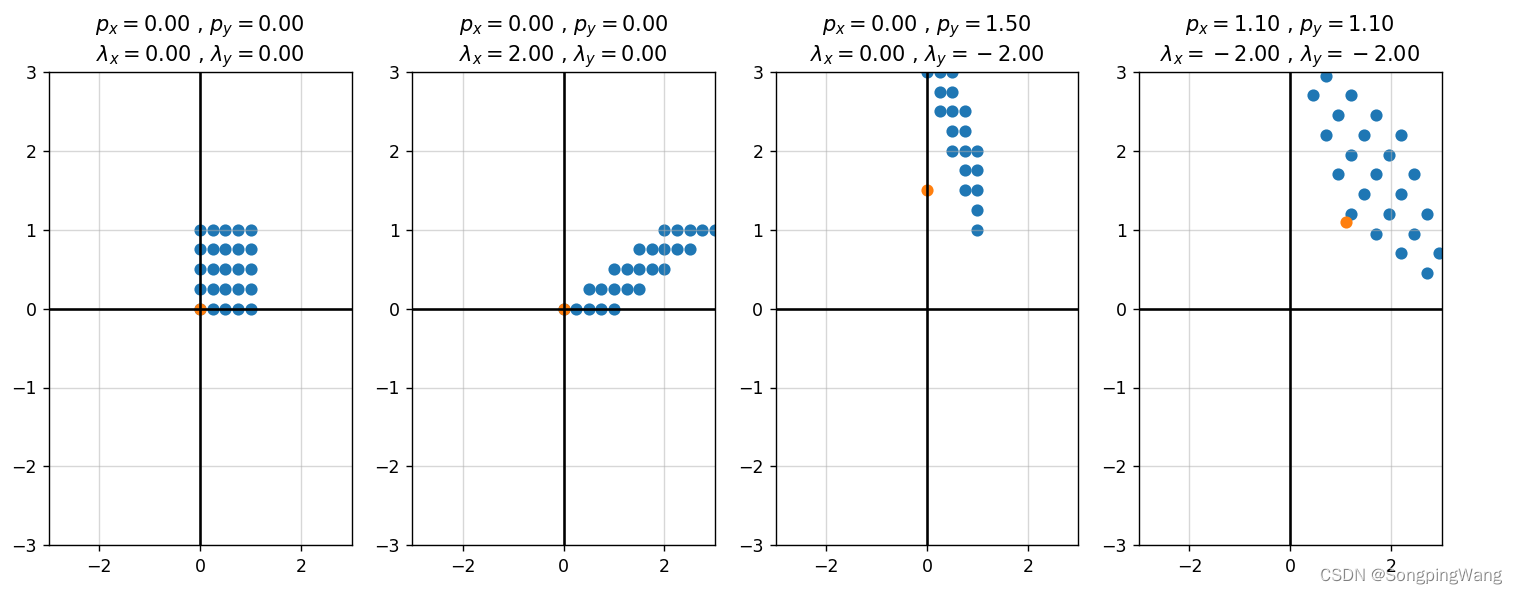
4. 错切 (Shearing)
在2D空间中,对点 ( x , y ) (x,y) (x,y) 相对于另一点 ( p x , p y ) (p_x,p_y) (px,py)进行错切操作,错切一般用于弹性物体的变形处理。 假设沿x 方向与y方向错切参数分别为 λ x , λ y \lambda _x,\lambda _y λx,λy, 则的错切操作可以归纳使用齐次矩阵表示如下:
[ x ′ y ′ 1 ] = [ 1 λ x − λ x p x λ y 1 − λ y p y 0 0 1 ] [ x y 1 ] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} 1& \lambda _x & -\lambda _x p_x \\ \lambda _y & 1& -\lambda _y p_y \\ 0 & 0& 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} x′y′1 = 1λy0λx10−λxpx−λypy1 xy1
import matplotlib.pyplot as plt
import numpy as np
X, Y = np.mgrid[0:1:5j, 0:1:5j]
x, y = X.ravel(), Y.ravel()
def trans_shear(x, y, px, py, lambdax, lambday):
T = [[1 , lambdax, -lambdax*px],
[lambday, 1 , -lambday*py],
[0 , 0 , 1 ]]
T = np.array(T)
P = np.array([x, y, [1]*x.size])
return np.dot(T, P)
fig, ax = plt.subplots(1, 4)
L_ = [[0, 0], [2, 0], [0, -2], [-2, -2]]
P_ = [[0, 0], [0, 0], [0, 1.5], [1.1, 1.1]]
for i in range(4):
lambdax, lambday = L_[i]; px, py = P_[i]
x_, y_, _ = trans_shear(x, y, px, py, lambdax, lambday)
ax[i].scatter(x_, y_)
ax[i].scatter(px, py)
ax[i].set_title(r'$p_x={0:.2f}$ , $p_y={1:.2f}$'.format(px, py) + '\n'
r'$\lambda_x={0:.2f}$ , $\lambda_y={1:.2f}$'.format(lambdax, lambday))
ax[i].set_xlim([-3, 3])
ax[i].set_ylim([-3, 3])
ax[i].grid(alpha=0.5)
ax[i].axhline(y=0, color='k')
ax[i].axvline(x=0, color='k')
plt.show()
5. 镜像 (Reflection)
对于镜像,对称轴的法向量
v
(
v
x
,
v
y
)
v(v_x,v_y)
v(vx,vy), 镜像矩阵
T
m
T_{m}
Tm表示为:
[
1
−
2
x
v
2
−
2
x
v
y
v
0
−
2
x
v
y
v
1
−
2
y
v
2
0
0
0
1
]
\left[ \begin{array}{ccc} 1-2 x_{v}{ }^{2} & -2 x_{v} y_{v} & 0 \\ -2 x_{v} y_{v} & 1-2 y_{v}{ }^{2} & 0 \\ 0 & 0 & 1 \end{array} \right]
1−2xv2−2xvyv0−2xvyv1−2yv20001
另外就是需要一个表示对称轴位置的点(对称轴2点中任意一点),表示为
M
(
x
m
,
y
m
)
M\left(x_{\mathrm{m}}, y_{m}\right)
M(xm,ym),变换矩阵
H
=
T
t
∗
T
m
∗
T
t
−
1
H = T_{t}*T_{m}*T_{t}^{-1}
H=Tt∗Tm∗Tt−1,即:
H
=
[
1
0
0
0
1
0
x
m
y
m
1
]
[
1
−
2
x
v
2
−
2
x
v
y
v
0
−
2
x
v
y
v
1
−
2
y
v
2
0
0
0
1
]
[
1
0
0
0
1
0
−
x
m
−
y
m
1
]
H = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ x_{\mathrm{m}} & y_{m} & 1 \end{array} \right] \left[ \begin{array}{ccc} 1-2 x_{v}{ }^{2} & -2 x_{v} y_{v} & 0 \\ -2 x_{v} y_{v} & 1-2 y_{v}{ }^{2} & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -x_{\mathrm{m}} & -y_{m} & 1 \end{array} \right]
H=
10xm01ym001
1−2xv2−2xvyv0−2xvyv1−2yv20001
10−xm01−ym001
镜像后的坐标即为
T
o
∗
T
t
∗
T
m
∗
T
t
−
1
T_{o}*T_{t}*T_{m}*T_{t}^{-1}
To∗Tt∗Tm∗Tt−1。
沿 X 轴 镜像的镜像矩阵:
[
1
0
0
0
−
1
0
1
0
1
]
\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 1 & 0 & 1 \end{array} \right]
1010−10001
沿 Y 轴 镜像的镜像矩阵:
[
−
1
0
0
0
1
0
0
1
1
]
\left[ \begin{array}{ccc} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 1 & 1 \end{array} \right]
−100011001
import numpy as np
a = np.array([[1, 2],
[2, 2],
[3, 5],
[4, 6]])
a = np.array([a[:,0], a[:,1], np.ones(len(a))])
print("\n",a)
print("--------------------------------")
T_x = np.array( [[ 1, 0, 0],
[ 0, -1, 0],
[ 1, 0, 1]])
print("\n",np.dot(T_x, a))
print("=================================")
T_y = np.array( [[-1, 0, 0],
[ 0, 1, 0],
[ 0, 1, 1]])
print("\n",np.dot(T_y, a))
参考:
https://zhuanlan.zhihu.com/p/387578291
https://zhuanlan.zhihu.com/p/187411029
https://blog.csdn.net/Akiyama_sou/article/details/122144415






![[PyTorch][chapter 44][RNN]](https://img-blog.csdnimg.cn/5c9ce532a7874142a72ff4c348583dc2.png)