因果推断（一）合成控制法（SCM）

在互联网时代，产品迭代速度越来越快，营销活动也越来越多。分析师因此需要快速的量化每次迭代或每次营销的效果，探索改变与结果之间的因果关系，并将优秀的改变用以引导迭代方向，指导业务朝正确方向行走。

但产品本身具有明显的时间趋势，例如季节性、周期性，亦或自然增长趋势，而且营销活动本身也带有较强的噪音。因此如何排除这些干扰因素来量化真正的影响就显得尤为重要了。

在互联网中最常见的自然就是A/B试验，但现实情况中有很多情况下无法开展实验，这个时候就只能观察业务历史数据了。好在统计学上有一些经典的因果推断方法，例如合成控制法、倾向匹配得分等。

总结我们前面的一些专题分析，发现基本都是总结各因素与标的变量的相关性，即如果数据存在某些特征，则很大概率出现某种结果。但是我们无法断定如果数据存在某些特征，则一定出现某种结果。这就是相关性与因果性的差异。

因果推断是一门复杂的学科，但本质是反事实推断，即在假设没有发生的情况下，如果采取某种干预，会发生什么结果。如果又想深入研究的同学可以参考Causal Inference for The Brave and True

使用背景

德国统一是否影响了西德经济呢？那常见的思路就是比较没有统一的西德和统一的西德在同一时间上的经济差异，此时没有统一的西德就是反事实了，我们可以合成一个假的西德，这样在同一时间就同时出现了统一的西德和统一的西德，该方法就是合成控制法，本文参考自How to use SyntheticControlMethods。

合成控制法的核心就是构造一个相似的对照组，原理简单且具有说服力，因此对业务很友好。例如广告在北京投放一段时间后，用户增长了30%，是否可以直接推广到全国呢？怎么判断这个提升不是来自于自然增长呢？所以利用其余城市合成一个北京，就可以进行简单的比较了，

⚠️注意：合成控制法常用于面板数据

Python实战

数据准备

# pip install SyntheticControlMethods

import pandas as pd
import numpy as np
from scipy.optimize import fmin_slsqp, minimize
from matplotlib import pyplot as plt
from SyntheticControlMethods import Synth, DiffSynth

以下数据如果有需要的同学可关注公众号HsuHeinrich，回复【因果推断01】自动获取～

# 数据查看
data = pd.read_csv("german_reunification.csv")
data = data.drop(columns="code", axis=1) # 删除多余的id列
data.head()

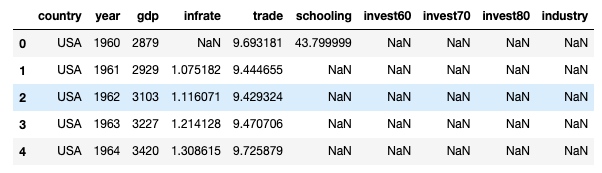
• 数据格式要求
  • 数值变量，id变量可以是分类变量
  • 存在唯一id变量，如果有多个，删除一个。例如本例删除code，保留country
  • 数据按照id列和time列排序
  • 数据集必须包含一个控制组和多个对照组。较多的对照组合成误差更小
  • 结果变量非空，协变量可以含有空值
• Synth主要参数
  • data：数据集
  • outcome_var：结果变量，eg:gdp
  • id_var: ID变量，eg：country
  • time_var：时间变量，eg：year
  • treatment_period：干预时期，eg：1990-德国统一日期
  • treated_unit：干预组，eg：West Germany

模型拟合

# 合成控制拟合
sc = Synth(data, "gdp", "country", "year", 1990, "West Germany", n_optim=100) # 1990-德国统一日期

结果展示

# 查看合成结果
print(sc.original_data.weight_df)
print('-'*60)
print(sc.original_data.comparison_df)
print('-'*60)
print(sc.original_data.rmspe_df)

           Weight
USA      0.396718
Belgium  0.603282
------------------------------------------------------------
           West Germany  Synthetic West Germany    WMAPE  Importance
gdp             8169.83                 8148.46  1002.35        0.13
infrate            3.39                    5.08     1.69        0.12
trade             45.76                   71.27    50.07        0.13
schooling         55.78                   37.48    18.31        0.13
invest60           0.34                    0.26     0.08        0.12
invest70           0.33                    0.27     0.06        0.12
invest80          27.02                   22.07     4.94        0.12
industry          39.69                   35.30     4.39        0.12
------------------------------------------------------------
           unit  pre_rmspe   post_rmspe   post/pre
0  West Germany  96.243293  2246.032119  23.337025

• weight：合成的主要权重为USA和Belgium
• comparison：与西德相比，合成控制的结果
• rmspe：与西德相比，合成控制结果的均方根预测误差96.24，较低

# 观察实验结果
sc.plot(["original", "pointwise", "cumulative"], treated_label="West Germany", 
            synth_label="Synthetic West Germany", treatment_label="German Reunification")

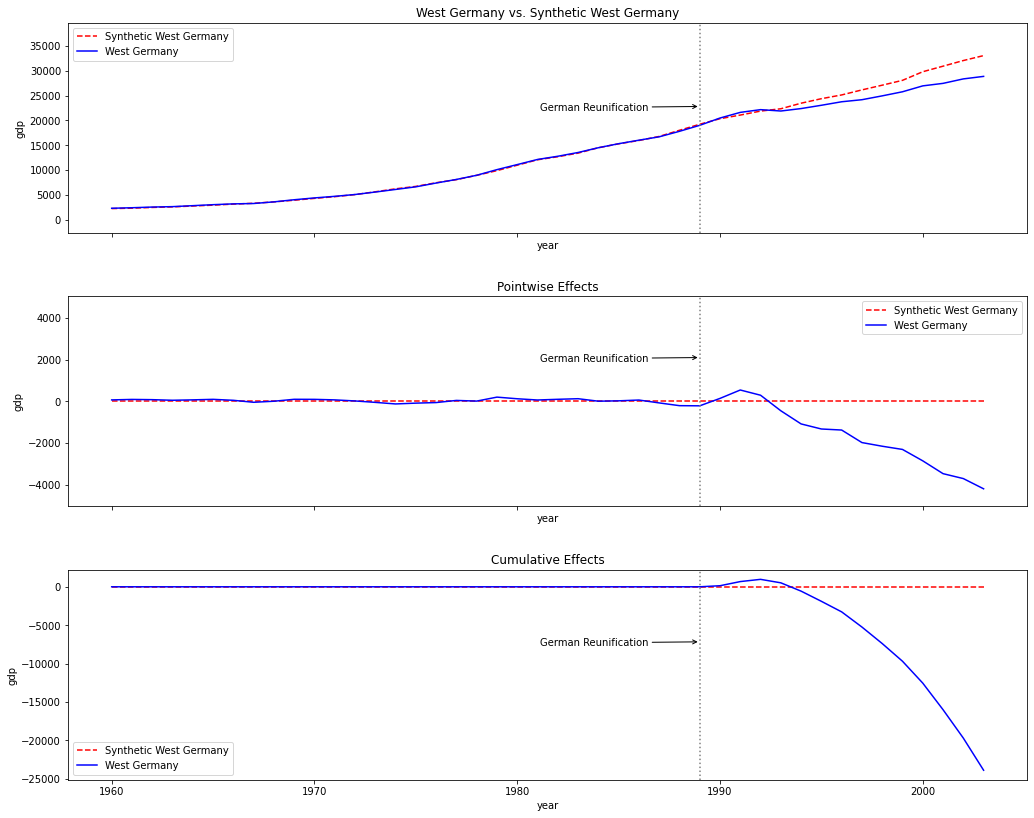
• 可以看出西德与合成控制结果的反事实干预下的趋势基本一致
• 在干预后，实际西德较对照组（合成控制结果）经济明显下滑，第三张图为累计效应，即经济累计下滑显著

模型评估

# 模型评估
# 加入时间安慰剂
sc.in_time_placebo(1982, n_optim=10) # 将干预时间变更为1982念
sc.plot(['in-time placebo'], 
            treated_label="West Germany",
            synth_label="Synthetic West Germany")

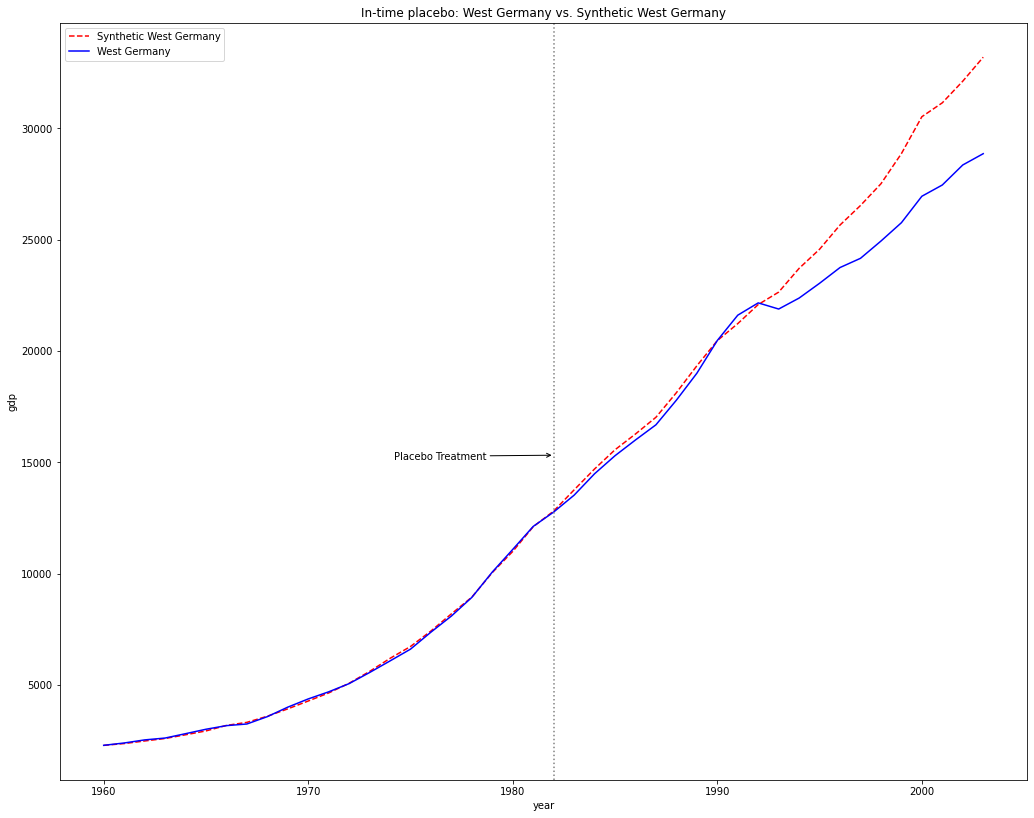
直到1990真实的干预时期，西德与对照组的差异基本一致，没有明显扩大差异。因此合成效果较好

# 加入空间安慰剂
sc.in_space_placebo(10)
sc.plot(['rmspe ratio'])

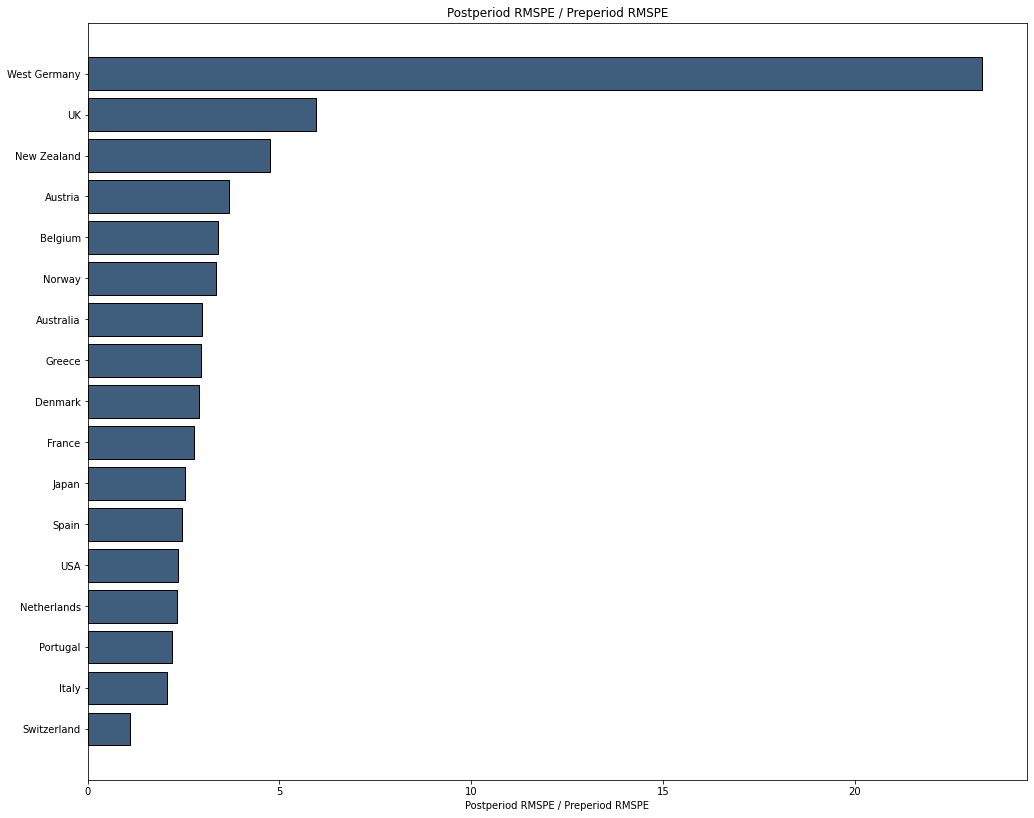
循环地对每个组、其余组合成进行干预，可以发现西德在干预前后的RMSPE差异最大。因此合成效果较好

总结

合成控制法能很好的解决构造相似的对照组，然后在同一干预下，就能很好的比较实验与对照组的差异了。

共勉～