论文笔记--Distilling the Knowledge in a Neural Network
- 1. 文章简介
- 2. 文章概括
- 3 文章重点技术
- 3.1 Soft Target
- 3.2 蒸馏Distillation
- 4. 文章亮点
- 5. 原文传送门
1. 文章简介
- 标题:Distilling the Knowledge in a Neural Network
- 作者:Hinton, Geoffrey, Oriol Vinyals, Jeff Dean
- 日期:2015
- 期刊:arxiv
2. 文章概括
文章提出了一种将大模型压缩的新的思路:蒸馏distillation。通过蒸馏,可以将很大的模型压缩为轻量级的模型,从而提升推理阶段的速率。
3 文章重点技术
3.1 Soft Target
随着模型的参数量越来越大,如何从训练好的大模型(教师模型)学习一个轻量级的小模型(学生模型)是一个重要课题。传统的hard-target训练直接学习大模型的预测结果,无法学习到不正确的类别之间的相对关系。比如给定一张宝马的照片,假设教师模型给出的预测结果为宝马,学生模型只从教师模型中学习到“宝马”这一个标签信息。事实上,教师模型还会给出其它类别的信息,比如将宝马预测为垃圾车为0.02,将宝马预测为胡萝卜的概率仅为0.0001,但学生模型没有学习到垃圾车和胡萝卜之间的区别。
我们需要一种方法来使得学生学习到正确的标签,以及错误标签的相对关系。文章提出“soft-target",即通过学习教师模型的预测概率分布来训练小模型。
3.2 蒸馏Distillation
对一个分类模型,假设教师模型的输出层给出的logits为
z
i
z_i
zi,然后通过计算Softmax得到预测概率:
q
i
=
exp
(
z
i
/
T
)
∑
j
exp
(
z
j
/
T
)
q_i = \frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)}
qi=∑jexp(zj/T)exp(zi/T),其中相比于传统的SoftMax增加了
T
T
T表示温度,用于控制输出概率分布的平滑度。
T
T
T越大,不同类别之间的差异越不明显,即分布越平滑。可以参考
e
x
p
exp
exp的函数曲线来理解:给定
x
1
,
x
2
x_1, x_2
x1,x2,由当
T
T
T越大时,
x
1
/
T
,
x
2
/
T
x_1/T, x_2/T
x1/T,x2/T对应的导数越小(导数即为
exp
(
x
)
\exp(x)
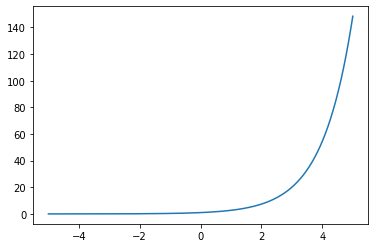
exp(x),也可参考下图),从而差距越小,分布越平滑。当
T
=
1
T=1
T=1时,即传统的Softmax。
我们希望学生模型满足:1) 模型可以学习到教师模型的预测概率,即soft targets; 2)学生模型可以预测真实的标签。从而我们可以考虑2个目标函数:
L
hard
\mathcal{L}_{\text{hard}}
Lhard和
L
soft
\mathcal{L}_{\text{soft}}
Lsoft。首先我们记学生模型和教师模型的logits分别为
z
i
,
v
i
z_i, v_i
zi,vi,预测概率分别为
q
i
,
p
i
q_i, p_i
qi,pi,真实标签为labels,则
- L hard = Cross Entropy ( labels , arg max i ( exp ( z i / T ) ∑ j exp ( z j / T ) ) ) \mathcal{L}_{\text{hard}}=\text{Cross Entropy}\left(\text{labels}, \argmax_i \left(\frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)}\right)\right) Lhard=Cross Entropy(labels,argmaxi(∑jexp(zj/T)exp(zi/T)))
-
L
soft
=
Cross Entropy
(
p
,
q
)
=
Cross Entropy
(
(
exp
(
v
i
/
T
)
∑
j
exp
(
v
j
/
T
)
)
,
(
exp
(
z
i
/
T
)
∑
j
exp
(
z
j
/
T
)
)
)
\mathcal{L}_{\text{soft}}=\text{Cross Entropy}\left(p, q \right) =\text{Cross Entropy}\left((\frac {\exp (v_i/T)}{\sum_j \exp (v_j/T)}), (\frac {\exp (z_i/T)}{\sum_j \exp (z_j/T)})\right)
Lsoft=Cross Entropy(p,q)=Cross Entropy((∑jexp(vj/T)exp(vi/T)),(∑jexp(zj/T)exp(zi/T)))
考虑 L soft \mathcal{L}_{\text{soft}} Lsoft的梯度 ∂ L soft ∂ z k = ∂ ( − ∑ i p i log q i ) ∂ z k = − ∑ i p i q i ∂ q i ∂ z k = − p k q k ∂ q k ∂ z k − ∑ i ≠ k p i q i ∂ q i ∂ z k = − 1 T p k q k q k ( 1 − q k ) + ∑ i ≠ k p i q i exp ( z i / T ) ( ∑ j exp ( z j / T ) ) 2 1 T exp ( z k / T ) = 1 T ( − p k ( 1 − q k ) + ∑ i ≠ k p i q i q i q k ) = 1 T ( − p k + ∑ i p i q k ) = 1 T ( q k − p k ) = 1 T ( exp ( z k / T ) ∑ j exp ( z j / T ) − exp ( v k / T ) ∑ j exp ( v j / T ) ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} = \frac {\partial (-\sum_i p_i \log q_i)}{\partial z_k} = -\sum_i \frac {p_i}{q_i} \frac{\partial q_i}{\partial z_k} = -\frac {p_k}{q_k} \frac{\partial q_k}{\partial z_k}-\sum_{i\neq k} \frac {p_i}{q_i} \frac{\partial q_i}{\partial z_k} \\=-\frac 1T \frac {p_k}{q_k} q_k (1-q_k) +\sum_{i\neq k} \frac {p_i}{q_i} \frac {\exp (z_i/T)}{(\sum_j \exp (z_j/T))^2} \frac 1T \exp (z_k/T) \\= \frac 1T (-p_k (1-q_k) + \sum_{i\neq k} \frac {p_i}{q_i} q_i q_k )= \frac 1T (-p_k + \sum_i p_i q_k ) \\= \frac 1T (q_k - p_k) = \frac 1T \left(\frac {\exp (z_k/T)}{\sum_j \exp (z_j/T)} - \frac {\exp (v_k/T)}{\sum_j \exp (v_j/T)}\right) ∂zk∂Lsoft=∂zk∂(−∑ipilogqi)=−i∑qipi∂zk∂qi=−qkpk∂zk∂qk−i=k∑qipi∂zk∂qi=−T1qkpkqk(1−qk)+i=k∑qipi(∑jexp(zj/T))2exp(zi/T)T1exp(zk/T)=T1(−pk(1−qk)+i=k∑qipiqiqk)=T1(−pk+i∑piqk)=T1(qk−pk)=T1(∑jexp(zj/T)exp(zk/T)−∑jexp(vj/T)exp(vk/T)),当 T T T相比于 z i , v i z_i, v_i zi,vi等logits量级比较高时,有 z i / T → 0 , v i / T → 0 z_i/T\to 0, v_i/T \to 0 zi/T→0,vi/T→0,从而由泰勒公式上式近似为 ∂ L soft ∂ z k ≈ 1 T ( 1 + z k / T N + ∑ j z j / T − 1 + v k / T N + ∑ j v j / T ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} \approx \frac 1T \left(\frac {1+z_k/T}{N + \sum_j z_j/T} - \frac {1+v_k/T}{N + \sum_j v_j/T}\right) ∂zk∂Lsoft≈T1(N+∑jzj/T1+zk/T−N+∑jvj/T1+vk/T),假设logits都是零均值的,则有 ∂ L soft ∂ z k ≈ 1 N T 2 ( z k − v k ) \frac {\partial \mathcal{L}_{\text{soft}}}{\partial z_k} \approx \frac 1{NT^2} (z_k - v_k) ∂zk∂Lsoft≈NT21(zk−vk)。从而当温度比较高时,我们的目标近似为最小化 1 2 ( z k − v k ) 2 \frac 12 (z_k - v_k)^2 21(zk−vk)2(上式的原函数,不考虑常数项),即最小化logits的MSE函数。温度越低,我们越关注小于均值的logits。
最终的损失函数为上述hard和soft损失的加权求和。
4. 文章亮点
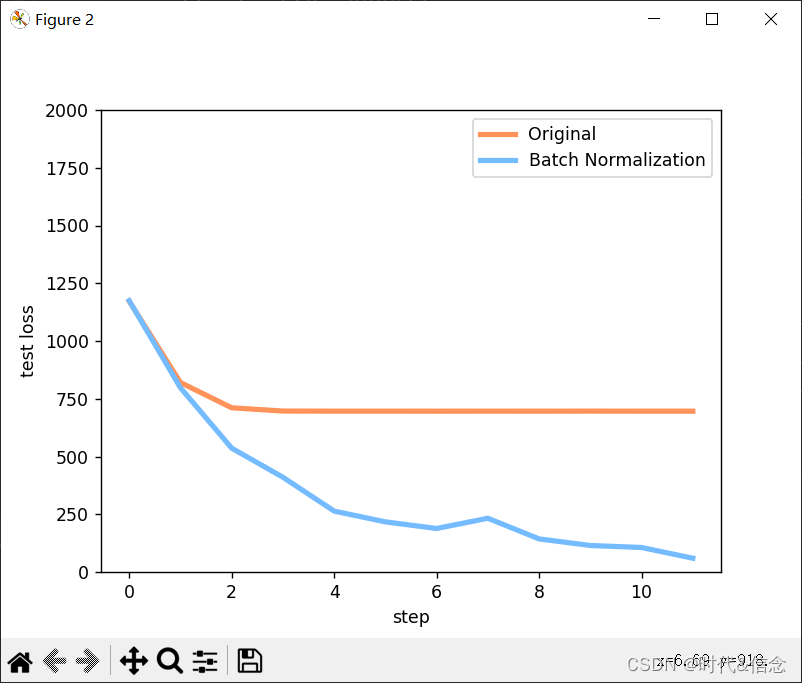
文章提出了基于soft-target的蒸馏方法,可以让学生模型学习到教师模型的预测概率分布,从而增强学生模型的泛化能力。实验表明,在MNIST和speech recognition数据上,基于soft target的学生模型可以提取到更多有用的信息,且可以有效防止过拟合的发生。
5. 原文传送门
Distilling the Knowledge in a Neural Network