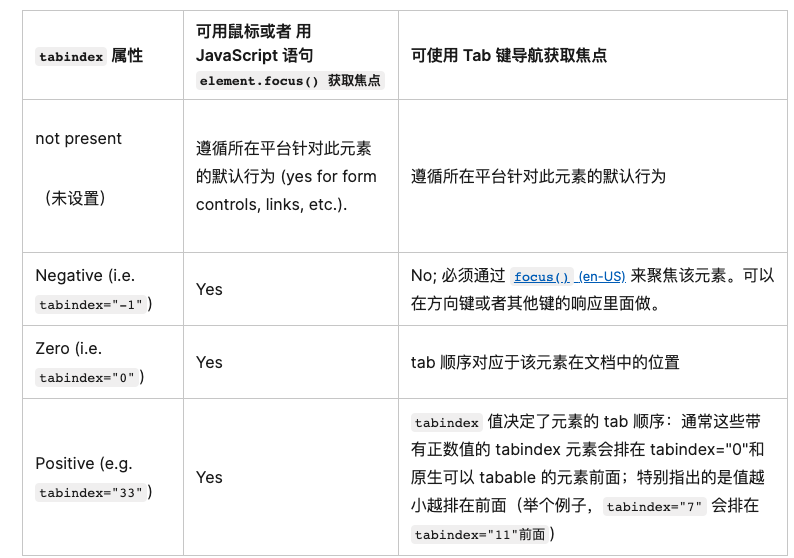
1.什么是KMP算法
解决字符串匹配问题；看文本串是否出现过模式串；
文本串：aabaabaaf;
模式串：aabaaf；
暴力解法：两层for循环，时间复杂度：O(m*n) m n分别是长度；
kmp解决：

f和b不匹配后（竖线），跳到模式串第一个b重新开始匹配；为啥跳b看下面

前缀表：b的前面是aa，后面也是aa，所以遇到不匹配的时候，就找前面最长前后缀；
aabaaf
前缀：包含首字母，不包含尾字母的所有子串；a aa aab aaba aabaa aabaaf;
后缀：包含尾字母，不包含首字母的所有子串；af aaf baaf abaaf
最长相等前后缀：a 0 aa 1 aab 0 aaba 1 aabaa 2 aabaaf 0
前缀表： 0 1 0 1 2 0 （上面数字） 2意味着有一个后缀aa ,前面有一个前缀aa。所以匹配从前缀的后面开始匹配，就是从b重新开始匹配；
next数组 或者prefix前缀表；
2.代码
next数组形式： 遇到冲突向前回退
左移一： -1 0 1 0 1 2；
整体减1 -1 0 -1 1 -1；

void getNext(int *next,char *s){
	//初始化i 后缀末尾 j前缀末尾,也代表i 包括i之前这个子串的最长相等前后缀的长度
	int j = 0;
	int next[0] = 0;
	int len = strlen(s);
	for(int i = 1; i < len; i++) {
		//前后缀不同
		while(s[i] != s[j] && j > 0) {
			j = next[j-1]; // j 回退
		}
	// 前后缀相同
	if(s[i] == s[j]){
	   j++;
	   // 更新next值
	  next[i] = j;
	  }
   }
 }

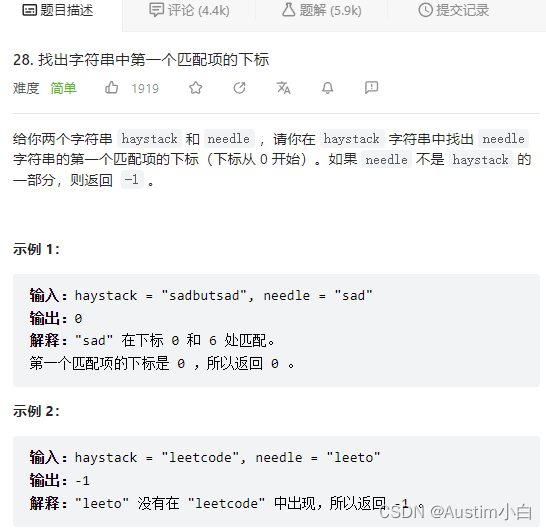
题目描述

//前缀表不减一版本
void getNext(int* next, char* s) {
    //初始化 next
    int j = 0;
    next[0] = j;
    for (int i = 1; i < strlen(s); i++) {	//注意 i 从 1 开始
        //若前后缀不相同
        while (j > 0 && s[i] != s[j]) {
            //则向前回退
            j = next[j - 1];
        }
        //若前后缀相同
        if (s[i] == s[j]) {
            //i 和 j 同时向后移动（i 的增加在 for 循环里）
            j++;
        }
        //将 j（前缀的长度）赋值给 next[i]
        next[i] = j;
    }
}

int strStr(char * haystack, char * needle){
    int len1 = strlen(haystack);
    int len2 = strlen(needle);
    //当 needle 为空字符串时，返回 0
    if (len2 == 0) {
        return 0;
    }

    //构建 next 数组
    int* next = malloc(sizeof(int) * len2);
    getNext(next, needle);
    //next 记录的起始位置为 0，所以这里也从 0 开始
    int j = 0;
    for (int i = 0; i < len1; i++) {	//注意匹配时 i 从 0 开始
        //若不匹配
        while (j > 0 && haystack[i] != needle[j]) {
            //j 退回到之前匹配的位置
            j = next[j - 1];
        }
        //若匹配
        if (haystack[i] == needle[j]) {
            //i 和 j 同时向后移动（i 的增加在 for 循环里）
            j++;
        }
        //当 j 等于 needle 的长度时，说明字符串 haystack 里出现了字符串 needle
        if (j == len2) {
            //返回 needle 字符串出现的第一个位置
            return (i - len2 + 1);
        }
    }
	
    //若未找到则说明不存在，返回 -1
    return -1;
}

题目描述

void CalcNext(char *p,int *next)
{
    next[0]=-1;
    int nlen = strlen(p);
    int k = -1;
    int j = 0;
    while (j < nlen) {
        if (k ==-1 || p[j] == p[k]) {
            ++k;
            ++j;
            next[j] = k;
        }
        else
        k = next[k];
    }
}
bool repeatedSubstringPattern(char * s){
    int length = strlen(s);
    int *next=(int *)malloc(sizeof(int)*(length+1));
    CalcNext(s,next);
    int k = next[length];
    int p = length-k;
    if(length%p == 0 && length != p)
    return true;
    return false;
}