位运算修行手册

news2024/11/24 16:41:02

*明明自觉学会了不少知识，可真正开始做题时，却还是出现了“一支笔，一双手，一道力扣（Leetcode）做一宿”的窘境？你是否也有过这样的经历，题型不算很难，看题解也能弄明白，可一到自己做就变成了与题面面相觑无从下手。这就是基础知识掌握不扎实、不牢固导致的，我们以位运算为例，我将把位运算基础给你清楚讲述，再以例题带你实战体验。

一、位与运算符

位与运算符是一个二元的位运算符，也就是有两个操作数，表示为 x & y。

位与运算会对操作数的每一位按照如下表格进行运算，对于每一位只有 0 或 1 两种情况，所以组合出来总共 4 种情况。

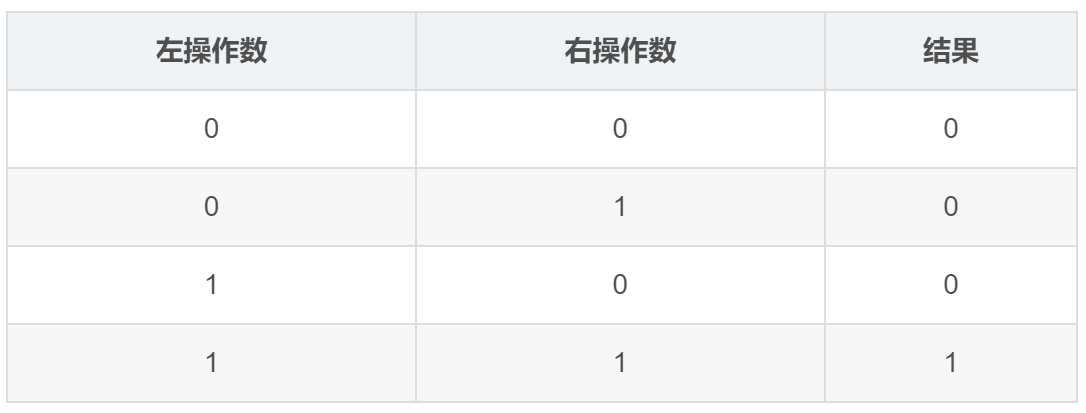
https://article-images.zsxq.com/FuK9MkdBw13Y-L9Hmp176jUtqoKi

通过这个表，我们得出一些结论：

1）无论是 0 或 1，只要位与上 1，还是它本身；

2）无论是 0 或 1，只要位与上 0，就变成 0；

所以对于位与来说，只要这一位上有一个 0，这一位的结果就会变成 0。

int main() {

    int a = 0b1010;

    int b = 0b0110;

    printf("%d\n", (a & b) );

    return 0;

}

  1. (1) 在C语言中，以 0b 作为前缀，表示这是一个二进制数。那么 a 的实际值就是 (1010) 。

  2. (2) 同样的， b 的实际值就是 (0110) ；

  3. (3) 那么这里 a & b 就是对 (1010) 和 (0110) 的每一位做表格中的 & 运算。

  4. 所以最后输出结果为：

  5. 因为输出的是十进制数，它的二进制表示为： (0010)_2。

  6. 注意：这里的 前导零 可有可无，作者写上前导零只是为了对齐以及让读者更加清楚位与的运算方式。

二、位与运算符的应用

1、奇偶性判定

  1. 我们判断一个数是奇数还是偶数，往往是通过取模 %来判断的，如下：
int main() {

    if(5 % 2 == 1) {

        printf("5是奇数\n");

    }

    if(6 % 2 == 0) {

        printf("6是偶数\n");

    }

    return 0;

}
  1. 然而，我们也可以这么写：
int main() {

    if(5 & 1) {

        printf("5是奇数\n");

    }

    if( (6 & 1) == 0 ) {

        printf("6是偶数\n");

    }

    return 0;

}

1.
  1. 这是利用了奇数和偶数分别的二进制数的特性，如下表所示：

https://article-images.zsxq.com/Fr3FEevcsw6AGwMedmlYozR8fBWD

  1. 所以，我们对任何一个数，通过将它和 0b1 进行位与，结果为零，则必然这个数的二进制末尾位为0，根据以上表就能得出它是偶数了；否则，就是奇数。

  2. 注意，由于 if 语句我们还没有实际提到过，所以这里简单提一下，后面会有系统的讲解：

  3. 对于以上语句，expr 代表的是一个表达式，表达式的值最后只有 零 或 非零，如果值为非零，才会执行 body中的内容。

2、取末五位

【例题1】给定一个数，求它的二进制表示的末五位，以十进制输出即可。

  1. 这个问题的核心就是：我们只需要末五位，剩下的位我们是不需要的，所以可以将给定的数 位与上0b11111，这样一来就直接得到末五位的值了。

  2. 代码实现如下：

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", (x & 0b11111) );

    return 0;

}

那么如果问题变成下面的形式，代码又要怎么写呢？

【例题2】如果是想得到末七位、末九位、末十四位、末 K 位，应该如何实现呢？

3、消除末尾五位

【例题3】给定一个 32 位整数，要求消除它的末五位。

  1. 还是根据位与的性质，消除末五位的含义，有两层：

  2. 1）末五位，要全变成零；

  3. 2）剩下的位不变；

  4. 那么，根据位运算的性质，我们需要数，它的高27位都为1，低五位都为 0，则这个数就是：

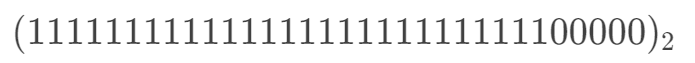
https://article-images.zsxq.com/Fgop5R_LxyZtPF70Vs-VdDN51j_x

  1. 但是如果要这么写，代码不疯掉，人也会疯掉，所以一般我们把它转成十六进制，每四个二进制位可以转成一个十六进制数，所以得到十六进制数为 0xffffffe0。

  2. 代码实现如下：

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", (x & 0xffffffe0) );

    return 0;

}

提示： f 代表 4 个1； e 代表 3个1,1个0； 0 代表 4 个 0；

4、消除末尾连续1

【例题4】给出一个整数，现在要求将这个整数转换成二进制以后，将末尾连续的1都变成0，输出改变后的数（以十进制输出即可）。

  1. 我们知道，这个数的二进制表示形式一定是：

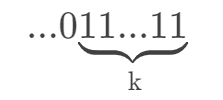
https://article-images.zsxq.com/FjNYjX6GoiKRmv13CEGybKCt0Qe5

  1. 如果，我们把这个二进制数加上1，得到的就是：

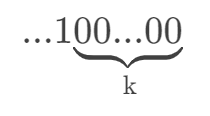
https://article-images.zsxq.com/FjFgw6gfXY6yEU2lGniGHpOVdaL4

  1. 我们把这两个数进行位与运算，得到：

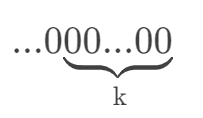
https://article-images.zsxq.com/FivTjeFY443LOb1bqqNav9LkrIpD

  1. 所以，你学会了吗？

5、2的幂判定

【例题5】请用一句话，判断一个正数是不是2的幂。

  1. 如果一个数是 2 的幂，它的二进制表示必然为以下形式：

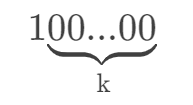
https://article-images.zsxq.com/FuSMvHw-X3ZrceocHXM8XJQvjkY2

  1. 这个数的十进制值为 2 的 k 次。

  2. 那么我们将它减一，即 2 的 k 次 减一 的二进制表示如下（参考二进制减法的借位）：

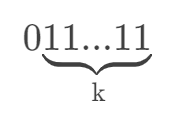
https://article-images.zsxq.com/Fp4a8QJapXNc0ry4bnQ3yEhYc5fY

  1. 于是 这两个数位与的结果为零，于是我们就知道了如果一个数 x 是 2 的幂，那么 x & (x-1) 必然为零。而其他情况则不然。所以本题的答案为：

三、位或运算符

位或运算符是一个二元的位运算符，也就是有两个操作数，表示为 x | y。位或运算会对操作数的每一位按照如下表格进行运算，对于每一位只有 0 或 1 两种情况，所以组合出来总共 4 种情况。

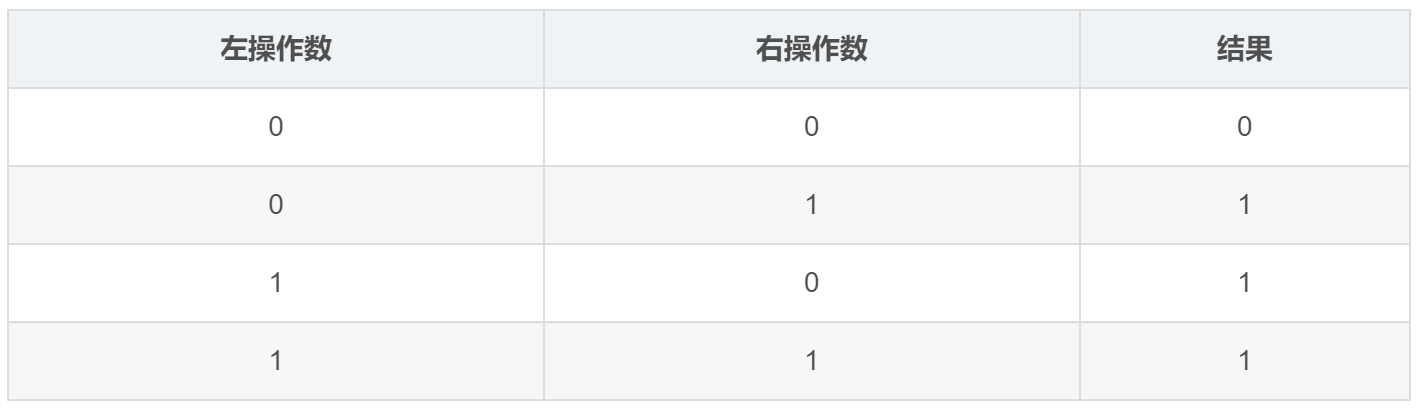
https://article-images.zsxq.com/FvpY3Ck4J9BVcaWPDjwehJJbclwg

通过这个表，我们得出一些结论：

1）无论是 0 或 1，只要位或上 1，就变成1；

2）只有当两个操作数都是0的时候，才变成 0；

int main() {

    int a = 0b1010;

    int b = 0b0110;

    printf("%d\n", (a | b) );

    return 0;

}

(1) 在C语言中，以 0b 作为前缀，表示这是一个二进制数。那么 a 的实际值就是 (1010);

(2) 同样的，b 的实际值就是 (0110)；

(3) 那么这里 a | b 就是对 (1010) 和 (0110) 的每一位做表格中的 | 运算。

所以最后输出结果为：

因为输出的是十进制数，它的二进制表示为： (1110)。

四、位或运算符的应用

1、设置标记位

【例题1】给定一个数，判断它二进制低位的第 5 位，如果为 0，则将它置为 1。

这个问题，我们很容易联想到位或。我们分析一下题目意思，如果第 5 位为 1，不用进行任何操作；如果第 5 位为 0，则置为 1。言下之意，无论第五位是什么，我们都直接置为 1 即可，代码如下：

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", x | 0b10000);

    return 0;

}

2、置空标记位

【例题2】给定一个数，判断它二进制低位的第 5 位，如果为 1，则将它置为 0。

当我们学过位与以后，很容易得出这样一种做法：

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", x & 0b11111111111111111111111111101111);

    return 0;

}

其它位不能变，所以 位与 上1；第5位要置零，所以 位与 上0；这样写有个问题，就是这串数字太长了，一点都不美观，而且容易写错，当然我们也可以转换成 十六进制，转换的过程也有可能出错。

而我们利用位或，只能将第5位设置成1，怎么把它设置成0呢？

我们可以配合减法来用。分成以下两步：

1）首先，强行将低位的第5位置成1；

2）然后，强行将低位的第5位去掉；

第 (1) 步可以采用位或运算，而第 (2) 步，我们可以直接用减法即可。代码实现如下：

int main() {

    int x;

    int a = 0b10000;

    scanf("%d", &x);

    printf("%d\n", (x | a) - a );

    return 0;

}

注意：直接减是不行的，因为我们首先要保证那一位为 1，否则贸然减会产生借位，和题意不符。

3、低位连续零变一

【例题3】给定一个整数 x，将它低位连续的 0 都变成 1。

假设这个整数低位连续有 k 个零，二进制表示如下：

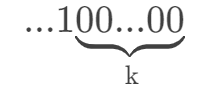
https://article-images.zsxq.com/FiPsRdLga5cfh8-4OBQc7DIMfrKD

那么，如果我们对它进行减一操作，得到的二进制数就是：

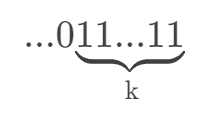
https://article-images.zsxq.com/Fr1cTE2CXyRhlBgZUPFfJRwwDG56

我们发现，只要对这两个数进行位或，就能得到：

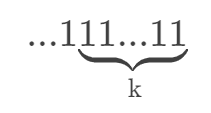
https://article-images.zsxq.com/Fi4GQ3jvcIupCmwF3tDYwl1_fjKC

也正是题目所求，所以代码实现如下：

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", x | (x-1) );

    return 0;

}

(1) x | (x-1) 就是题目所求的 “低位连续零变一” 。

4、低位首零变一

【例题4】给定一个整数 x，将它低位第一个 0 变成 1。

记得在评论区留下你的答案哦 ~

五、异或运算符

异或运算符是一个二元的位运算符，也就是有两个操作数，表示为 x ^ y。

异或运算会对操作数的每一位按照如下表格进行运算，对于每一位只有 0 或 1 两种情况，所以组合出来总共 4 种情况。

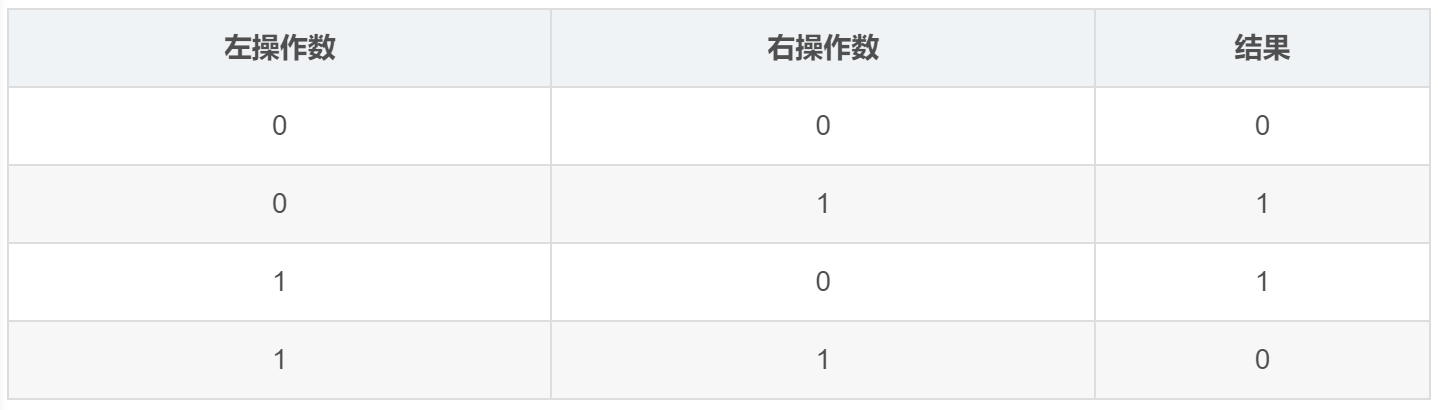
https://article-images.zsxq.com/FiBrFELi58vEcQmME5_CcnoTv5dW

通过这个表，我们得出一些结论：

1）两个相同的十进制数异或的结果一定为零。

2）任何一个数和 0 的异或结果一定是它本身。

3）异或运算满足结合律和交换律。

int main() {

    int a = 0b1010;

    int b = 0b0110;

    printf("%d\n", (a ^ b) );

    return 0;

}

(1) 在C语言中，以 0b 作为前缀，表示这是一个二进制数。那么 a 的实际值就是 (1010) 。

(2) 同样的， b 的实际值就是 (0110) ；

(3) 那么这里 a ^ b 就是对 (1010) 和 (0110) 的每一位做表格中的 ^ 运算。

所以最后输出结果为：

因为输出的是十进制数，它的二进制表示为： (1100)。

六、异或运算符的应用

1、标记位取反

【例题1】给定一个数，将它的低位数起的第 4 位取反，0 变 1，1 变 0。

这个问题，我们很容易联想到异或。我们分析一下题目意思，如果第 4 位为 1，则让它异或上 0b1000 就能变成 0；如果第 4 位 为 0，则让它异或上 0b1000 就能变成 1，也就是无论如何都是异或上 0b1000 ，代码如

int main() {

    int x;

    scanf("%d", &x);

    printf("%d\n", x ^ 0b1000);

    return 0;

}

2、变量交换

【例题2】给定两个数 a 和 b，用异或运算交换它们的值。

这个是比较老的面试题了，直接给出代码：

int main() {

    int a, b;

    while (scanf("%d %d", &a, &b) != EOF) {

        a = a ^ b;

        b = a ^ b;

        a = a ^ b;

        printf("%d %d\n", a, b);

    }

    return 0;

}

我们直接来看 (1) 和 (2) 这两句话，相当于 b 等于 a ^ b ^ b ，根据异或的几个性质，我们知道，这时候的 b 的值已经变成原先 a 的值了。

而再来看第 (3) 句话，相当于 a 等于 a ^ b ^ a，还是根据异或的几个性质，这时候，a 的值已经变成了原先 b 的值。

从而实现了变量 a 和 b 的交换。

3、出现奇数次的数

【例题3】输入 n 个数，其中只有一个数出现了奇数次，其它所有数都出现了偶数次。求这个出现了奇数次的数。

根据异或的性质，两个一样的数异或结果为零。也就是所有出现偶数次的数异或都为零，那么把这 n 个数都异或一下，得到的数就一定是一个出现奇数次的数了。

int main() {

    int n, x, i, ans;

    scanf("%d", &n);

    ans = 0;

    for(i = 0; i < n; ++i) {

        scanf("%d", &x);

        ans = (ans ^ x);

    }

    printf("%d\n", ans);

    return 0;

}

4、丢失的数

【例题4】给定一个 n-1 个数，分别代表 1 到 n 的其中 n-1 个，求丢失的那个数。

记得在评论区留下你的答案哦 ~

5、简单加密

基于 两个数异或为零，任何数和零异或为其本身 这两个特点，异或还可以用来做简单的加密。将明文异或上一个固定的数变成密文以后，可以通过继续异或上这个数，再将密文转变成明文。

七、按位取反运算符

取反运算符是一个单目位运算符，也就是只有一个操作数，表示为 ~x。取反运算会对操作数的每一位按照如下表格进行运算，对于每一位只有 0 或 1 两种情况。

https://article-images.zsxq.com/FqGHMjJbeJzIbbRMwyx6vVUtpGbP

int main() {

    int a = 0b1;

    printf("%d\n", ~a );

    return 0;

}

这里 ~a 代表的是对二进制数 1 进行取反，直观感受应该是 0。但是实际输出的却是：

-2

这是为什么呢？那是因为，这是一个 32 位整数，实际的取反操作是这样的：
00000000 00000000 00000000 00000001

11111111 11111111 11111111 11111110

32位整数的二进制表示，前导零也要参与取反。而对于一个有符号的 32 位整数，我们需要用最高位来代表符号位，即最高位为 0，则代表正数；最高位为 1，则代表负数；

这时候我们就需要引入补码的概念了。

1、补码的概念

在计算机中，二进制编码是采用补码的形式表示的，补码定义如下：

正数的补码是它本身，符号位为 0；负数的补码为正数数值二进制位取反后加一，符号位为一；

2、补码举例

根据补码的定义，-2的补码计算，需要经过两步：

1）对 2 的二进制进行按位取反，如下：
00000000 00000000 00000000 00000010

11111111 11111111 11111111 11111101

2）然后加上 1，如下：

11111111 11111111 11111111 11111101

  • 00000000 00000000 00000000 00000001

11111111 11111111 11111111 11111110

结果正好为我们开始提到的 ~1 的结果。

3、补码的真实含义

补码的真实含义，其实体现在 “补” 这个字上，在数学上，两个互为相反数的数字相加等于 0，而在计算机中，两个互为相反数的数字相加等于 2 的 n 次。

换言之，互为相反数的两个数互补，补成 2 的 n 次。

对于 32位整型，n = 32；对于 64 位整型，n = 64。所以补码也可以表示成如下形式：

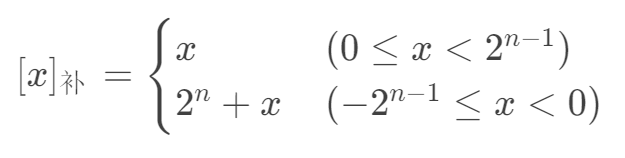
https://article-images.zsxq.com/FtYp9xvEhlduj1YtCnEf0vB1UBwf

于是，对于 int 类型，就有：

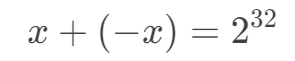
https://article-images.zsxq.com/Fv6q2Vd9LSbDZwSCdHhlaf6xKqP3

即：

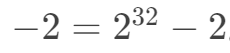
https://article-images.zsxq.com/Fh68gYeZdzO0W4Dmw6pwnO02h09n

于是，我们开始数数……

2^32 = 1 00000000 00000000 00000000 00000000

2^32 - 1 = 11111111 11111111 11111111 11111111

2^32 - 2 = 11111111 11111111 11111111 11111110

近一步了解了 -2 的二进制表示。

八、按位取反运算符的应用

1、0 的取反

【例题1】0 的取反结果为多少呢？

首先对原码进行取反，得到：
00000000 00000000 00000000 00000000

11111111 11111111 11111111 11111111

这个问题，我们刚讨论完，这个答案为 2^32 - 1。但是实际输出时，你会发现，它的值是 -1 。

这是为什么？

原因是因为在C语言中有两种类型的 int ，分别为 unsigned int 和 signed int ，我们之前讨论的 int 都是 signed int 的简称。

1）有符号整型

对于有符号整型 signed int 而言，最高位表示符号位，所以只有 31 位能表示数值，能够表示的数值范围是：

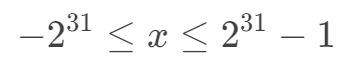
https://article-images.zsxq.com/Fi0lx3D7DTuL6VbpSvjuj4KSYb_q

所以，对于有符号整型，输出采用 %d ，如下：

int main() {

    printf("%d\n", ~0 );

    return 0;

}

结果为：

-1

2）无符号整型

对于无符号整型 unsigned int 而言，由于不需要符号位，所以总共有32位表示数值，数值范围为：

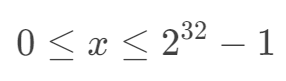
https://article-images.zsxq.com/Fvrxl2rj6EjwUVfXT6rgAmcrhLlu

对于无符号整型，输出采用 %u ，如下：

int main() {

    printf("%u\n", ~0 );

    return 0;

}

结果为：

4294967295

即 2^ 32 - 1 。

2、相反数

【例题2】给定一个 int 类型的正数 x ，求 x 的相反数（注意：不能用负号）。

这里，我们可以直接利用补码的定义，对于正数 x ，它的相反数的补码就是 x 二进制取反加一。即： ~x + 1 。

int main() {

    int x = 18;

    printf("%d\n", ~x + 1 );

    return 0;

}

运行结果如下：

-18

3、代替减法

【例题3】给定两个 int 类型的正数 x 和 y，实现 x - y（注意：不能用减号）。

这个问题比较简单，如果上面的相反数已经理解了，那么， x - y 其实就可以表示成 x + (-y) ，而 -y 又可以表示成 ~y + 1 ，所以减法 x - y 就可以用 x + ~y + 1 来代替。

  • 代码实现如下：
int main() {

    int a = 8;

    int b = 17;

    printf("%d\n", a + ~b + 1 );

    return 0;

}

运行结果为：

-9

4、代替加法

【例题4】给定两个 int 类型的正数 x 和 y ，实现 x + y （注意：不能用加号）。

我们可以把 x + y 变成 x - (-y) ，而 -y 又可以替换成 ~y + 1 ；

所以 x + y 就变成了 x - ~y - 1 ，不用加号实现了加法运算。

int main() {

    int x = 18;

    int y = 7;

    printf("%d\n", x - ~y - 1 );

    return 0;

}

运行结果为：

25

九、左移运算符

1、左移的二进制形态

左移运算符是一个二元的位运算符，也就是有两个操作数，表示为 x << y 。其中 x 和 y 均为整数。

x << y 念作：“将 x 左移 y 位”，这里的位当然就是二进制位了，那么它表示的意思也就是：先将 x 用二进制表示，然后再左移 y 位，并且在尾部添上 y 个零。

举个例子：对于二进制数 (10111) 左移 y 位的结果就是：

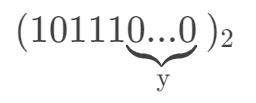
https://article-images.zsxq.com/FvTqe04ZHua0EeVeUMDCtMNXzo7n

2、左移的执行结果

x << y 的执行结果等价于：

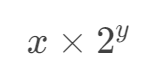
https://article-images.zsxq.com/Fk_rdCU_5WjxTh_orJIHhEnrhKuY

如下代码：

int main() {

    int x = 3;

    int y = 5;

    printf("%d\n", x << y);

    return 0;

}

输出结果为：

正好符合这个左移运算符的实际含义：

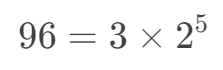
https://article-images.zsxq.com/FhtmddBPBXDrRnnKt9ntJl1rZJmd

最常用的就是当 x = 1 时，1 << y 代表的就是 2^y，即 2 的幂。

3、负数左移的执行结果

所谓负数左移，就是 x << y 中，当 x 为负数的情况，代码如下：

int main() {

    printf("%d\n", -1 << 1);

    return 0;

}

它的输出如下：

我们发现同样是满足的，这个可以用补码来解释，-1的补码为：

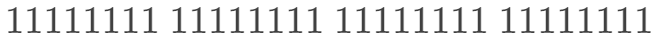
https://article-images.zsxq.com/FhggBS-a-eEd_69rLowsn9EhEwrw

左移一位后，最高位的 1 就没了，低位补上 0，得到：

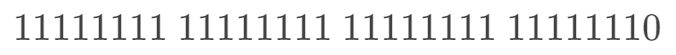
https://article-images.zsxq.com/Fs8_QTeR0VEbB_61OllhxoRrPCj5

而这，正好是 -2 的补码，同样，继续左移 1 位，得到：

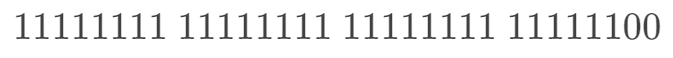
https://article-images.zsxq.com/FghDxL2eqaV_gY91WKkqtWjZeWXD

这是 -4 的补码，以此类推，所以负整数的左移结果同样也是满足的。

可以理解成 - (x << y) 和 (-x) << y 是等价的。

4、左移负数位是什么情况

刚才我们讨论了 x < 0 的情况，那么接下来，我们试下 y < 0 的情况会是如何？

是否同样满足如下等式呢？

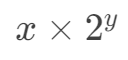
https://article-images.zsxq.com/FpFGvQNEhi_LQJq9OXWCaJhd4O89

如果还是满足，那么两个整数的左移就有可能产生小数了。

看个例子：

int main() {

    printf("%d\n", 32 << -1);

    printf("%d\n", 32 << -2);

    printf("%d\n", 32 << -3);

    printf("%d\n", 32 << -4);

    printf("%d\n", 32 << -5);

    printf("%d\n", 32 << -6);

    printf("%d\n", 32 << -7);

    return 0;

}

虽然能够正常运行，但是结果好像不是我们期望的，而且会报警告如下：

[Warning] left shift count is negative [-Wshift-count-negative]

实际上，编辑器告诉我们尽量不用左移的时候用负数，但是它的执行结果不能算错误，起码例子里面对了，结果不会出现小数，而是取整了。

左移负数位其实效果和右移对应正数数值位一致。

5、左移时溢出会如何

我们知道， int 类型的数都是 32 位的，最高位代表符号位，那么假设最高位为 1，次高位为 0，左移以后，符号位会变成 0，会产生什么问题呢？

举个例子，对于 -2^31 + 1 的二进制表示为：最高位和最低位为 1，其余为零。

int main() {

    int x = 0b10000000000000000000000000000001;

    printf("%d\n", x);

    return 0;

}

输出结果为：

那么，将它进行左移一位以后，得到的结果是什么呢？

int main() {

    int x = 0b10000000000000000000000000000001;

    printf("%d\n", x << 1);

    return 0;

}

我们盲猜一下，最高位的 1 被移出去，最低位补上 0，结果应该是 0b10 。

实际输出的结果，的确是：

但是如果按照之前的规则，答案应该是：

https://article-images.zsxq.com/FmKoYtppTNqzNexloHYWWhCUIcxn

这里又回到了补码的问题上，事实上，在计算机中， int 整型其实是一个环，溢出以后又会回来，而环的长度正好是 2^32，所以 -2^32 + 2 = 2，这个就有点像同余的概念，这两个数是模 2^32 同余的。

十、左移运算符的应用

1、取模转化成位运算

对于 x 模上一个 2 的次幂的数 y，我们可以转换成位与上 2^y-1。

即在数学上的：

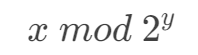
https://article-images.zsxq.com/FpUvtfkgp_qUoKYkLHViqWqgeTgD

在计算机中就可以用一行代码表示：x & ((1 << y) - 1)。

2、生成标记码

我们可以用左移运算符来实现标记码，即 1 << k 作为第 k 个标记位的标记码，这样就可以通过一句话，实现对标记位置 0、置 1、取反等操作。

1）标记位置1

【例题1】对于 x 这个数，我们希望对它二进制位的第 k 位（从0开始，从低到高数）置为 1。

置 1 操作，让我们联想到了 位或 运算。

它的特点是：位或上 1，结果为 1；位或上0，结果不变。

所以我们对标记码的要求是：第 k 位为 1，其它位为 0，正好是 (1 << k) ，那么将 第 k 位 置为 1 的语句可以写成：x | (1 << k)。

2）标记位置0

【例题2】对于 x 这个数，我们希望对它二进制位的第 k 位（从0开始，从低到高数）置为 0。

置 0 操作，让我们联想到了 位与 运算。

它的特点是：位与上 0，结果为 0；位与上 1，结果不变。

所以在我们对标记码的要求是：第 k 位为 0，其它位为 1，我们需要的是 (~(1 << k))，那么将 第 k 位 置为 0 的语句可以写成：x & (~(1 << k))。

3）标记位取反

【例题3】对于 x 这个数，我们希望对它二进制位的第 k 位（从0开始，从低到高数）取反。

取反操作，联想到的是 异或 运算。

它的特点是：异或上 1，结果取反；异或上 0，结果不变。

所以我们对标记码的要求是：第 k 位为1，其余位为 0，其值为 (1 << k) 。那么将 第 k 位 取反的语句可以写成： x ^ (1 << k) 。

3、生成掩码

同样，我们可以用左移来生成一个掩码，完成对某个数的二进制末 k 位执行一些操作。

对于 (1 << k) 的二进制表示为：1 加上 k 个 0，那么 (1 << k) - 1 的二进制则代表 k 个 1。

把末尾的 k 位都变成 1，可以写成：x | ((1 << k) - 1)。

把末尾的 k 为都变成 0，可以写成：x & ~((1 << k) - 1)。

把末尾的 k 位都取反，可以写成：x ^ ((1 << k) - 1)。

十一、右移运算符

1、右移的二进制形态

右移运算符是一个二元的位运算符，也就是有两个操作数，表示为 x >> y。其中 x 和 y 均为整数。

x >> y 念作：“将 x 右移 y 位”，这里的位当然就是二进制位了，那么它表示的意思也就是：先将 x 用二进制表示，对于正数，右移 y 位；对于负数，右移 y 位后高位都补上 1。

举个例子：对于十进制数 87，它的二进制是 (1010111)， 左移 y 位的结果就是：

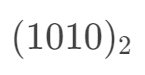
https://article-images.zsxq.com/FvInA6fe5nYR4n5vi7lWXfKy8S9F

2、右移的执行结果

x >> y 的执行结果等价于：

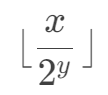
https://article-images.zsxq.com/FkeAdR01NS5ApAkj5EjHYz-zUNjc

这个符号代表取下整。如下代码：

int main() {

    int x = 0b1010111;

    int y = 3;

    printf("%d\n", x >> y);

    return 0;

}

输出结果为：

正好符合这个右移运算符的实际含义：

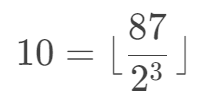
https://article-images.zsxq.com/Funy2VkX9ZHf-H9VFUc3_NALCVY9

由于除法可能造成不能整除，所以才会有 取下整 这一步运算。

3、负数右移的执行结果

所谓负数右移，就是 x >> y 中，当 x 为负数的情况，代码如下：

int main() {

    printf("%d\n", -1 >> 1);

    return 0;

}

它的输出如下：

我们发现同样是满足如下式子的

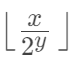
https://article-images.zsxq.com/FhOdztoufxwrir271BznnGYfmtgE

这个可以用补码来解释，-1 的补码为：

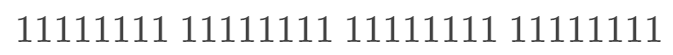
https://article-images.zsxq.com/Fj-tKcTGYyQW68iOIqXEpvtPyWpe

右移一位后，由于是负数，高位补上 1，得到：

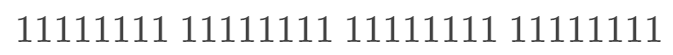
https://article-images.zsxq.com/Fj-tKcTGYyQW68iOIqXEpvtPyWpe

可以理解成 - (x >> y）和 (-x) >> y 是等价的。

然后我们来简单做道题巩固一下

【例题1】要求不运行代码，肉眼看出这段代码输出多少。



int main() {

    int x = (1 << 31) | (1 << 30) | 1;

    int y = (1 << 31) | (1 << 30) | (1 << 29);

    printf("%d\n", (x >> 1) / y);

    return 0;

}

4、右移负数位是什么情况

刚才我们讨论了 x < 0 的情况，那么接下来，我们试下 y < 0 的情况会是如何？是否同样满足如下性质呢？

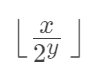
https://article-images.zsxq.com/FkIn8OfkxIBaXIrLHlWwvfSXfEcT

如果还是满足，那么两个整数的左移就有可能产生小数了。

看个例子：

int main() {

    printf("%d\n", 1 >> -1);

    printf("%d\n", 1 >> -2);

    printf("%d\n", 1 >> -3);

    printf("%d\n", 1 >> -4);

    printf("%d\n", 1 >> -5);

    printf("%d\n", 1 >> -6);

    printf("%d\n", 1 >> -7);

    return 0;

}

虽然能够正常运行，但是结果好像不是我们期望的，而且会报警告如下：

[Warning] right shift count is negative [-Wshift-count-negative]

实际上，编辑器告诉我们尽量不用右移的时候用负数，但是它的执行结果不能算错误，起码例子里面对了。

右移负数位其实效果和左移对应正数数值位一致。

十二、右移运算符的应用

1、去掉低 k 位

【例题2】给定一个数 x，去掉它的低 k 位以后进行输出。

这个问题，可以直接通过右移来完成，如下：x >> k。

2、取低位连续 1

【例题3】获取一个数 x 低位连续的 1 并且输出。

对于一个数 x，假设低位有连续 k 个 1。如下：

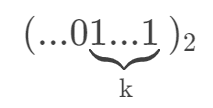
https://article-images.zsxq.com/Fsl9kFfLcoD6dd_P2bwxA3RjTP0q

然后我们将它加上 1 以后，得到的就是：

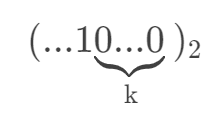
https://article-images.zsxq.com/Fs_N8KlpKEMMQH1lwFA5g0uVdVuU

这时候将这两个数异或结果为：

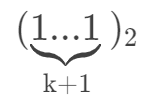
https://article-images.zsxq.com/FiBtxZ6AnUcJQFN2r97bOPbR-Wwc

这时候，再进行右移一位，就得到了 连续 k 个 1 的值，也正是我们所求。

所以可以用以下语句来求：(x ^ (x + 1)) >> 1。

3、取第k位的值

【例题4】获取一个数 x 的第 k(0 <= k <= 30) 位的值并且输出。

对于二进制数来说，第 k 位的值一定是 0 或者 1。

而 对于 1 到 k-1 位的数字，对于我们来说是没有意义的，我们可以用右移来去掉，再用位与运算符来获取二进制的最后一位是 0 还是 1，如下：(x >> k) & 1。

那么接下来，我们试下 y < 0 的情况会是如何？是否同样满足如下性质呢？

[外链图片转存中…(img-3wbr0PBV-1690102819771)]

如果还是满足，那么两个整数的左移就有可能产生小数了。

看个例子：

int main() {

    printf("%d\n", 1 >> -1);

    printf("%d\n", 1 >> -2);

    printf("%d\n", 1 >> -3);

    printf("%d\n", 1 >> -4);

    printf("%d\n", 1 >> -5);

    printf("%d\n", 1 >> -6);

    printf("%d\n", 1 >> -7);

    return 0;

}

虽然能够正常运行，但是结果好像不是我们期望的，而且会报警告如下：

[Warning] right shift count is negative [-Wshift-count-negative]

实际上，编辑器告诉我们尽量不用右移的时候用负数，但是它的执行结果不能算错误，起码例子里面对了。

右移负数位其实效果和左移对应正数数值位一致。

十二、右移运算符的应用

1、去掉低 k 位

【例题2】给定一个数 x，去掉它的低 k 位以后进行输出。

这个问题，可以直接通过右移来完成，如下：x >> k。

2、取低位连续 1

【例题3】获取一个数 x 低位连续的 1 并且输出。

对于一个数 x，假设低位有连续 k 个 1。如下：

[外链图片转存中…(img-d1hKcnX3-1690102819771)]

然后我们将它加上 1 以后，得到的就是：

[外链图片转存中…(img-5VGxiKFY-1690102819772)]

这时候将这两个数异或结果为：

[外链图片转存中…(img-4z96Jhpo-1690102819772)]

这时候，再进行右移一位，就得到了 连续 k 个 1 的值，也正是我们所求。

所以可以用以下语句来求：(x ^ (x + 1)) >> 1。

3、取第k位的值

【例题4】获取一个数 x 的第 k(0 <= k <= 30) 位的值并且输出。

对于二进制数来说，第 k 位的值一定是 0 或者 1。

而 对于 1 到 k-1 位的数字，对于我们来说是没有意义的，我们可以用右移来去掉，再用位与运算符来获取二进制的最后一位是 0 还是 1，如下：(x >> k) & 1。

十三 leecode相关题

191. 位1的个数

解题思路：

  1. 初始化计数器变量 count 为 0。
  2. 定义一个循环变量 i，并初始化为 0。
  3. 进入循环，判断 i 是否小于 32（因为无符号整数有 32 位）。
  4. 在循环内部，首先使用位运算将数字 n 的第 i 位设置为 1，并将结果与 n 进行比较。如果结果等于 n，则说明第 i 位为 1，将计数器 count 加 1。
  5. 循环变量 i 增加 1，继续下一次循环。
  6. 循环结束后，返回最终的计数值 count。
class Solution {
public:
    int hammingWeight(uint32_t n) {
        int count=0;
        uint32_t i=0;
        while(i<32)
        {
            if((n | (1<<i)) == n)count++;

            i++;
        }
        return count;
    }
};

201. 数字范围按位与

解题思路：

  1. 初始化计数器变量 count 为 0。
  2. 进入循环，判断 left 是否小于 right。
  3. 在循环内部，将 left 和 right 都右移一位（相当于除以 2），并同时增加计数器 count。
  4. 循环结束后，返回 left 左移 count 位的结果。
class Solution {
public:
    int rangeBitwiseAnd(int left, int right) {
        int count=0;
        while(left<right)
        {
            left>>=1;
            right>>=1;
            ++count;
        }
        return left<<count;
    }
};

剑指 Offer 56 - II. 数组中数字出现的次数 II

解题思路：

  1. 初始化一个长度为 32 的数组 count，用于统计每一位上的出现次数。
  2. 初始化结果变量 result 为 0。
  3. 进入第一个循环，循环变量 i 控制当前统计的是第 i 位。
  4. 在第一个循环内部，进入第二个循环，循环变量 num 遍历数组 nums 中的每个元素。
  5. 在第二个循环内部，通过右移 i 位和按位与运算，将 num 的第 i 位取出并累加到 count[i] 中，即统计当前位上数字出现的次数。
  6. 循环结束后，进入第三个循环，循环变量 i 控制当前统计的是第 i 位。
  7. 在第三个循环内部，通过对 count[i] 取余 3，得到只出现一次的数字在当前位上的值，并将其左移 i 位后，通过按位或运算更新结果变量 result。
  8. 循环结束后，返回最终的结果变量 result。

class Solution {
public:
    int singleNumber(std::vector<int>& nums) {
        int count[32] = {0}; // 用于统计每一位上的出现次数
        int result = 0;

        for (int i = 0; i < 32; i++) {
            for (int num : nums) {
                // 统计当前位上数字出现的次数
                count[i] += (num >> i) & 1;
            }

            // 对统计结果取余，得到只出现一次的数字在当前位上的值
            result |= (count[i] % 3) << i;
        }

        return result;
    }
};

982. 按位与为零的三元组

解题思路：

  1. 初始化结果变量 ans 为 0。
  2. 初始化长度为 2^16（即65536）的数组 count，用于统计每个数字的按位与结果出现的次数。
  3. 进入第一个循环，循环变量 x 遍历数组 nums 中的每个元素。
  4. 在第一个循环内部，进入第二个循环，循环变量 y 遍历数组 nums 中的每个元素。
  5. 在第二个循环内部，通过按位与运算符将 x 和 y 按位与的结果作为索引，将 count 对应位置的值增加 1，以统计每个按位与结果出现的次数。
  6. 第二个循环结束后，进入第三个循环，循环变量 x 遍历数组 nums 中的每个元素。
  7. 在第三个循环内部，进入第四个循环，循环变量 i 遍历从 0 到 2^16-1 的所有整数。
  8. 在第四个循环内部，判断是否满足 (x & i) == 0 的条件，如果满足，则将 count[i] 的值累加到结果变量 ans 中。
  9. 第四个循环结束后，返回最终的结果变量 ans。
class Solution {
public:
    int countTriplets(vector<int>& nums) {
        int ans=0;
        int count[1<<16]={0};
        for(int x:nums)
            for(int y:nums)
                count[x&y]++;
        
        for(int x:nums)
            for(int i=0;i<1<<16;++i)
                if((x&i)==0)ans+=count[i];
        return ans;
    }
};

1835. 所有数对按位与结果的异或和

解题思路：

  1. 我们需要将数组arr1中的所有元素进行异或运算，得到一个变量a作为中间结果。这是因为异或运算满足结合律和交换律，即无论元素的顺序如何，结果都是相同的。

  2. 我们需要遍历数组arr2中的每个元素，并对其进行按位与运算，将结果保存回数组arr2中。这样做的目的是将arr2中的每个元素与a进行按位与运算，从而获取每个(i, j)数对的按位与结果。

  3. 我们再次遍历数组arr2，对其中的每个元素进行异或运算，得到最终的异或和ans。

  4. 我们只需要进行两次循环来完成计算，分别是遍历arr1和遍历arr2的过程，因此时间复杂度为O(N+M)，其中N是arr1的长度，M是arr2的长度。

  5. 这样写的原因是为了利用异或运算的性质，同时减少了额外空间的使用，直接在原数组arr2上进行操作。这样可以提高代码的效率和节省内存空间。

class Solution {
public:
    int getXORSum(vector<int>& arr1, vector<int>& arr2) {
        //(a&b)^(a&c)=a&(b^c)
        int ans=0,a=0;
        for(int i=0;i<arr1.size();++i){a^=arr1[i];}
        for(int i=0;i<arr2.size();++i){arr2[i]&=a;}
        for(int i=0;i<arr2.size();++i){ans^=arr2[i];}
        return ans;
    }
};

后记

刷题最重要的是基础！基础！基础！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/784055.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Spring中事务失效的8中场景

Spring中事务失效的8中场景

1. 数据库引擎不支持事务 这里以 MySQL为例&#xff0c;MyISAM引擎是不支持事务操作的&#xff0c;一般要支持事务都会使用InnoDB引擎&#xff0c;根据MySQL 的官方文档说明&#xff0c;从MySQL 5.5.5 开始的默认存储引擎是 InnoDB&#xff0c;之前默认的都是 MyISAM&#xff…
阅读更多...
【node】使用express+gitee搭建图床，并解决防盗链问题

【node】使用express+gitee搭建图床，并解决防盗链问题

首先创建一个gitee的项目&#xff0c;详细步骤我就不一一说明 注解&#xff1a;大家记得将这个项目开源&#xff0c;还有记得获取自己的私钥&#xff0c;私钥操作如下&#xff1a; node依赖下载&#xff1a; "axios": "cors": "express"…
阅读更多...
FPGA设计时序分析一、时序路径

FPGA设计时序分析一、时序路径

目录 一、前言 二、时序路径 2.1 时序路径构成 2.2 时序路径分类 2.3 数据捕获 2.4 Fast corner/Slow corner 2.5 Vivado时序报告 三、参考资料 一、前言 时序路径字面容易简单地理解为时钟路径&#xff0c;事实时钟存在的意义是为了数据的处理、传输&#xff0c;因此严…
阅读更多...
记一次简单的MySql注入试验

记一次简单的MySql注入试验

试验环境&#xff1a; 1.已经搭建好的php服务器&#xff0c;并可以通过访问到localhost/index.php&#xff1b; 2.已经安装好数据库&#xff0c;并创建表test&#xff0c;表内有name、age等字段&#xff0c;并随便创建几个假数据用于测试&#xff1b;如图&#xff1a; 开始测…
阅读更多...
docker 禅道 远程链接 MySQL

docker 禅道 远程链接 MySQL

主要的坑在下边 红色字体&#xff1a;认真看 第一种方法 搜索镜像 docker search zentao 拉取镜像 docker pull easysoft/zentao:latest 启动容器 –name [容器名] 设置容器名称 -p [主机端口]:80 绑定端口 -v /home/zentao/zentaopms:/www/zentaopms 挂载数据目录 /h…
阅读更多...
idea中Easy Code模版配置

idea中Easy Code模版配置

首先找到模版位置 找到使用的模版&#xff0c;我用的是MybatisPlus-H,这是我新建的一个模版 controller.java.vm模版 ##导入宏定义 $!{define.vm}##设置表后缀&#xff08;宏定义&#xff09; #setTableSuffix("Controller")##保存文件&#xff08;宏定义&#xff…
阅读更多...
PHP8知识详解：PHP8开发工具VS Code的安装

PHP8知识详解：PHP8开发工具VS Code的安装

作为PHP8的开发工具有很多&#xff0c;具有IDE功能的有phpstorm、Visual Studio Code、Sublime Text、NetBeans、Eclipse、Codelobster、PHP Designer等&#xff0c;当然还有很多轻量的工具&#xff0c;比如Notepad、Editplus等。本文给你介绍的是万能编辑器Visual Studio Code…
阅读更多...
Python基于PyTorch实现循环神经网络回归模型(LSTM回归算法)项目实战

Python基于PyTorch实现循环神经网络回归模型(LSTM回归算法)项目实战

说明&#xff1a;这是一个机器学习实战项目&#xff08;附带数据代码文档视频讲解&#xff09;&#xff0c;如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 LSTM网络是目前更加通用的循环神经网络结构&#xff0c;全称为Long Short-Term Memory&#xff0c;翻…
阅读更多...
计算机视觉（二）图像特征提取

计算机视觉（二）图像特征提取

文章目录 颜色特征量化颜色直方图适用颜色空间&#xff1a;RGB、HSV等颜色空间操作 几何特征边缘 Edge边缘定义边缘提取 基于关键点的特征描述子引入几何特征&#xff1a;关键点几何特征&#xff1a;Harris角点FAST角点检测几何特征&#xff1a;斑点局部特征&#xff1a;SIFT预…
阅读更多...
GPT-4 模型详细教程

GPT-4 模型详细教程

GPT-4&#xff08;Generative Pretrained Transformer 4&#xff09;是 OpenAI 的最新语言生成模型&#xff0c;其在各类文本生成任务中表现优秀&#xff0c;深受开发者和研究者喜爱。这篇教程将帮助你理解 GPT-4 的基本概念&#xff0c;并向你展示如何使用它来生成文本。 什么…
阅读更多...
前端vue入门(纯代码)35_导航守卫

前端vue入门(纯代码)35_导航守卫

星光不问赶路人&#xff0c;时光不负有心人 【33.Vue Router--导航守卫】 导航守卫 正如其名&#xff0c;vue-router 提供的导航守卫主要用来通过跳转或取消的方式守卫导航。有多种机会植入路由导航过程中&#xff1a;全局的, 单个路由独享的, 或者组件级的。 记住参数或查…
阅读更多...
uniapp JS文件里面调用自定义组件（不用每个页面在template中加组件标签）

uniapp JS文件里面调用自定义组件（不用每个页面在template中加组件标签）

前言 工具&#xff1a;uniapp 开发端&#xff1a;微信小程序 其他&#xff1a;uview 2.0 场景&#xff1a;路由器里面&#xff0c;统一验证是否已登录&#xff0c;如果没登录&#xff0c;则直接弹出登录弹窗出来&#xff0c;不管哪个页面都如此。 效果如下&#xff1a; 直接上…
阅读更多...
【笔试强训选择题】Day29.习题（错题）解析

【笔试强训选择题】Day29.习题（错题）解析

作者简介&#xff1a;大家好&#xff0c;我是未央&#xff1b; 博客首页&#xff1a;未央.303 系列专栏&#xff1a;笔试强训选择题 每日一句&#xff1a;人的一生&#xff0c;可以有所作为的时机只有一次&#xff0c;那就是现在&#xff01;&#xff01;&#xff01;&#xff…
阅读更多...
「2024」预备研究生mem-复习-倒数形态乘法公式

「2024」预备研究生mem-复习-倒数形态乘法公式

一、倒数形态乘法公式-完全平方
阅读更多...
rsync—远程同步

rsync—远程同步

目录 一&#xff1a;rsync概述 1.1rsync简介 1.2rsync同步方式 二&#xff1a;rsync特性 三&#xff1a;rsync同步源 四&#xff1a;rsync与cp、scp对比 五&#xff1a;常用rsync命令 六&#xff1a;rsync本地复制实例 七&#xff1a;配置源的俩种表示方法 八&#x…
阅读更多...
[NLP]Huggingface模型/数据文件下载方法

[NLP]Huggingface模型/数据文件下载方法

问题描述 作为一名自然语言处理算法人员&#xff0c;hugging face开源的transformers包在日常的使用十分频繁。在使用过程中&#xff0c;每次使用新模型的时候都需要进行下载。如果训练用的服务器有网&#xff0c;那么可以通过调用from_pretrained方法直接下载模型。但是就本人…
阅读更多...
安全DNS，状态码，编码笔记整理

安全DNS，状态码，编码笔记整理

一 DNS DNS&#xff08;Domain Name System&#xff09;是互联网中用于将域名转换为IP地址的系统。 DNS的主要功能包括以下几个方面&#xff1a; 域名解析&#xff1a;DNS最主要的功能是将用户输入的域名解析为对应的IP地址。当用户在浏览器中输入一个域名时&#xff0c;操作…
阅读更多...
工程安全监测无线振弦采集仪在建筑物中的应用

工程安全监测无线振弦采集仪在建筑物中的应用

工程安全监测无线振弦采集仪在建筑物中的应用 工程安全监测无线振弦采集仪是一种用于建筑物结构安全监测的设备&#xff0c;它采用了无线传输技术&#xff0c;具有实时性强、数据精度高等优点&#xff0c;被广泛应用于建筑物结构的实时监测和预警。下面将从设备的特点、应用场…
阅读更多...
力扣热门100题之接雨水【困难】

力扣热门100题之接雨水【困难】

题目描述 给定 n 个非负整数表示每个宽度为 1 的柱子的高度图&#xff0c;计算按此排列的柱子&#xff0c;下雨之后能接多少雨水。 示例 1&#xff1a; 输入&#xff1a;height [0,1,0,2,1,0,1,3,2,1,2,1] 输出&#xff1a;6 解释&#xff1a;上面是由数组 [0,1,0,2,1,0,1,3…
阅读更多...
如何使用GPT作为SQL查询引擎的自然语言

如何使用GPT作为SQL查询引擎的自然语言

​生成的AI输出并不总是可靠的&#xff0c;但是下面我会讲述如何改进你的代码和查询的方法&#xff0c;以及防止发送敏感数据的方法。与大多数生成式AI一样&#xff0c;OpenAI的API的结果仍然不完美&#xff0c;这意味着我们不能完全信任它们。幸运的是&#xff0c;现在我们可以…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023