本文章学习研究PID闭环回路控制算法，介绍帮助大家理解这个算法，希望看后觉得有用就三连支持一下。

目录

认识PID:

PID算法知识理论学习：

 首先看PID原理的框图：

一、比例算法P：

二、积分算法I：

三、微分算法D：

---

 

认识PID:

PID算法的应用领域：

PID算法主要运用在自动控制系统中，常见的领域包括工业控制、机器人控制、航空航天、汽车控制、水处理、温度控制、流量控制等。

PID算法可以根据系统的反馈信号来实时调整控制参数，使系统的输出能够快速稳定地达到预期值。通过PID算法的应用，可以提高系统的稳定性、精度和响应速度，从而实现自动控制。

PID算法的输入一般就俩个：是当前反馈传感器的值与用户设定值，然后根据俩者的误差，直接计算出其期望功率，从而加快或减少电机转速.

PID算法知识理论学习：

 首先看PID原理的框图：

从这个图中我们了解到，整个计算过程其实是对于“误差”，来进行一系列计算的，输入也只要有设定值Sv与反馈值Pv,它的输出计算是根据历史、当前、趋势来进行计算的，参照传感器数据达标与否，用户设定值与其误差为多少，来进行输出上的自动调整，整个流程从而形成回路

现在我们通过传感器采样从开机以来所有采样点的数据序列（理论上时间间隔越短越好）

X1、X2、... 、Xn-1、Xn ,然后从这三方面挖掘PID的三个算法原理：

 

以下是网上找的图，可以对照看看：

其中R(t)是设定，U（t）是输出，C（t）是传感器反馈

 

一、比例算法P：

公式：Pout=Kp*Ek  其中（ Ek=Sv-Xk ）

Ek是误差的意思，Sv是用户设定值，Xk是传感器传回的数据，Kp是一个比例，是需要根据实际情况进行调整的。

 

原理：

这个算法是直接根据误差来进行比例上的计算，将误差乘以比例，直接输出，误差有三种情况：

Ek>0:当前未达标、Ek=0：正好达标、Ek<0:当前超标。根据这三种情况，比例性地放大、缩小偏差值。

系统上会控制输出更快速得接近目标值

单独使用的缺点：

因为Pout=Kp*Ek  ，所以 Ek=0：正好达标时，输出也为0，有误差才起左右，没误差就不动了。

系统上体现单独使用容易产生震荡：

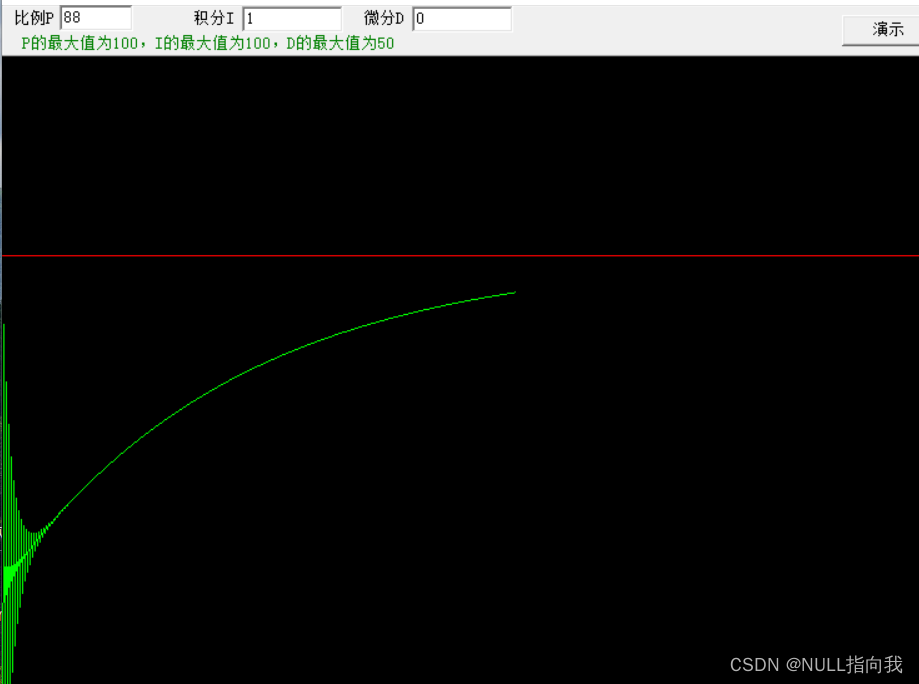
下图为震荡的演示：

比例过大导致起初有许多超调，这个图的演示其实不太准确，但大致表现出单独的比例算法对于物理惯性的稳定方面有所劣势：

 

二、积分算法I：

 公式：Iout=Ki*Sk  其中（ Sk=E1+E2+...+Ek-1+Ek ）

 Sk是指开机以来的偏差的相加的值，Ki是积分的比例，是需要根据实际情况进行调整的。

 

原理：

这个算法累加过去的误差，根据历史值来计算输出。过去总体未达标：给增强信号，过去整体超标：给减弱信号，累计误差有三种情况：

 Sk>0:过去整体不达标， Sk=0：过去整体达标， Sk<0：过去整体超标

系统上会累计减小误差

单独使用的缺点：

Sk=0，就会无输出

过多的累计历史误差，会有历史遗留问题，有些历史误差是不需要过多被累计的

三、微分算法D：

 公式：Dout=Kd*Dk  其中（ Dk=Ek-Ek-1 ）

Dk是指最近俩次偏差值的相减，预示着一种趋势

原理：

微分考虑最近的俩次偏差值，获取一种趋势;

Dk>0:上升趋势，Dk=0:不变趋势，Dk<0:下降趋势

系统上，D算法可以抵消P算法单独使用带来的计算溢出，但调整不当会有反冲现象：

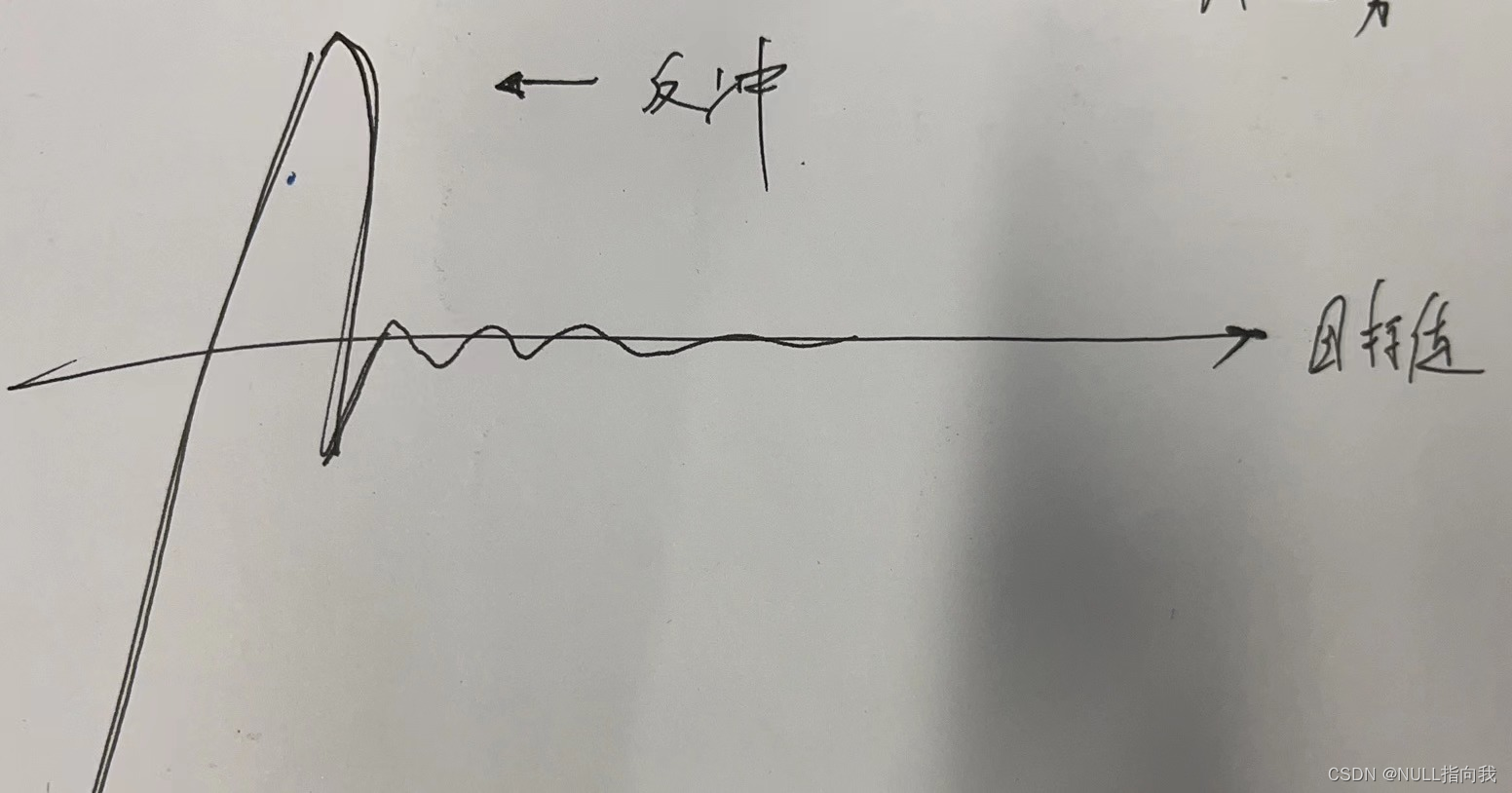
 下图为反冲的演示：

D算法占比过大，大致演示反冲，图不准确，但大致是这意思~

 

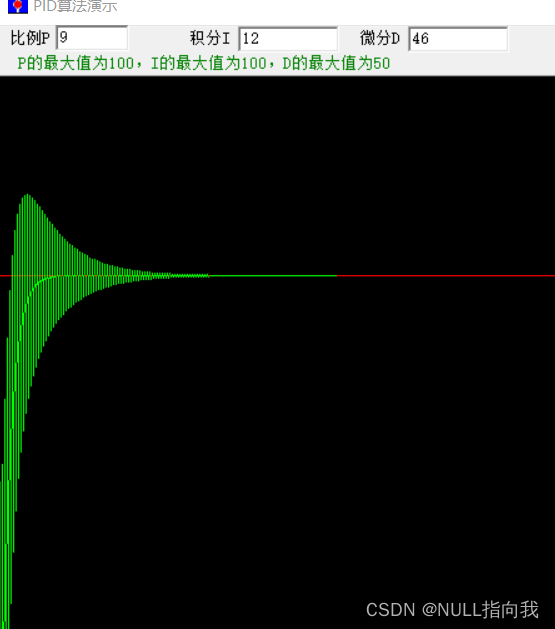
单独使用的缺点：

 这个没法单独使用

调整PID有关思路：