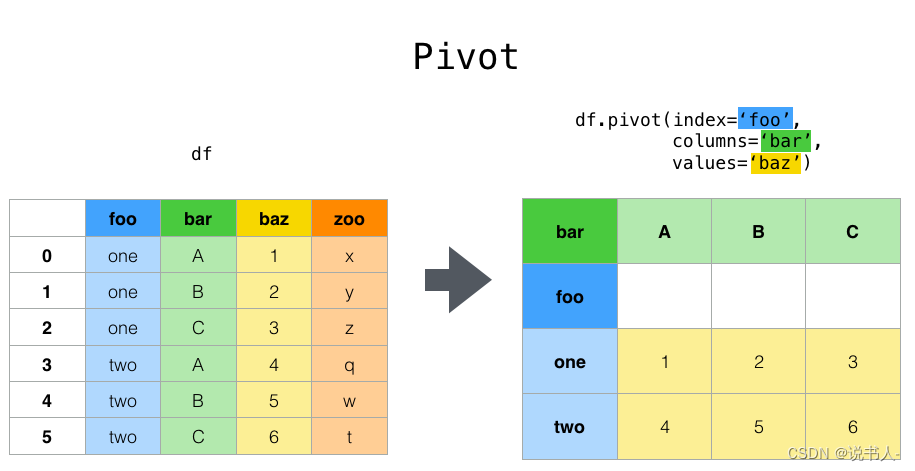
A 按分隔符拆分字符串

简单模拟
class Solution {
public:
vector<string> splitWordsBySeparator(vector<string> &words, char separator) {
vector<string> res;
for (auto &s: words) {
int n = s.size();
for (int i = 0, j = 0; i < n;) {
while (j < n && s[j] != separator)
j++;
if (i < j)
res.push_back(s.substr(i, j - i));
i = j + 1;
j = i;
}
}
return res;
}
};
B 合并后数组中的最大元素
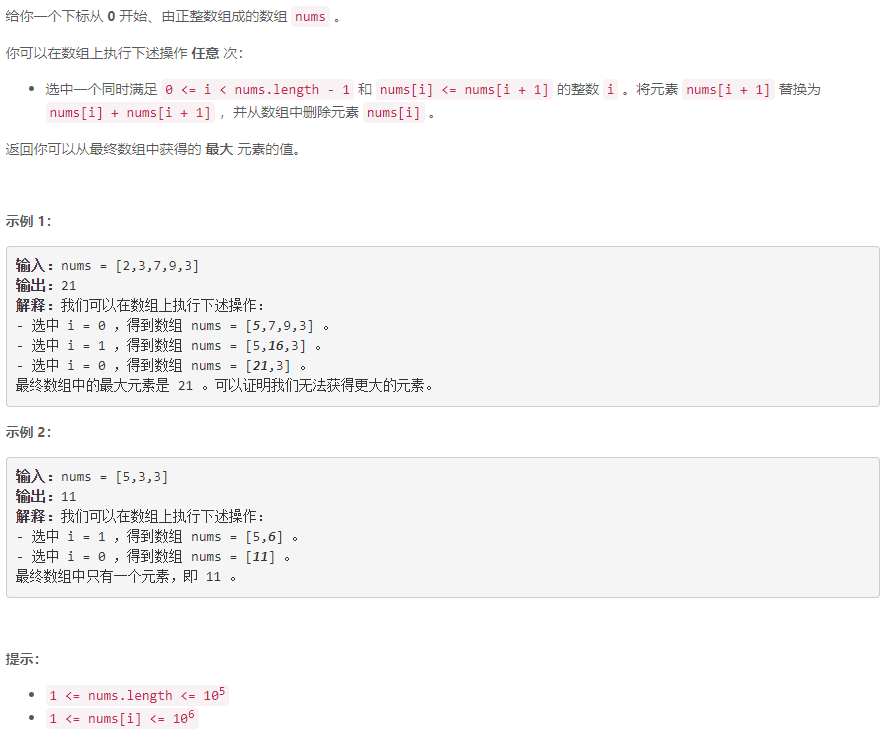
倒序遍历数组, 计算当前最右元素可以合并生成的最大元素
class Solution {
public:
typedef long long ll;
long long maxArrayValue(vector<int> &nums) {
int n = nums.size();
ll cur = nums[n - 1];//生成的当前元素
ll res = nums[n - 1];
for (int i = n - 2; i >= 0; i--) {
if (nums[i] <= cur) {
cur += nums[i];
} else {//以nums[i]为新的最右元素
cur = nums[i];
}
res = max(res, cur);
}
return res;
}
};
C 长度递增组的最大数目
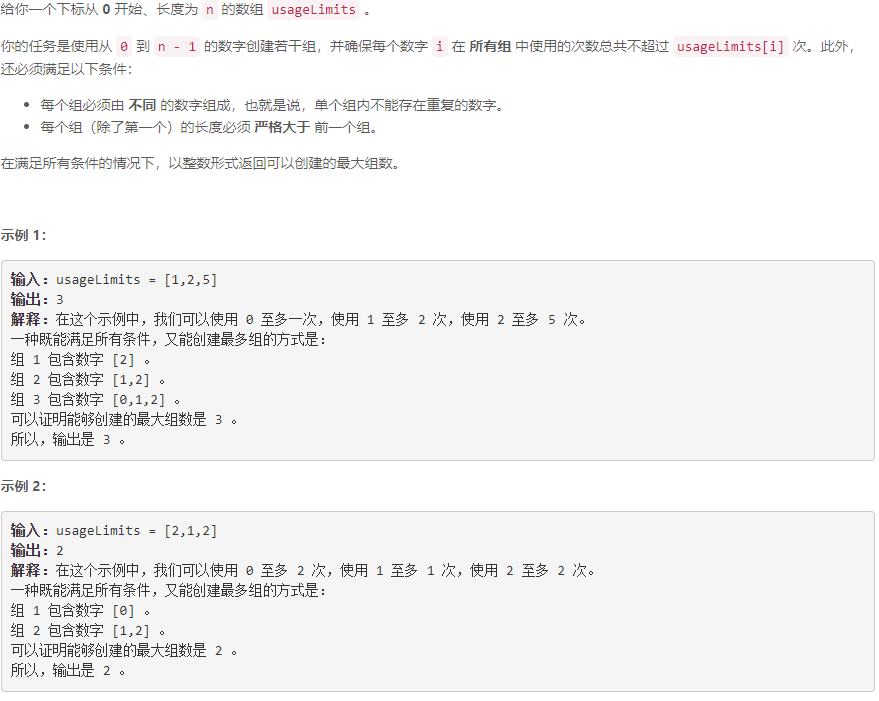
先放个赛事凑出来的二分占位(不知道会不会被rejudge),后续看看能不能补个证明或贴个其他方法…
class Solution {
public:
typedef long long ll;
int maxIncreasingGroups(vector<int> &usageLimits) {
sort(usageLimits.begin(), usageLimits.end(), greater<>());
int n = usageLimits.size();
int l = 1, r = n;
while (l < r) {
int mid = (l + r + 1) / 2;
ll cur = 0;
for (int i = 0; i < n; i++) {
if (i + 1 <= mid)
cur = min(1LL * (i + 1) * (mid * 2 - i) / 2, cur + usageLimits[i]);
else
cur += usageLimits[i];
}
if (cur >= 1LL * mid * (mid + 1) / 2)
l = mid;
else
r = mid - 1;
}
return l;
}
};
D 树中可以形成回文的路径数

dfs+计数: 设 u , v u,v u,v两点之间路径上各字符数量的奇偶组成状态为 m a s k mask mask, u u u和根节点之间路径上各字符数量的奇偶组成状态为 m a s k u mask_u masku, v v v和根节点之间路径上各字符数量的奇偶组成状态为 m a s k v mask_v maskv, 则有 m a s k = m a s k u ∧ m a s k v mask=mask_u\wedge mask_v mask=masku∧maskv. 设 u , v u,v u,v两点之间路径上各字符重排可以构成回文, 则 m a s k mask mask二进制表示最多有一位为1. 通过 d f s dfs dfs用哈希记录各点与根节点路径的字符奇偶状态 m a s k k mask_k maskk, 然后枚举哈希中的 m a s k i mask_i maski计算.
class Solution {
public:
long long countPalindromePaths(vector<int> &parent, string s) {
int n = parent.size();
vector<pair<int, char>> sub[n];//邻接表
for (int i = 1; i < n; i++)//建树
sub[parent[i]].emplace_back(i, s[i]);
unordered_map<int, int> cnt;//记录状态出现次数
function<void(int, int)> dfs = [&](int cur, int mask) {
cnt[mask]++;
for (auto [j, ch]: sub[cur])
dfs(j, mask ^ (1 << (ch - 'a')));
};
dfs(0, 0);
long long res = 0;
for (auto [mi, ci]: cnt) {
if (ci > 1)//状态相同的情况
res += 1LL * ci * (ci - 1);
for (int j = 1; j < (1 << 26); j <<= 1)//枚举二进制只差一位的状态
if (cnt.count(mi ^ j))
res += 1LL * ci * cnt[mi ^ j];
}
return res / 2;
}
};