目录

2.数据的表示和运算

2.3浮点数的表示与运算

2.3部分习题 

---

2.数据的表示和运算

2.3浮点数的表示与运算

---

2.3部分习题 

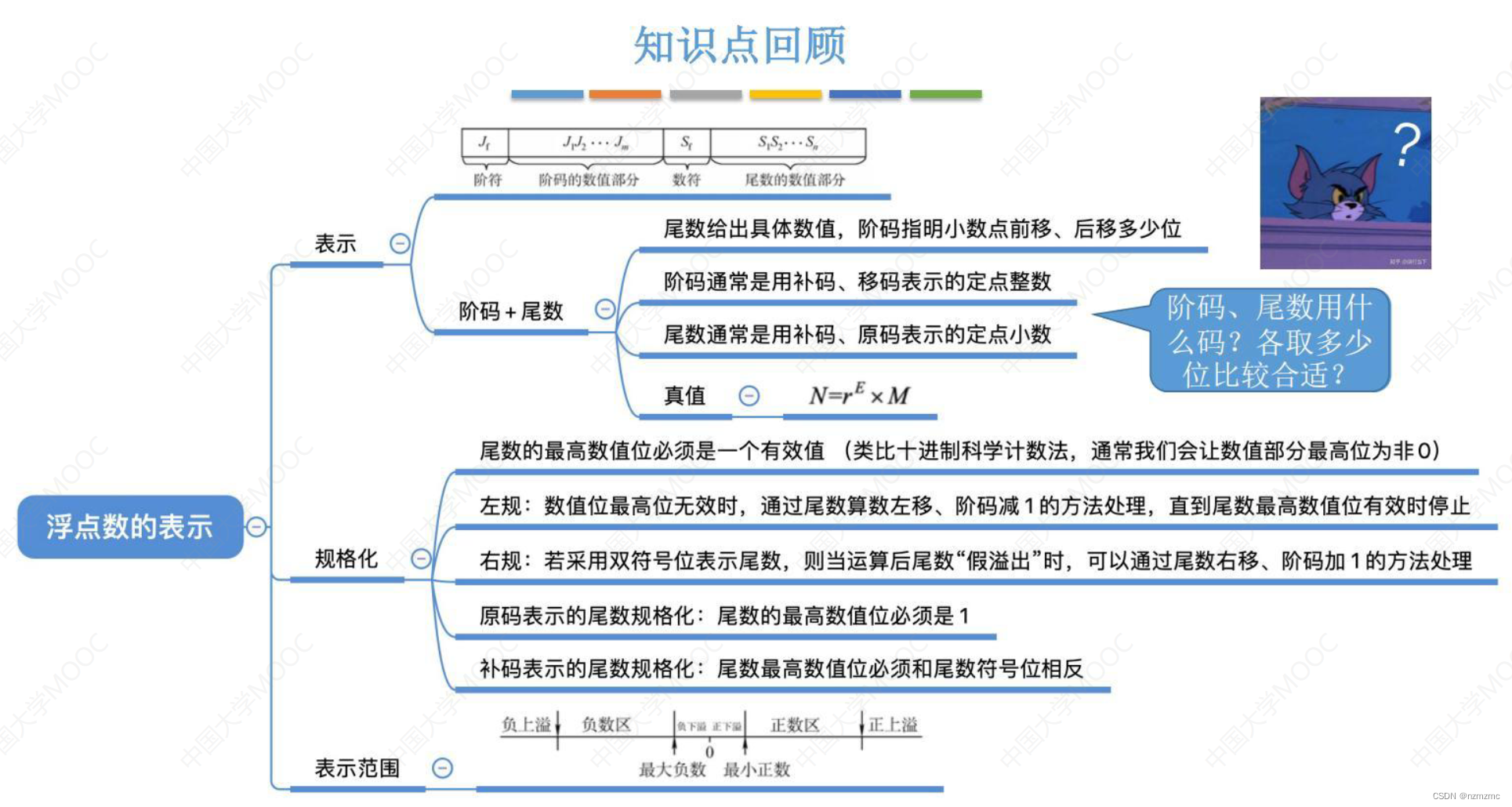
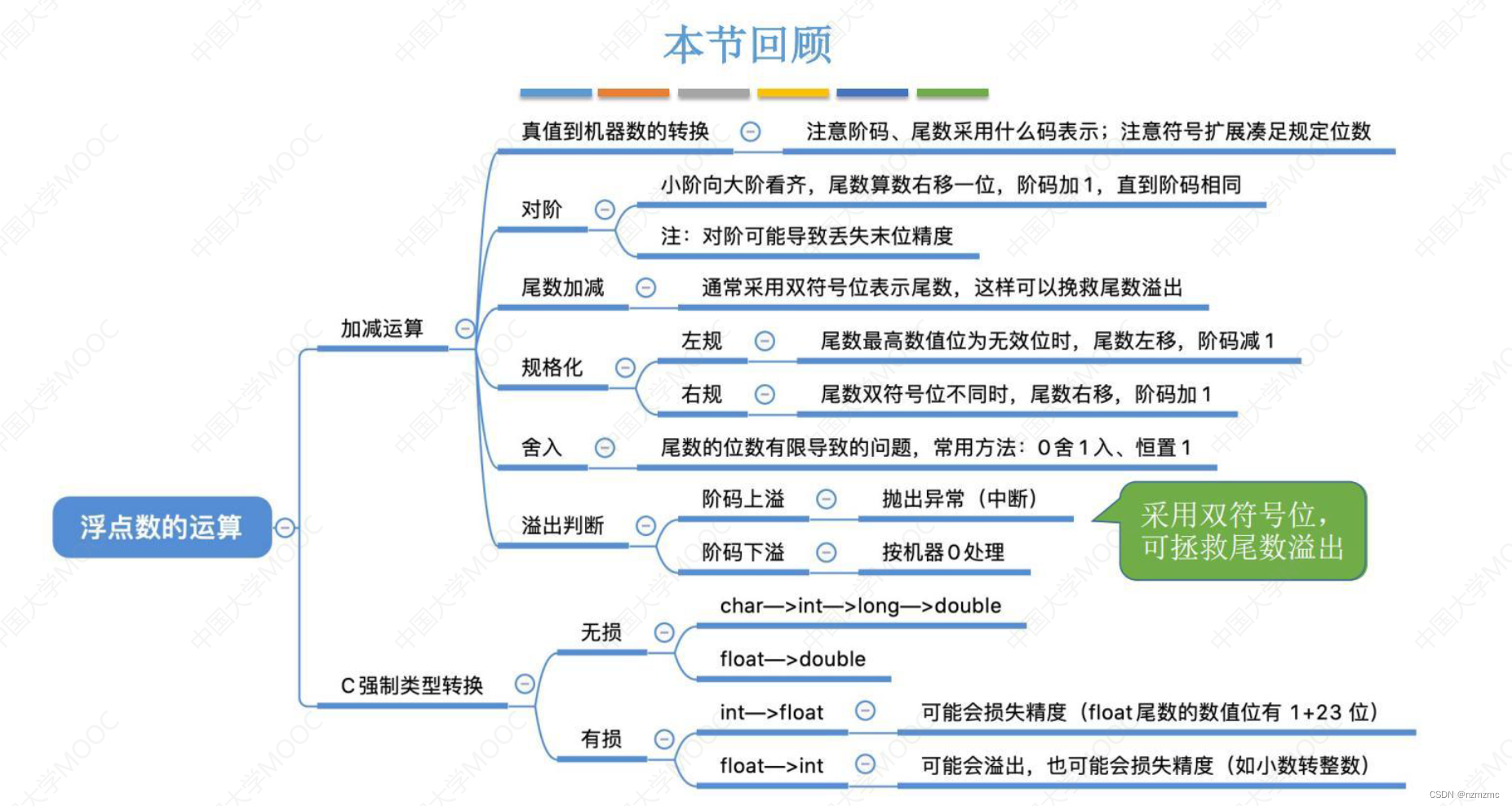
1.下列关于对阶操作，正确的是（）

A.在浮点加减运算的对阶操作中，若阶码减小，则尾数左移

B.在浮点加减运算的对阶操作中，若阶码增大，则尾数右移；若阶码减小，则尾数左移

C.在浮点加减运算的对阶操作中，若阶码增大，则尾数右移

D.以上都不对

2.在IEEE 754标准规定的64位浮点数格式中，符号位为1位，阶码为11位，尾数为52位，则它所能表示的最小规格化负数为（）

A.

B.

C.

D.

3.设浮点数共12位，其中阶码含1位阶符共4位，以2为底，补码表示；尾数含1位数符共8位，补码表示，规格化。则该浮点数所能表示的最大正数是（）

A.        B.        C.        D.

4.设浮点数的阶码和尾数均采用补码表示，且位数分别为5和7（均含2位符号位），若有两个数X=和Y=，则用浮点加法计算X+Y的最终结果是（）

A.00111 1100010        B.00111 0100010        

C.01000 0010001        D.发生溢出

5.float类型（IEEE754单精度浮点数格式）能表示的最大正整数是（）

A.        B.        C.        D.

6.已知带符号整数用补码表示，float型数据用IEEE754标准表示，假定变量x的类型只可能是int或float，当x的机器数为C800 000H时，x的值可能是（）

A.        B.        C.        D.

7.-0.4375的IEEE754单精度浮点数表示为（）

A.BEE0 0000H        B.BF60 0000H        C.BF70 0000H        D.C0E0 000H

---

1.C

对阶操作是将较小的阶码调整到与较大的阶码一致，因此不存在阶码减小，位数左移

2.B

长浮点数，阶码11位，尾数52位，采取隐藏位策略，因此其最小规格化负数为阶码取最大值，尾数最大值，符号位为负

3.D

使浮点数最大，使尾数取正数最大，阶码取正数最大，尾数为8位补码（含符号位），最大0.1111111，即，阶码4位，最大0111，即7，则最大正数（）*=

4.D

X的浮点数格式为00，111；00，11101（分号前为阶码，后为尾数），Y的浮点数格式为00，101；00，10100

1.对阶：X、Y阶码相减，小阶向大阶看齐，将Y的阶码加2，尾数右移2位，Y变为00，111；00，00101

2.尾数相加：结果符号位为01，需要右规

3.规格化：将尾数右移1位，阶码加1，得X+Y为01，000；00，10001

4.判断溢出：阶码符号位为01，说明发生溢出

5.D

一位符号位，阶码E取值1~254（8位），尾数m23位，共32位，最大整数1.111~1*=

6.A

C800 000H=1100 1000 0000 0000 0000 0000 0000 0000

转为float和int型：

float型：尾数隐藏最高位1，阶码1001 0000==128+16，减去偏置值127，x为

int型：带符号补码，为负，得011 1000 0000 0000 0000 0000 0000 0000算出x为

7.A

-0.4375=-1.75*，数符为1，阶码为-2+127=125，即01111101，隐藏小数点前得“1”，0.75写成二进制0.11，所以尾数部分为1100~0，二进制对应为1011 1110 1110 0000 0000 0000 0000 0000，对应十六进制为BEE0 000H