Overviews

What problem is addressed in the paper?

We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics.

What is the key to the solution?

Our best results are obtained by training on a weighted variational bound designed according to a novel connection between diffusion probabilistic models and denoising score matching with Langevin dynamics, and our models naturally admit a progressive lossy decompression scheme that can be interpreted as a generalization of autoregressive decoding.

What is the main contribution?

we show that a certain parameterization of diffusion models reveals an equivalence with denoising score matching over multiple noise levels during training and with annealed Langevin dynamics during sampling (Section 3.2) [ 55, 61 ]. We obtained our best sample quality results using this parameterization (Section 4.2), so we consider this equivalence to be one of our primary contributions.

Contents

扩散概率模型

扩散概率模型(为方便起见，我们将其称为“扩散模型”)是一种参数化的马尔可夫链，使用变分推理训练产生有限时间后与数据匹配的样本。学习该链的跃迁来逆转扩散过程，这是一个马尔可夫链，逐步向采样的相反方向的数据添加噪声，直到信号被破坏。当扩散由少量高斯噪声组成时，将采样链跃迁设置为条件高斯也就足够了，允许特别简单的神经网络参数化。

扩散模型的定义很简单，训练起来也很有效，但据我们所知，还没有证据表明它们能够生成高质量的样本。我们证明了扩散模型实际上能够生成高质量的样本，有时比其他类型生成模型发表的结果更好(第4节)。此外，我们还表明，扩散模型的某个参数化揭示了在训练过程中与在多个噪声水平上去噪得分匹配以及在采样过程中与退火朗之万动力学等价(第3.2节)[55,61]。我们使用这个参数化(第4.2节)获得了最好的样本质量结果，因此我们认为这种等价性是我们的主要贡献之一。

我们发现，我们的模型的大部分无损编码长度被用于描述难以察觉的图像细节(第4.3节)。我们用有损压缩的语言对这一现象进行了更精细的分析，并表明扩散模型的采样过程是一种渐进式解码，它类似于自回归解码，沿着比特排序，极大地推广了自回归模型通常可能的内容。

背景

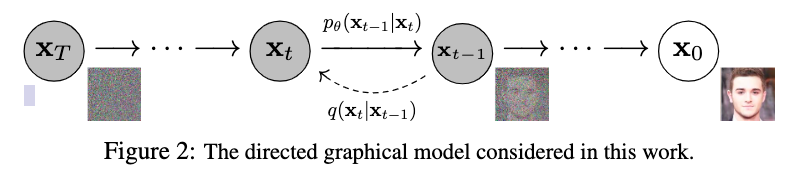
扩散模型是一种潜变量模型，用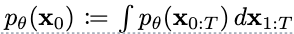表示，其中联合分布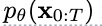叫做reverse process，它被定义为具有学习高斯跃迁的马尔可夫链。

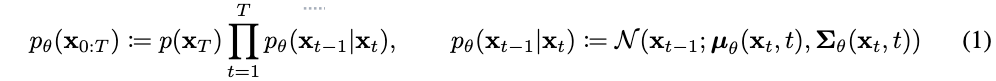
扩散模型与其他潜在变量模型的区别在于近似后验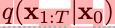（也叫做forward process or diffusion process）被固定到一个马尔可夫链上，根据方差表逐步向数据添加高斯噪声。

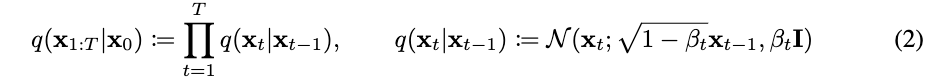
训练是通过优化通常的负对数似然的变分界来进行的：

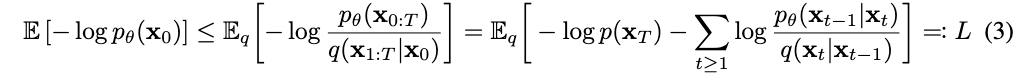
如果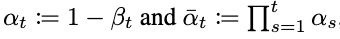，则：

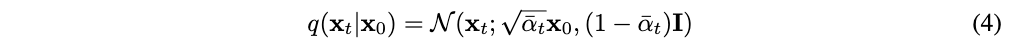
因此，公式3可以改写为：

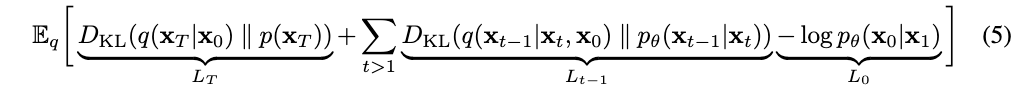
当条件为x0时：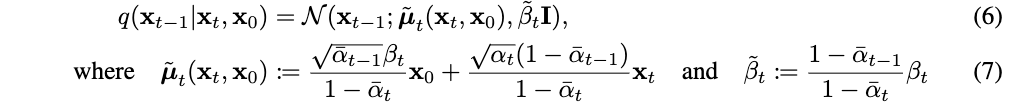

算法

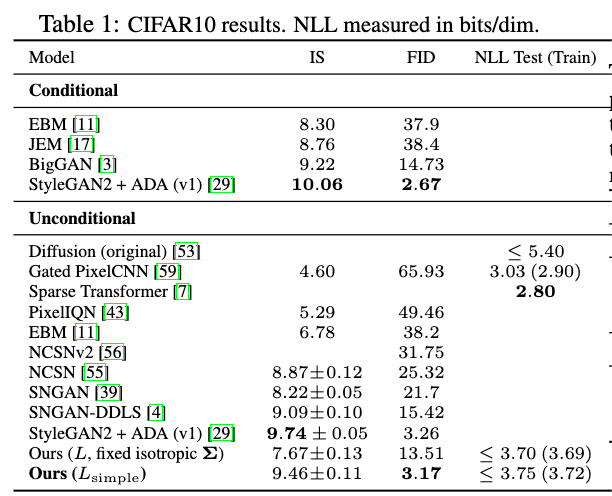
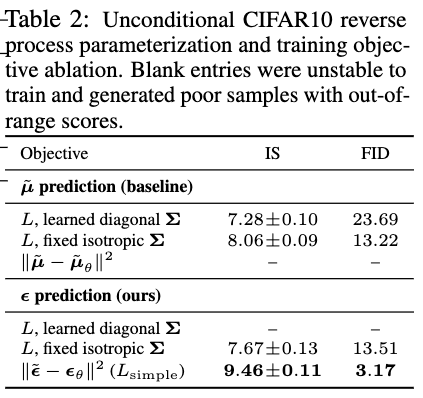
实验

结论

我们使用扩散模型展示了高质量的图像样本，并且我们发现了用于训练马尔可夫链的扩散模型和变分推断之间的联系，去噪分数匹配和退火朗之万动力学(以及扩展后的基于能量的模型)，自回归模型和渐进有损压缩。由于扩散模型似乎对图像数据有优秀的归纳偏见，我们期待着研究它们在其他数据模式中的效用，以及作为其他类型的生成模型和机器学习系统的组成部分。