特征工程

把特征转换为机器容易识别的数据，把特征a转化为机器容易读懂、量化的语言

归一化Min-Max

将原始数据映射到[0,1]之间
$$X^{\prime }=\frac{x-min}{max-min}$$
但是归一化是有弊端的，比如有一个值错误，就会影响整体的数值，并且归一化是无法解决这个异常值。所以归一化只适合传统精确小数据场景。

标准化

通过对原始数据进行变换把数据变换到均值为0,标准差为1范围内。也就是服从正态分布的数据。
$$X^{\prime }=\frac{x-mean}{\sigma }$$

K-近邻算法(K-Nearest Neighboor)

定义

如果一个样本在特征空间中的k个最相似(即特征空间中最邻近)的样本中的大多数属于某一个类别，则该样本也属于这个类别。

理念

取近的邻居，本质为近朱者赤近墨者黑，比如可以通过身边的住户预测本区域送外卖的是哪些人。所以就要用欧式距离计算出跟邻居的距离，找出最近的邻居(k=1)。
问题：只有1个的话数据不够精准，被噪点的干扰太强，数据有误差的话就会被完全带偏。
解决：要找k个邻居，自己写代码实现knn。knn算法也可以用于动态加载的字体反爬。

理解K近邻

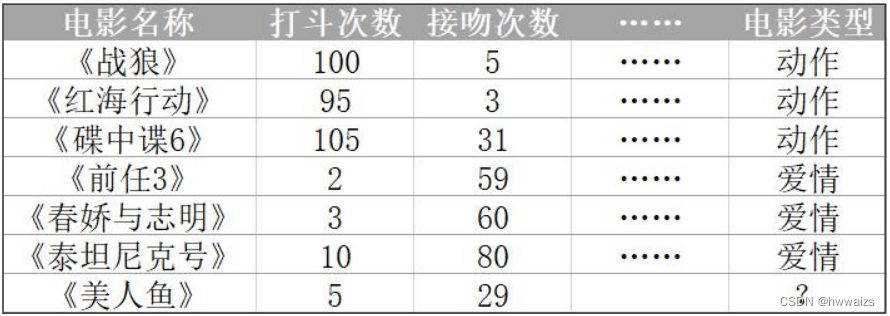
已知《战狼》、《红海行动》、《碟中谍6》是动作片，而《前任3》、《春娇与志明》、《泰坦尼克号》是爱情片。每一行(一部电影)为一个数据样本，特征列为打斗次数、接吻次数，根据打斗次数和接吻次数来区分是爱情片和动作片。如果新的电影如《美人鱼》，人可以根据自己经验将电影进行分类，也可以让机器也可以掌握一个分类的规则，自动的将新电影进行分类。

对图中的数据进行整理，绘制散点图如下：

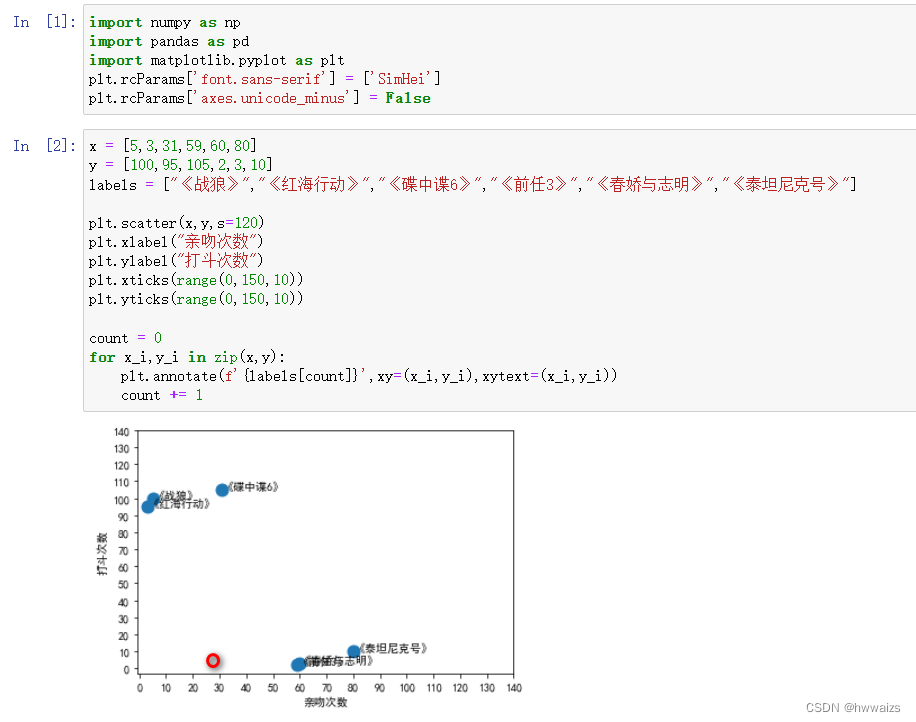
通过分析结果可以看出，动作片的打斗场景非常多，根据《美人鱼》电影的数据，可以大致判断出在图中红色圆圈的位置。现在就要判断出红色圆圈距离哪一个样本点比较近，如果距离《春娇与志明》比较近，就可以归类为爱情片，如果距离《红海行动》比较近的话就可以归类为动作片。
两点之间的直线距离最近。

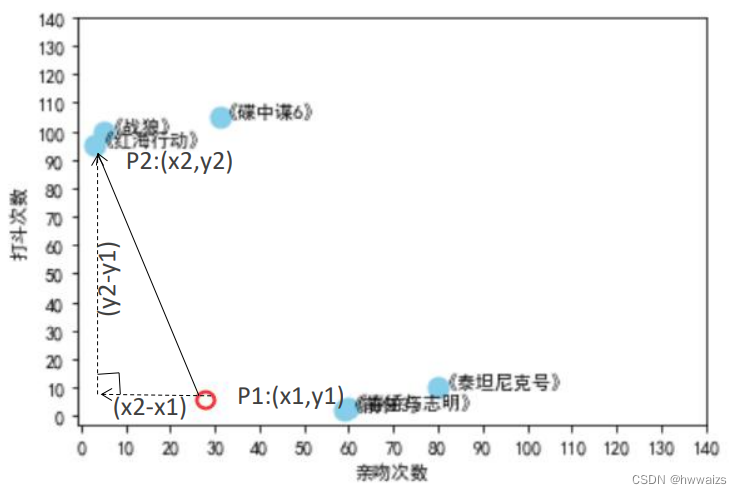
在机器学习中说到两点之间的距离，通常指的是欧式距离，二维欧式距离公式如下：
$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
特征不可能说只有两个，每个特征代表一个维度，同理衍生三维欧氏距离公式如下：
$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2}$$
如果是四维或者更高维度，归纳N维欧式距离公式如下：
$$d_{12}=\sqrt{\sum _{k=1}^n(x_i-y_i{)}^2}$$
对距离进行精准计算，以两点(美人鱼、碟中谍6)为例进行求解，

# 美人鱼：5  29
# 碟中谍6： 105 31
np.sqrt((105-5)**2+(31-29)**2)  # 100.0199980003999

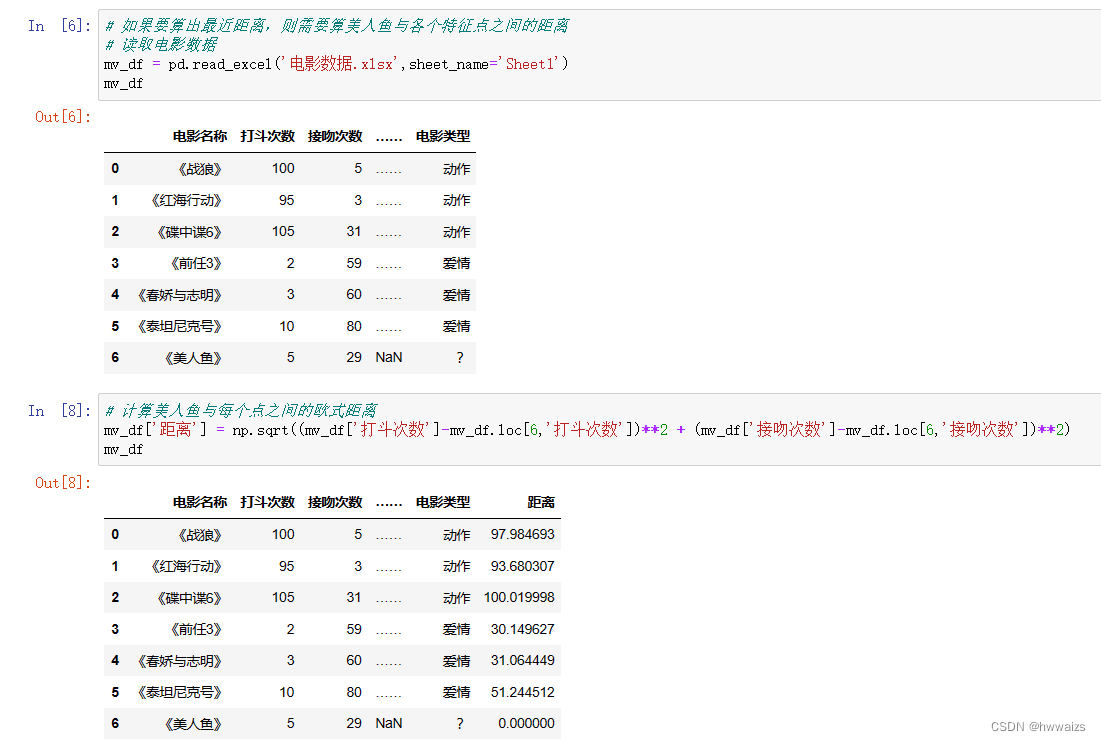
如果要算出最近距离，则需要算《美人鱼》与各个特征点之间的距离。从计算结果可以看出，距离《美人鱼》最近的电影是《前任3》，如果只从一个特征点去判定的话，结果可能会不精确。这时要选择更多(K值)的附近特征值进行比较，如果选择K=3，选择距离最近的3个，选择的特征值为《前任3》、《春娇与志明》、《泰坦尼克号》，这三个都是爱情电影，可以把《美人鱼》归类为爱情电影。如果选择K=4，就会出现3个爱情电影，1个动作电影，此时就选择众数，将数据归类为出现次数最多的特征里。
如果只用一个特征点的距离就判断类型的话是不可靠的，如下图

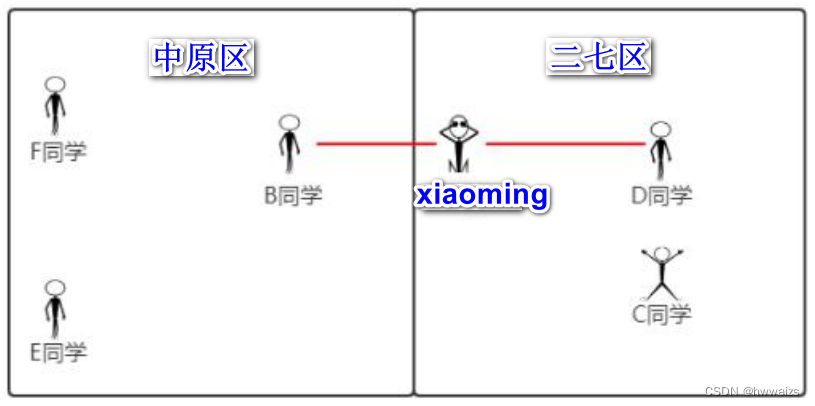
xiaoming其实是在二七区，但是跟B同学的距离最近，这是一个分类的问题，在K近邻算法中，以半径的方式划圈，但是并不能说xiaoming就在中原区，分类问题不能算成均值。如果选择五名同学进行计算，分别计算跟每个同学的距离，要选择类别为众数的，才能更加可靠的来判断出xiaoming所在的区域。xiaoming距离C、D同学最近，E、F同学较远，才能准确的判断xiaoming在哪个区域。

KNN工作流程

• 计算待分类物体与其他物体之间的距离；
• 统计距离最近的 K 个邻居；
• 对于 K 个最近的邻居，它们属于哪个分类最多，待分类物体就属于哪一类。
  基于流程使用numpy和pandas去实现算法。
  
  
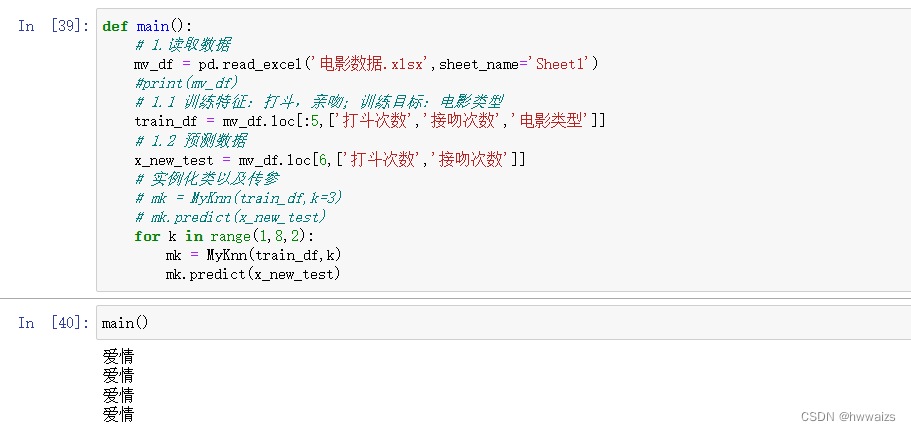
  用编程来实现，就要用到面向对象的编程思想，可以实现动态传参、继承等，避免了函数间的反复接受和调用，实例属性在所有的实例方法立都可以使用。要先封装一个类然后定义一个main()方法，在主程序的方法里进行实例化、调用方法的过程。
  在main()方法里读取数据后，并不能将所有的数据传进去做处理，要把数据划分为初始化的特征，训练特征：打斗次数、亲吻次数；训练目标：电影类型；预测数据；实例化类，传入训练特征、目标数据和K值。
  要把得到的数据传到类中，在类里创建初始化的方法来初始化属性。
  创建预测方法，实现预测《美人鱼》电影属于哪个分类，计算预测数据和真实数据的欧式距离，获取距离最小的前K 个值，对K个点的分类进行统计。此时统计的是当k为确定的值时得到的结果，如果要测试多个，可以进行循环遍历，k最好取奇数。

小结

1. 计算欧式距离
2. 取最近的k个邻居
3. 利用numpy和pandas的广播机制，效率比python的循环要高
4. 选择数据。
   • 1. df.loc[行标签,列标签]，通过标签选择数据
   • 2.df.iloc[行下表,列下标]，通过下标/索引选择数据
5. 1个邻居不可靠，需要选择多个邻居，求的是类别，不是均值。

K-近邻算法api介绍

scikit-learn工具介绍

scikit-learn是基于python语言的机器学习工具。参考说明文档：http://scikitlearn.com.cn

• Python语言是简单高效的数据挖掘和数据分析工具
• Scikit-learn包括许多知名的机器学习算法的实现
• Scikit-learn文档完善，容易上手，有丰富的API

scikit-learn的安装

pip3 install scikit-learn

注意：安装scikit-learn，需要提前安装numpy，Scipy等库

scikit-learn实现K近邻算法–分类问题

从sklearn包下的neighbors模块，调用所用到的KNeighborsClassifier分类器，n_neighbors为指定的K值，

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights='uniform', algorithm='auto')
n_neighbors：查询默认使用的邻居数（默认为 5） 
weights：默认为 “uniform” 表示为每个近邻分配同一权重；
可指定为 “distance” 表示分配权重与查询点的距离成反比；同时还可以自定义权重。

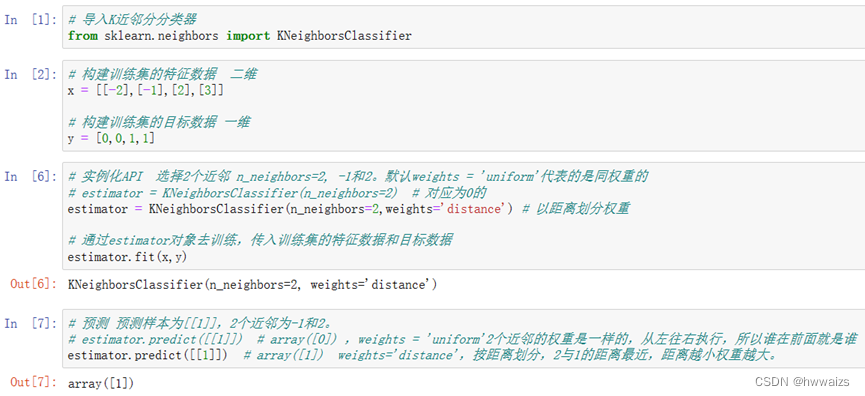
从题目中看到1-，-2是同类别的，为0类别；2，3为同类别的，为1类别。传入的1特征，选择了2个近邻，不仅会找到跟1最近的2，还会找到跟1次近的-1，此时-1和2是同权重的，根据现有的特征数据和结果去训练模型，按距离近的用 weights=‘distance’ 增加权重。

实现电影分类的案例

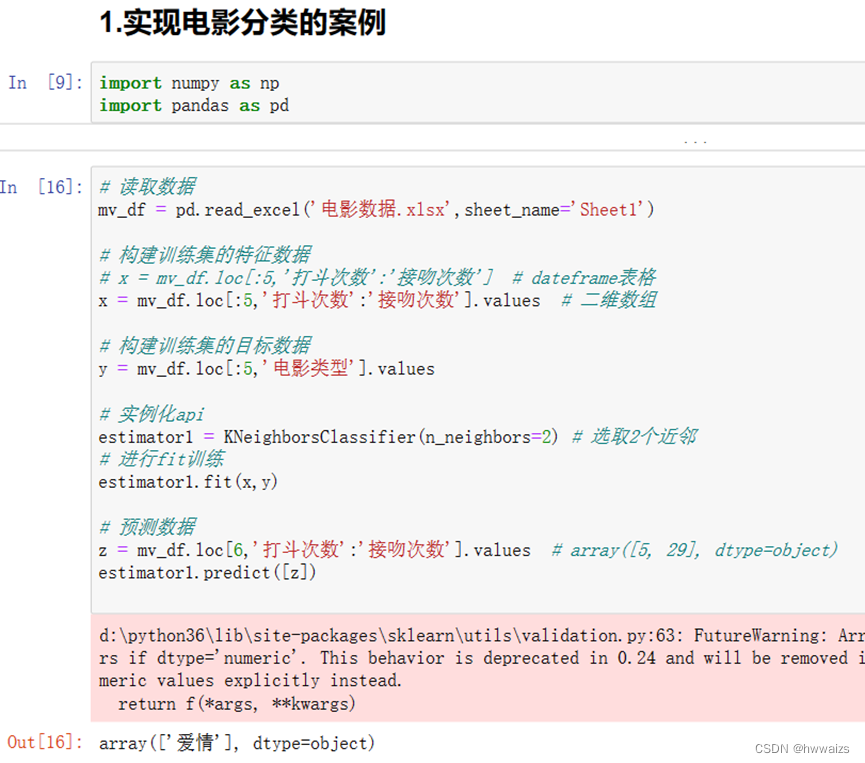
scikit-learn实现K近邻算法–总结

• 构建特征数据与目标数据
• 构建k个近邻的分类器(两个参数：n_neighbors，weights)
• 使用fit进行训练
• 预测数据

K值选择

如果 K 值比较小就相当于未分类物体与它的邻居非常接近才行。这样产生的一个问题就是，如果邻居点是个噪声点，那么未分类物体的分类也会产生误差，这样 KNN 分类就会产生过拟合。通过输入的数据去预测类别，输入的数据要与训练的实例接近才会有结果，如果只取了一个实例(k的取值过小)，好比每天只练习一种题型，考试的时候遇到复杂的题型就会不知所措，只会记住自己训练出来的模板，对一种题型训练过度，就出现过拟合的现象。
如果 K 值比较大，相当于距离过远的点也会对未知物体的分类产生影响，虽然这种情况的好处是鲁棒性强，但是不足也很明显，会受到样本均衡的影响，产生欠拟合情况，也就是没有把未分类物体真正分类出来。k值过大，抗风险能力比较强，好比备考的时候，什么题型都看(海纳百川)，那任何一部电影传进来，都会见过类似的。考试的知识点是初中的，备考的时候复习了小学、初中、高中、大学的内容，考试的时候就不知道用初中、高中、还是大学的知识去解题(都接触过，又都不那么深入)，分不清对应的考点，就会有欠拟合的现象。
用N个K值从小到大进行测试，选择结果最好的那个K值，人为的一个一个的测试会很繁琐，可以用交叉验证。交叉验证的思路就是，把样本集中的大部分样本作为训练集，剩余的小部分样本用于预测，来验证分类模型的准确性。所以在 KNN 算法中，我们一般会把 K 值选取在较小的范围内，同时在验证集上准确率最高的那一个最终确定作为 K 值。

距离计算

• 欧氏距离(欧几里得距离)
• 曼哈顿距离
• 闵可夫斯基距离
• 切比雪夫距离
• 余弦距离

欧式距离

欧式距离代表的是两点之间的距离作为的衍生，比如现在在408教室上课，有位同学要去隔壁的508教室，不能根据距离直接穿过去，二维欧式距离公式如下：
$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$$
衍生三维欧氏距离公式如下：
$$d_{12}=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2+(z_1-z_2{)}^2}$$
归纳N维欧式距离公式如下：
$$d_{12}=\sqrt{\sum _{k=1}^n(x_i-y_i{)}^2}$$

• 涉及到开根号，就会涉及到浮点数，甚至是无线无限循环小数。在机器学习中的特征一般都是高纬(超越了3个维度)的，再涉及到小数，就会有误差，对内存的消耗很大，计算机的运行速度就会很慢。为了解决这个问题，就尽量的进行整数的计算，引入曼哈顿距离。

曼哈顿距离

在几何空间中用的比较多，比如a同学在408，b同学在512，从a到达b，中间的格子都是墙，不可能从a走绿色的线穿墙而过，最终目的也要使得路程最短。可以从a点先往上走，距离为$y_2$和$y_1$的差值，然后横向走，距离为$x_2$和$x_1$的差值，才能到达最终的终点。通过两段距离的和，求出两点之间的距离。
通过下图可以看出，不管如何顺着格子走，两点之间的距离是一定的。

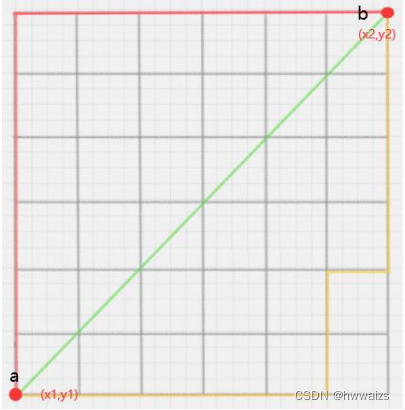
二维平面两点$a(x_1,y_1)$与$b(x_2,y_2)$间的曼哈顿距离：
$$d_{12}=|x_1-x_2|+\mid y_1-y_2\mid$$
n维空间点$a(x_{11},x_{12},...,x_{1n})$与$b(x_{21},x_{22},...,x_{2n})$的曼哈顿距离：
$$d_{12}=\sum _{k=1}^n(x_{1k}-x_{2k})$$

• 曼哈顿距离也被称为出租车几何，在城市中开车不能穿墙而过，只能根据房子周边的路线去走。在高维中进行整数计算，只用到了加减的运算，避免了小数的计算(不至于出现无线循环小数，或者是无理数)，运算速度比较快，并且误差很小。

切比雪夫距离

在国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子$(x_1,y_1)$走到格子$(x_2,y_2)$最少需要走多少步？这个距离就叫切比雪夫距离。

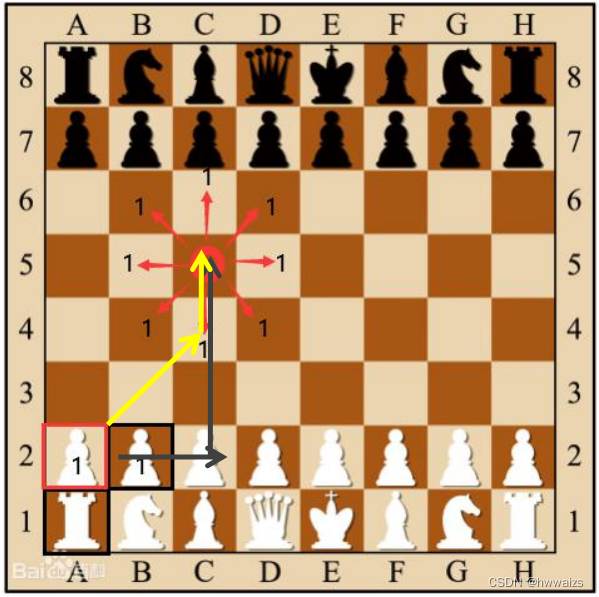
从上图可以看出从2A到5C点所经过的距离，可以是先从2A走到2C(2步)，然后从2C走到5C(3步)；也可以是先从2A走到4C(2步)，然后从4C走到5C(1步)。第二种走的步数刚好为第一中走的两部分步数的最大值。
二维平面两点$a(x_1,x_2)$与$b(x_2,y_2)$间的切比雪夫距离：
$$d_{12}=max(|x_1-x_2|,\mid y_1-y_2\mid )$$
n维空间点$a(x_{11},x_{12},...,x_{1n})$与$b(x_{21},x_{22},...,x_{2n})$的切比雪夫距离：
$$d_{12}=max(|x_{1i}-x_{2i}|)$$

闵可夫斯基距离

闵式距离是一类距离的同城，是对多个距离度量公式的概括性的表述。闵可夫斯基距离是个通过的指标，通过变换参数来更换极限形式，
两个n维变量$a(x_{11},x_{12},...,x_{1n})$与$b(x_{21},x_{22},...,x_{2n})$的闵可夫斯基距离定义为：
$$d_{12}=\sqrt[p]{\sum _{k=1}^n|x_{1k}-x_{2k}{|}^p}$$
其中p是一个变参数：

• 当$p=1$时，根号就不存在了，就是曼哈顿距离；
• 当$p=2$时，就是欧式距离；
• 当$p\to \infty$时，取极限的最大值，忽略最小值，就是切比雪夫距离

余弦距离

余弦距离实际上计算的是两个向量的夹角，是在方向上计算两者之间的差异，对绝对数值不敏感。sin函数是对边比斜边，cos函数是临边比斜边，引申出来两个向量之间的夹角余弦公式。夹角余弦的取值为-1到1，余弦越大就表示向量的夹角越小。
二维空间中向量$A(x_1,y_1)$与向量$B(x_2,y_2)$的夹角余弦公式：
$$cos\theta =\frac{x_1{x}_2+y_1{y}_2}{\sqrt{x_1^2+y_1^2}\sqrt{x_2^2+y_2^2}}$$
两个n维样本点$a(x_{11},x_{12},...,x_{1n})$与$b(x_{21},x_{22},...,x_{2n})$的夹角余弦为：
$$cos\theta =\frac{a\cdot b}{|a||b|}$$
即：$$cos(\theta )=\frac{{\sum }_{k=1}^n{x}_{1k}{x}_{2k}}{\sqrt{{\sum }_{k=1}^n{x}_{1k}^2}\sqrt{{\sum }_{k=1}^n{x}_{2k}^2}}$$

• 余弦距离也被称为余弦相似度，可以判断两个物品间的相关性，
  比如3个人去超市买物品，用表格表示，买的为1，没有买的为0。

物品人员	a	b	c	d	e
A	1	1	0	0	1
B	0	1	1	0	0
C	1	0	0	0	1

A与B的相似度：$cos(\theta )=\frac{1\ast 0+1\ast 1+0\ast 1+0\ast 0+1\ast 0}{\sqrt{1^2+1^2+0^2+0^2+1^2}\sqrt{0^2+1^2+1^2+0^2+0^2}}=\frac{1}{\sqrt{6}}=0.408$

A与C的相似度：$cos(\theta )=\frac{1\ast 1+1\ast 0+0\ast 0+0\ast 0+1\ast 1}{\sqrt{1^2+1^2+0^2+0^2+1^2}\sqrt{1^2+0^2+0^2+0^2+1^2}}=\frac{2}{\sqrt{6}}=0.816$

B与C的相似度：$cos(\theta )=\frac{0\ast 1+1\ast 0+1\ast 0+0\ast 0+0\ast 1}{\sqrt{0^2+1^2+1^2+0^2+0^2}\sqrt{1^2+0^2+0^2+0^2+1^2}}=\frac{0}{\sqrt{4}}=0$

由此可见，A与C的相似度较高，可以根据A用户购买的物品给与A相似度较高的C进行推荐。

KD树

有位置的数据想要去预测类别，找到跟他最临近的k个邻居，把这个点跟所有邻居的距离都算一下，进行排序，找到最近的k个来取众数，以此来划分到最多的类别中。对于数据比较少的情况，计算速度比较快，如果要训练好一个数据模型，数据量必然是很大的，再去一个一个的计算预测数据与每个邻居之间的距离，计算量就会特别的大，可以使用KD树进行优化。

KNN 的计算过程是大量计算样本点之间的距离。为了减少计算距离次数，提升 KNN 的搜索效率，提出了 KD 树（K-Dimensional 的缩写）。KD 树是对数据点在 K 维空间中划分的一种数据结构。在 KD 树的构造中，每个节点都是 k 维数值点的二叉树。既然是二叉树，就可以采用二叉树的增删改查操作，这样就大大提升了搜索效率。

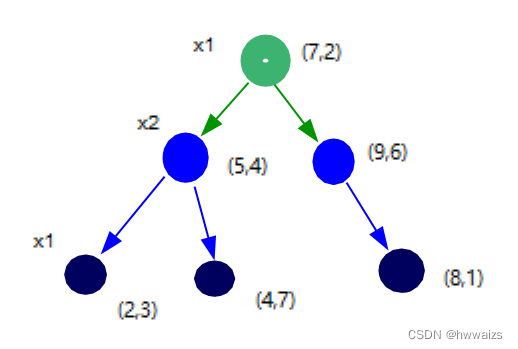
• 例题1：有数据集{(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}，构造kd树。
  
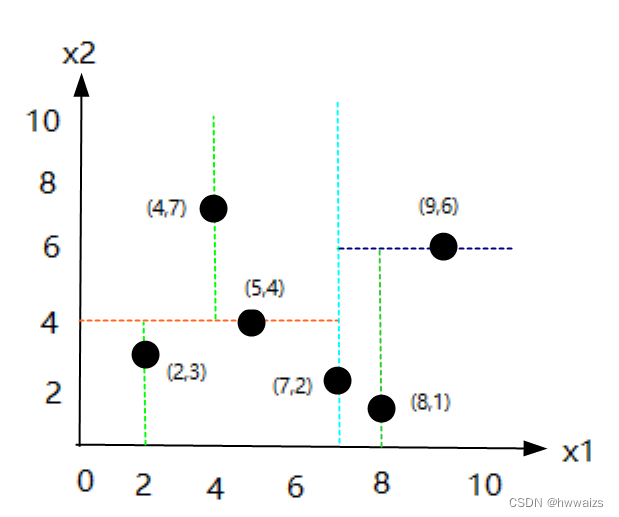
  六个数据点为二维的点，呈现在二维的坐标轴上，kd树的划分：

• 1.以x1轴的中位数作为切分标准，2，4，5，7，8，9，把几个数从小到大排序，个数为偶数的话，选取中间的两个点，相加求中位数，(5+7)/2=6，
  • 1.(5,4)与(7,2)距离6同样近，取任意的一个点如取(7,2)作为根节点
  • 2.做一条过(7,2)点垂直于x1轴的线，把二维的屏幕划分为左右两部分
• 2.以x2轴来划分左边区域，找到中位数，做x2的垂直线，
  • 1.左边区域有3个点，x2的值分别为3，4，7，中位数点为(5,4)，
  • 2.过(5,4)做一条垂直于x2的线，把左边的区域分为上下两部分，
  • 3.以x1轴划分下区域，除了已成为节点的点，下区域就剩下了(2,3)点，通过(2,3)向x1做垂线，
  • 4.以x1轴划分上区域，除了已成为节点的点，上区域就剩下了(4,7)点，通过(4,7)向x1做垂线，
  • 5.在二叉树上放置的点是左小右大，所以把(2,3)点放在左侧，(4,7)点放在右侧
• 3.以x2轴来划分右边区域，找到中位数，做x2的垂直线
  • 1.只剩下(8,1)与(9,6)，所以中位数距离两个点的距离一致，随意取一个点作为节点，如取(9,6)
  • 2.过 (9,6)向x2轴做垂线，把右边区域也分为上下两部分，上部分已经没有点了
  • 3.下半部分找到(8,1)的中位数，只有一个点，这个点就是中位数，通过这个点向x1轴做垂线，得到的最后一个节点为(8,1)
    
• 例题2，有目标点(3,4.5)，请问如何在数据集中搜索目标点的最近邻？
  
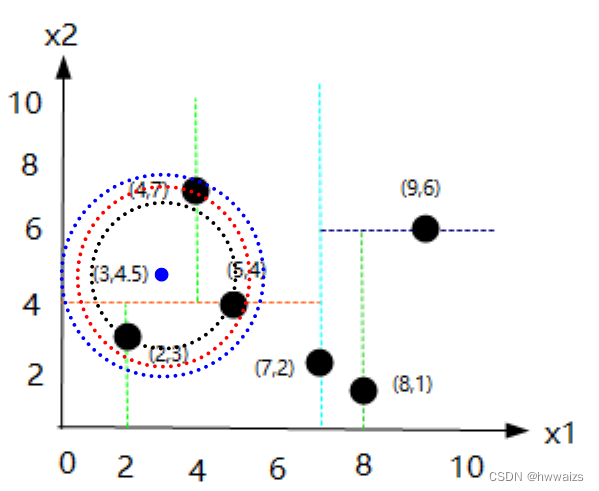
  如果取计算每个点的距离，就要去计算6次，如果数据量很大的话，计算量就会越来越多。用kd树进行计算，本身就是个递归，重复的过程。

• 1.从根节点(7,2)来判断，点(3,4.5)x1轴上的数为3，3小于7，左边为较小的数，就找到了点(5,4)，x2维度上的数为4，4.5大于4，会往右侧方向找(较大的数)，找到了点(4,7)，此时暂时的最近邻为(4,7)，
• 2.以(3,4.5)为圆心，到点(4,7)的距离为半径画圆，得到了蓝色的圆，很显然(4,7)不是点(3,4.5)的最近邻，此时算法要进行回溯，以目标点为圆心，以到暂时的临近点为半径，做圆，两点间的半径为2.69
• 3.回溯到上个节点(5,4)，以目标点为圆心，以到暂时的临近点(5,4)为半径，做圆，两点间的半径为2.06
• 4.继续进行回溯到(2,3)，以目标点为圆心，以到暂时的临近点(2,3)为半径，做圆，两点间的半径为1.8，
  得到(2,3)才是最近邻的点，此时就不需要去计算距离(7,2)，(9,6)，(8,1)的距离了，减少了计算量。

数据集获取

要测试一些算法，如果不是在真实的环境中，缺少特征工程的数据，学这些模型的时候就可以借鉴已经做好处理的数据来进行学习。

获取函数

获取数据的接口

sklearn.datasets 加载获取流行数据集
datasets.load_***() 获取小规模数据集，数据包含在datasets里
datasets.fetch_***(data_home=None) 获取大规模数据集，需要从网络上下载，
函数的第一个参数是data_home，表示数据集下载的目录,默认是 ~/scikit_learn_data/

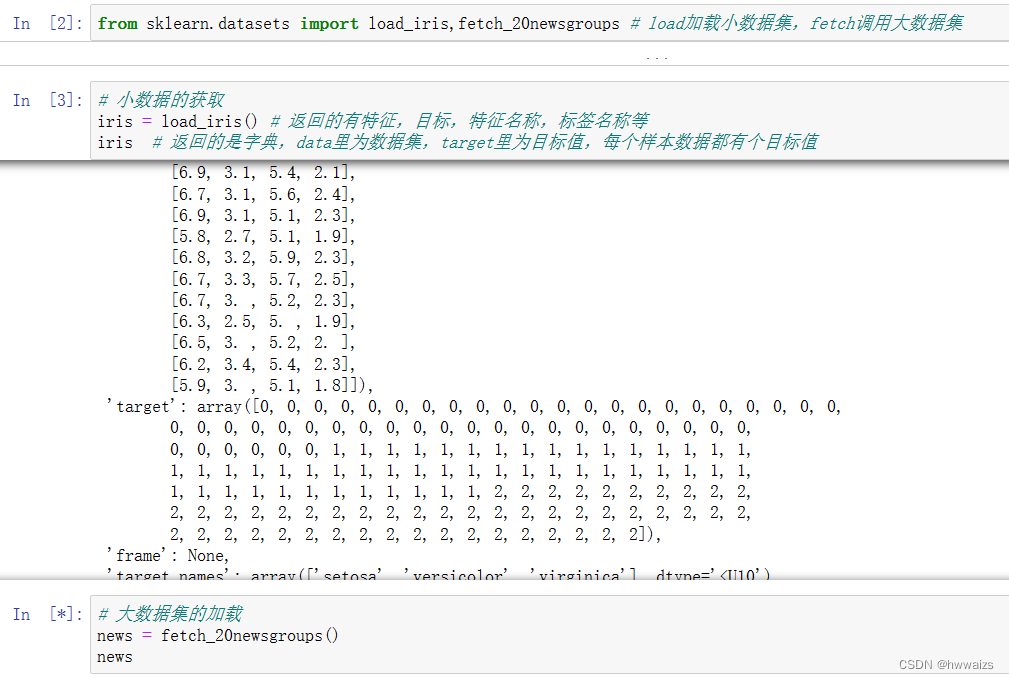
返回集

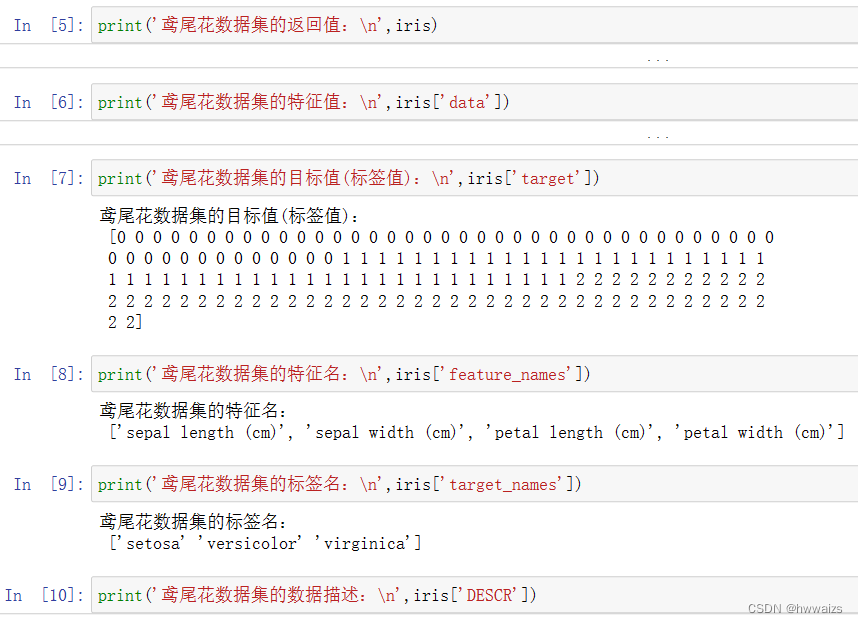
load 和 fetch 返回的数据类型(字典格式)
data：特征数据数组
target：标签数组
DESCR：数据描述
feature_names：特征名
target_names：标签名

数据分割

训练模型需要一部分数据，评估模型的好坏需要一部分新的数据，两份数据重合的时候会产生状况，导致结果不真实，所以把数据分为训练集、测试集以及验证集，在没有调参之前把数据分为训练集和测试集。数据分割的方式：留出法，直接以二八或者三七分数据；K折交叉验证，把数据集分为10份，依次以1份作为测试集，其他的作为训练集，得出10次的结果求平均；自助法，训练集随机进行有放回的抽取。最常用的是留出法。

留出法api

用程序实现，把数据集分为3份和7份，用numpy、pandas的选择数据来做，求出数据的总长度，然后做切割，用sklearn来做训练集的测试分割。

sklearn.model_selection.train_test_split(arrays,*options)
x 数据集的特征值
y 数据集的标签值
test_size 测试集的大小，一般为float
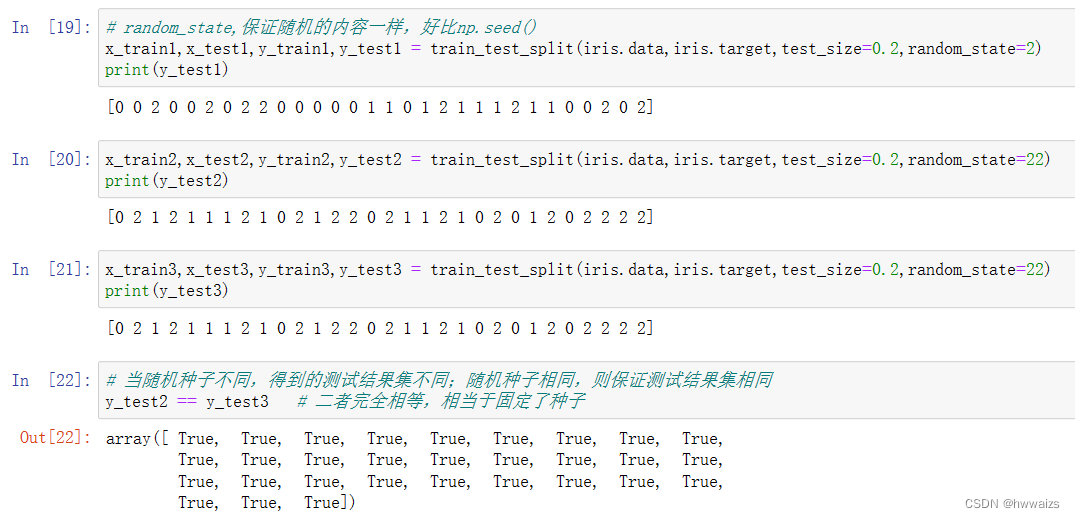
random_state 随机数种子,不同的种子会造成不同的随机采样结果。相同的种子采样结果相同。
return 训练特征值，测试特征值，训练目标值，测试目标值

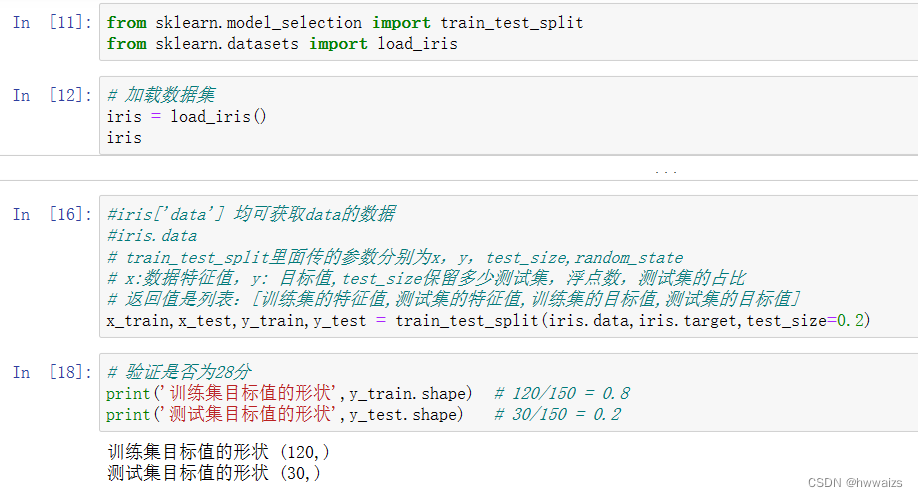
算法、模型都存在随机性，同一个算法、同一个数据集运行多次的时候结果是不一样的，同一个代码、同一个模型不同人训练出来的结果会有差异。数据分割同样也具有随机性，可以使用random_state参数，保证每次训练出来的结果是一样的。