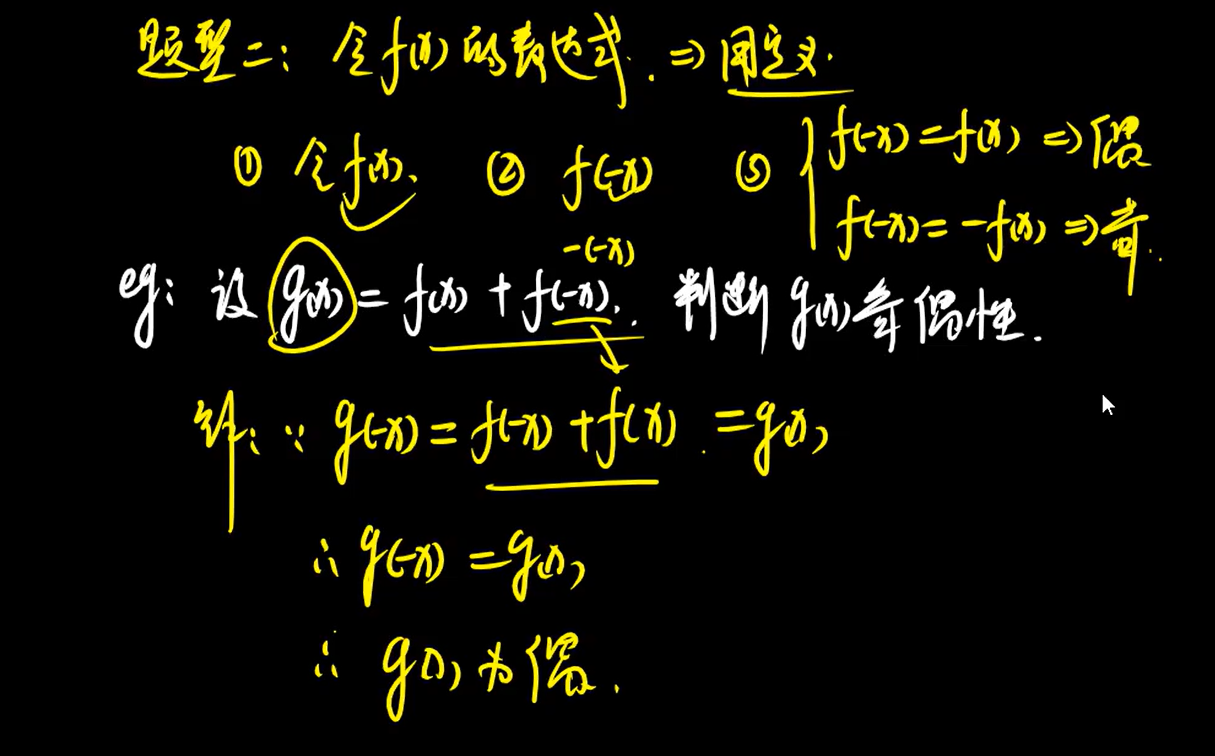---

---

考点

1、定义域

对于一个 y= f(x) 的函数而言，定义域是求 x 的取值范围

2、对应法则

对于一个函数 y = f(x) 而言，f 表示该函数的对应法则，即对自变量 x 的加工处理方式，就象代码中不同的函数，当我们的参数 x 想要得出不同的 因变量 y 就需要调用不同的函数进行对自变量 x 的计算，返回一个 y ，可以把 f 对应法则 看作一个 函数方法名 常用 f (x ) g(x) h(x) 表示，只是换了个名字而已。

---

一、函数的概念

1、自变量 x , 因变量 y，一一对应，因此有公式 y = f (x)

自变量 x 就和我们写程序的函数形参一样，将形参扔进去一个函数里面，就会得到函数的返回值，也就是因变量 y。

2、定义域

具体函数的定义域 （送分题）

真题

1、

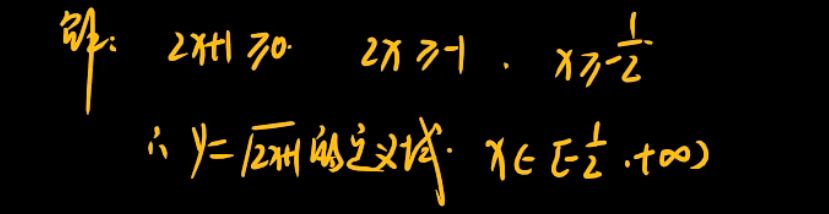
2、

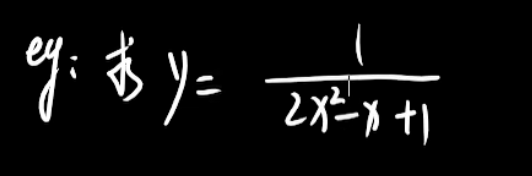
解题思路：
这里一看 分母就可以进行十字交叉相乘，条件是不等于 0

3、

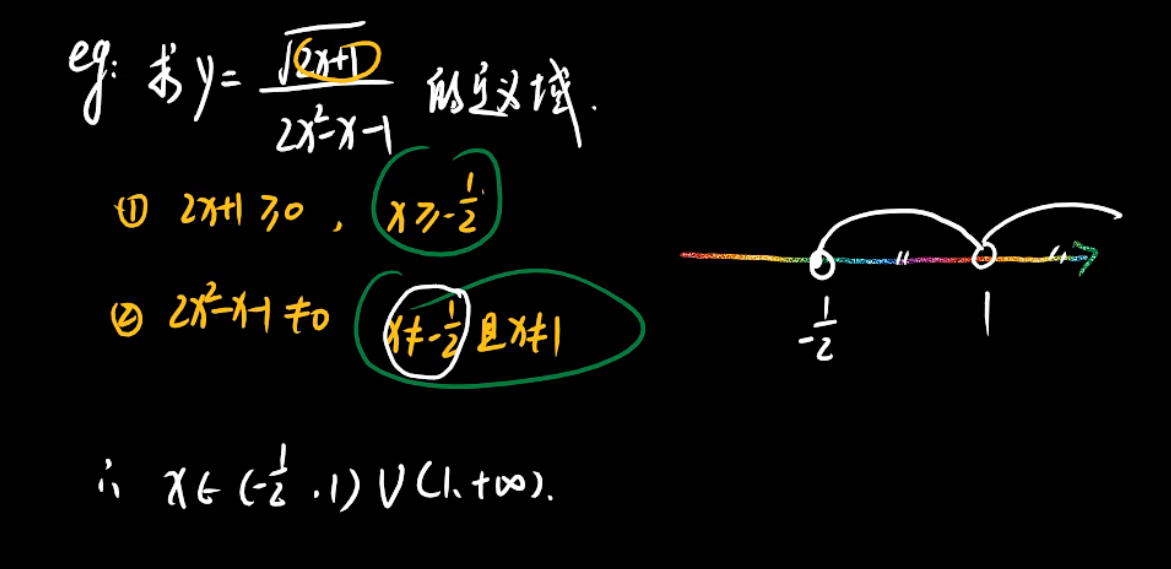
4、

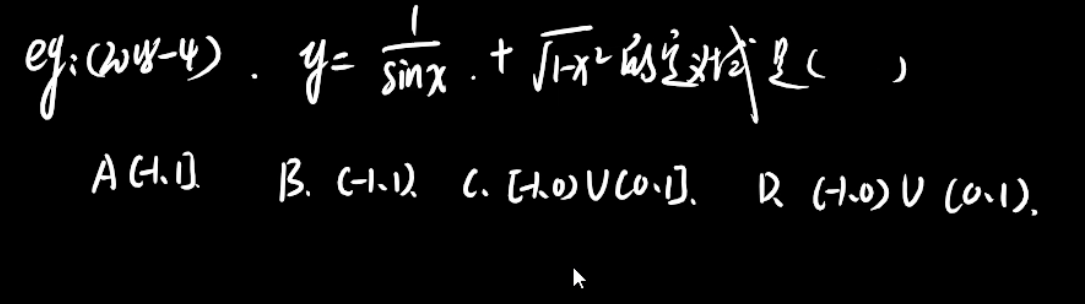
抽象函数的定义域

真题

1、

2、

3、根据函数的对应法则求函数表达式

题型 一

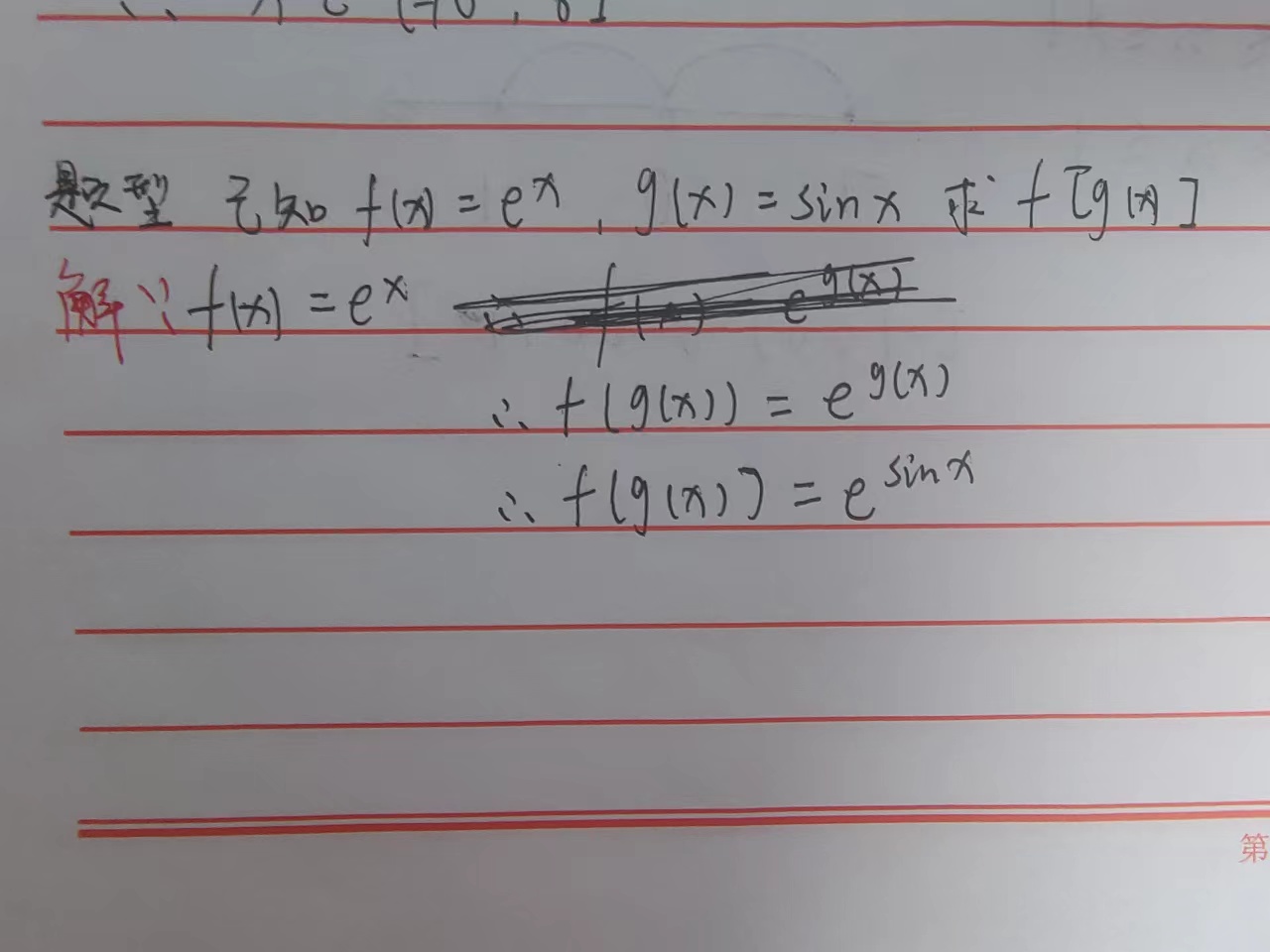
题型 二

第一种解题法，换元法，化繁为简

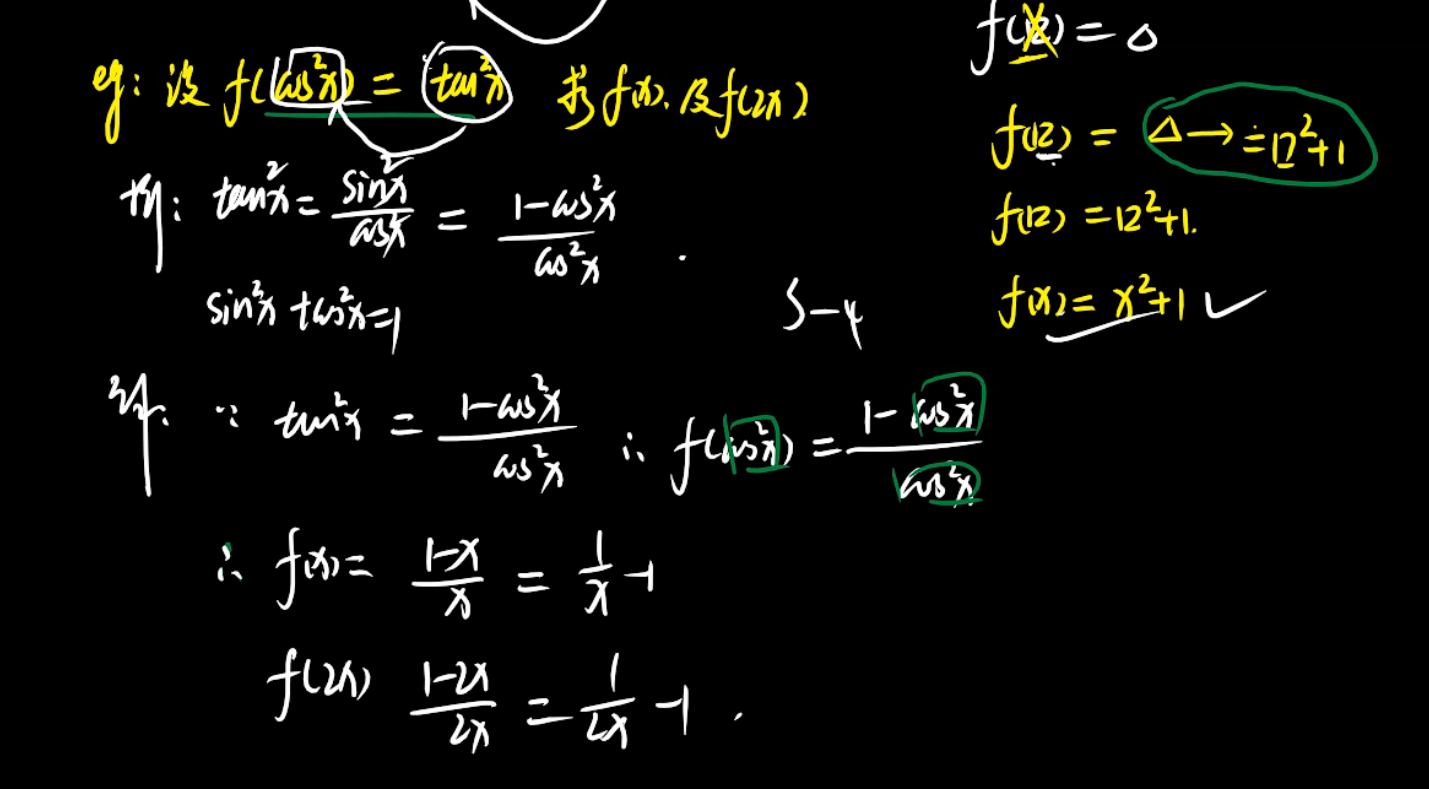
解法二 配凑法，后面往前面凑分母

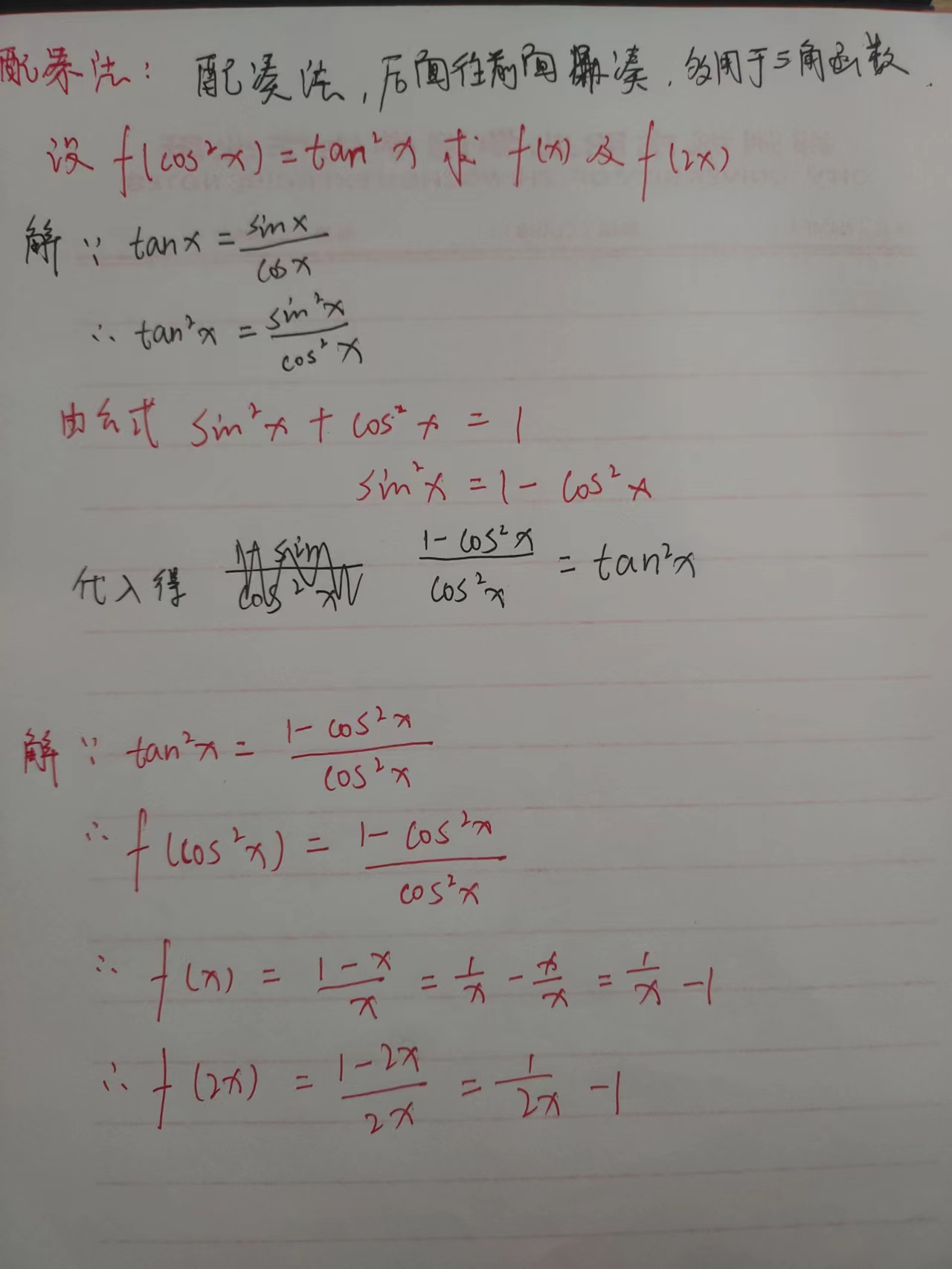
4、反函数

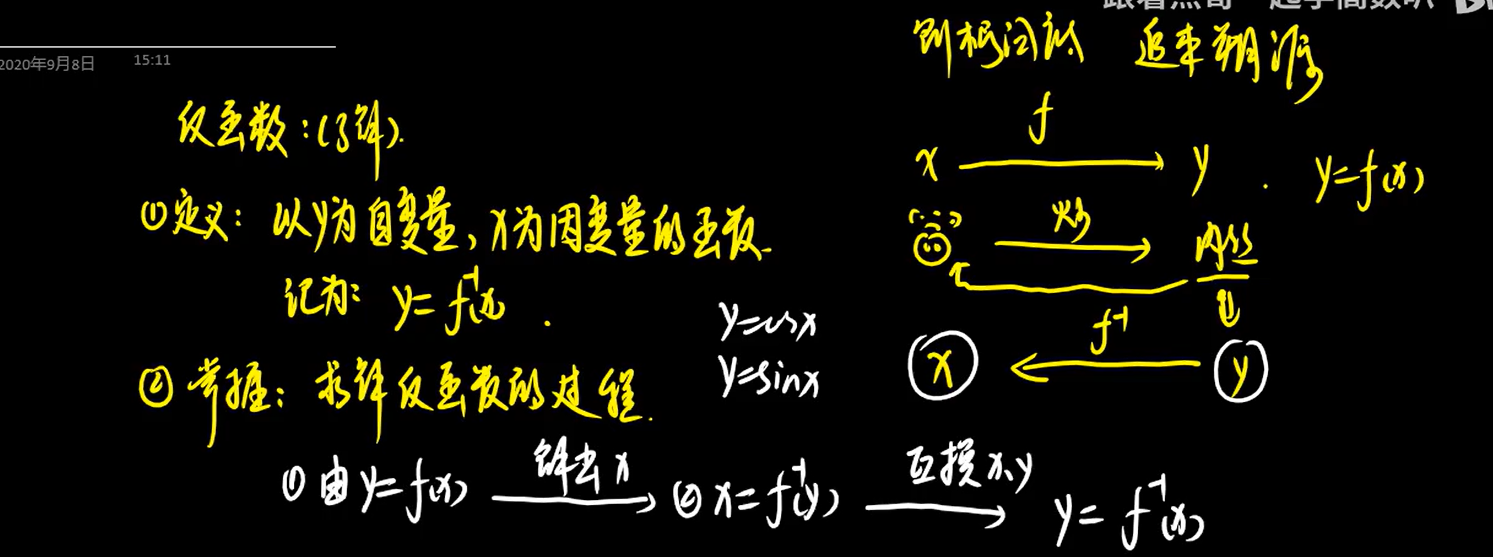
二、常见的基本初等函数

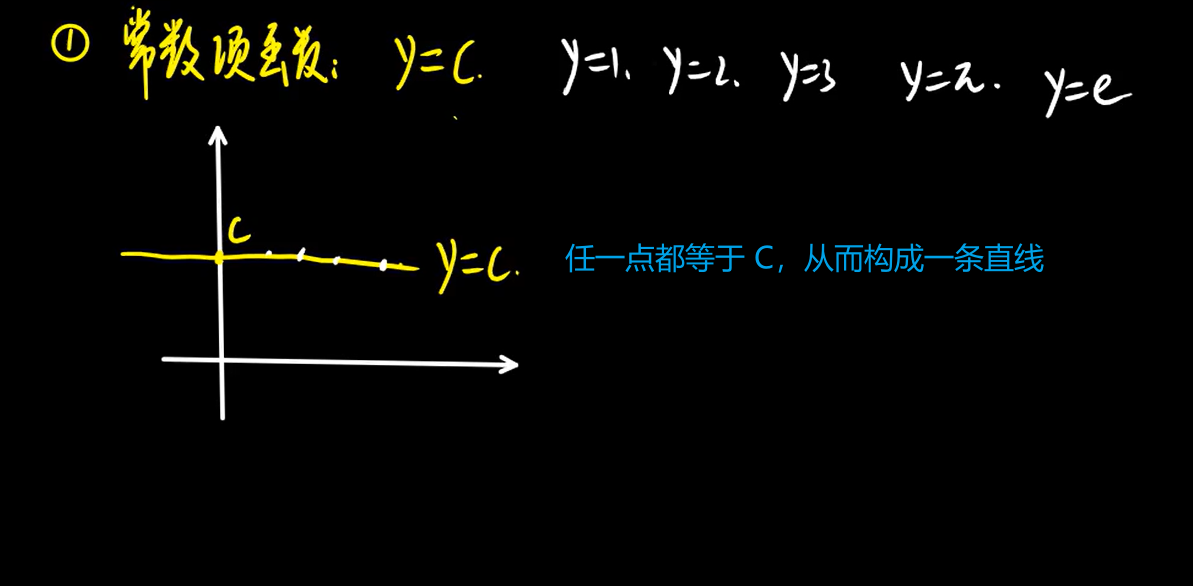
1、常数项函数

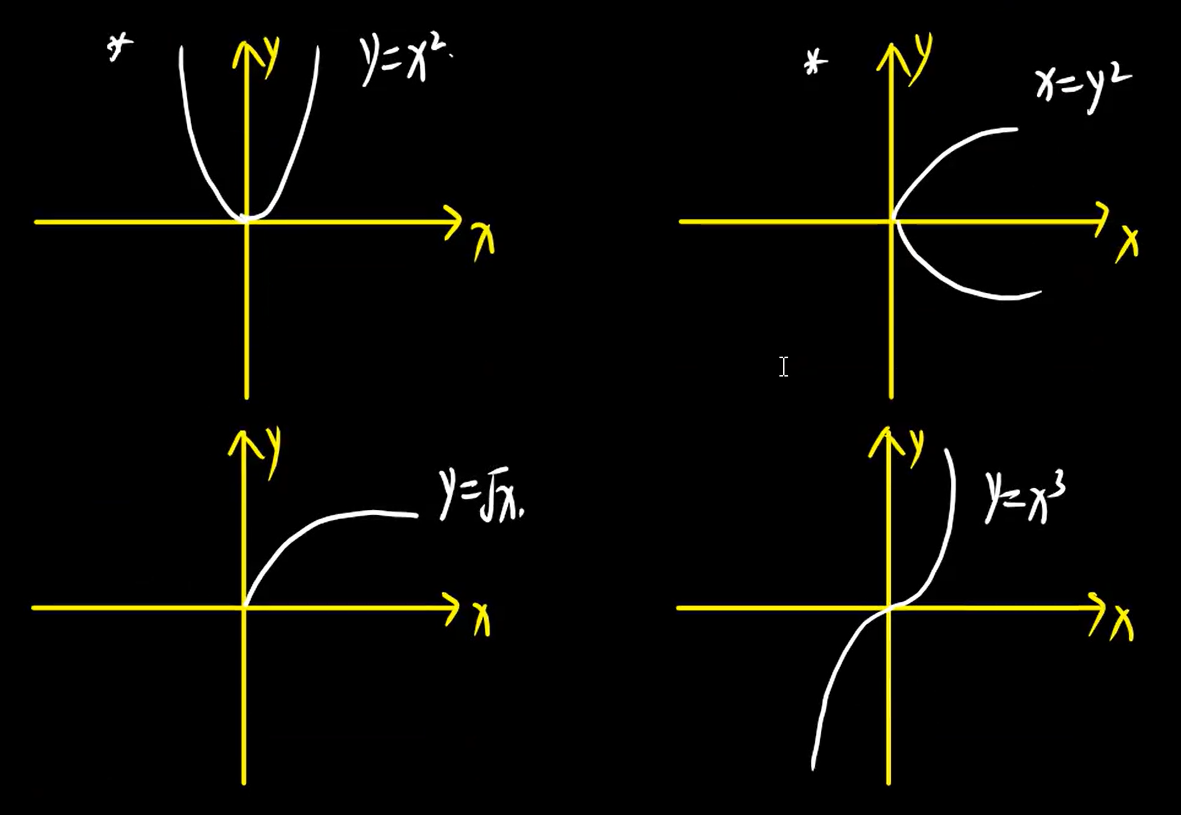
2、幂函数

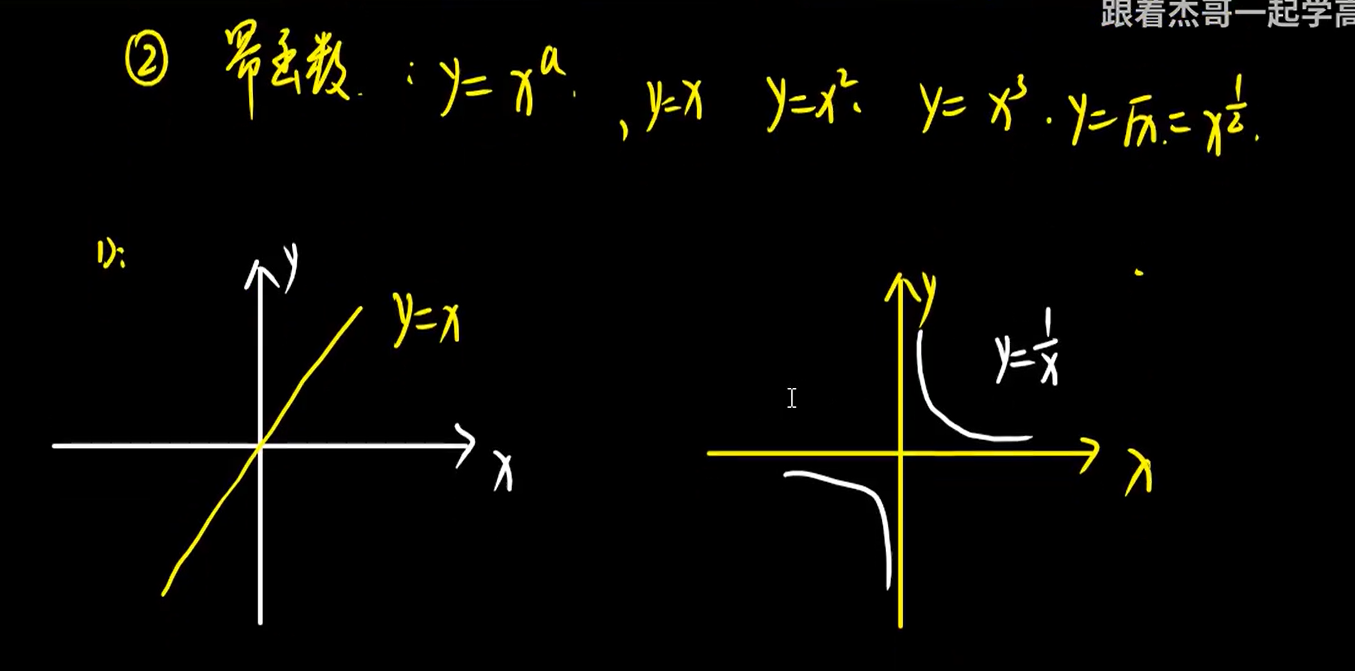
常用公式

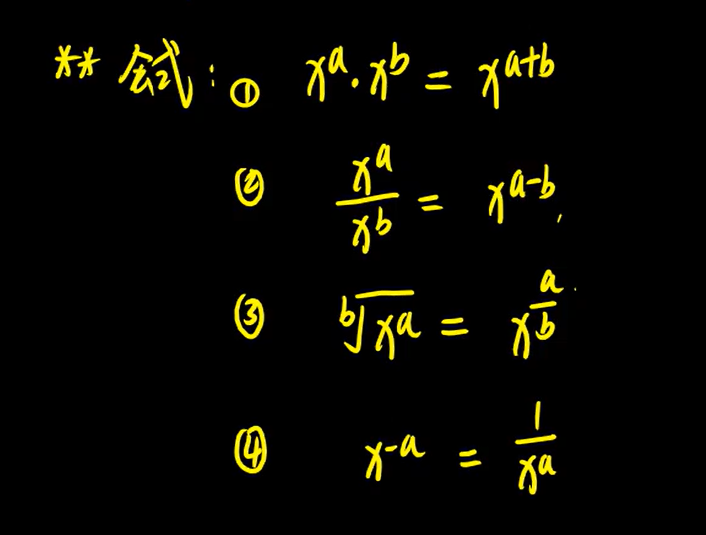
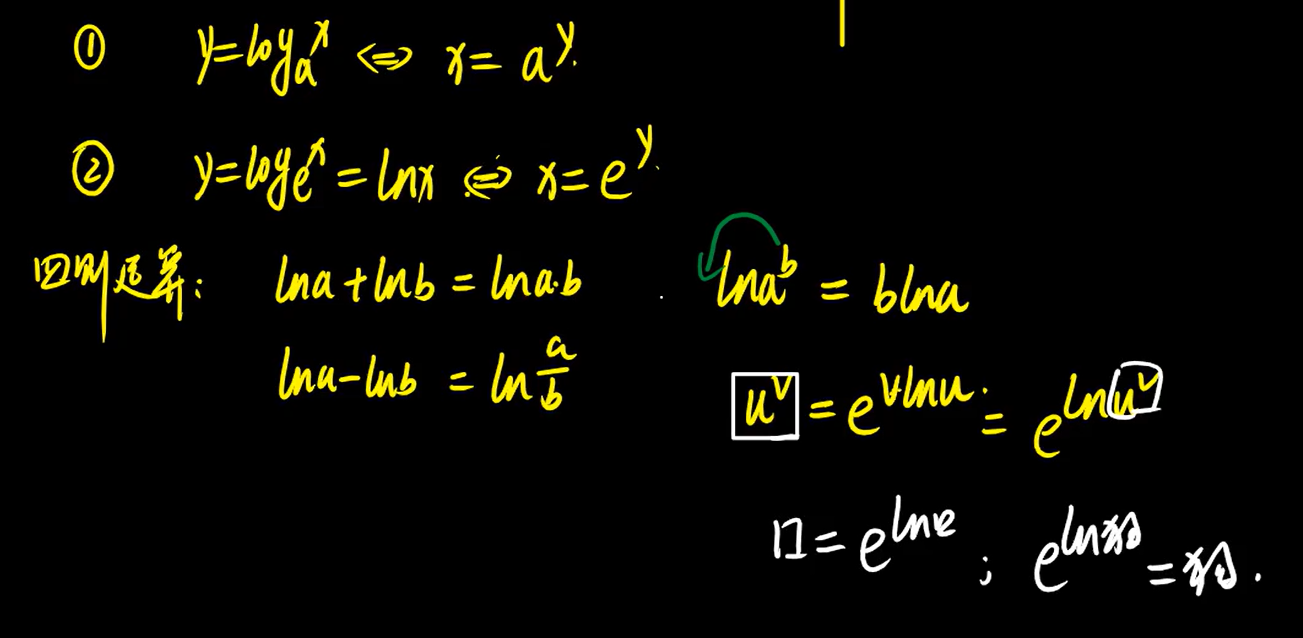
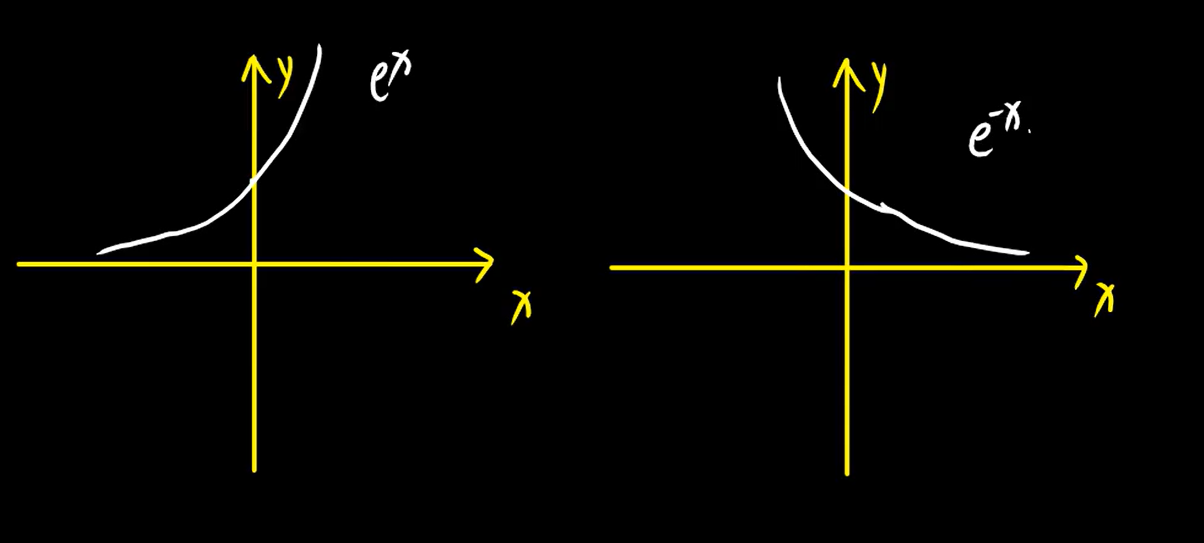
3、指数函数

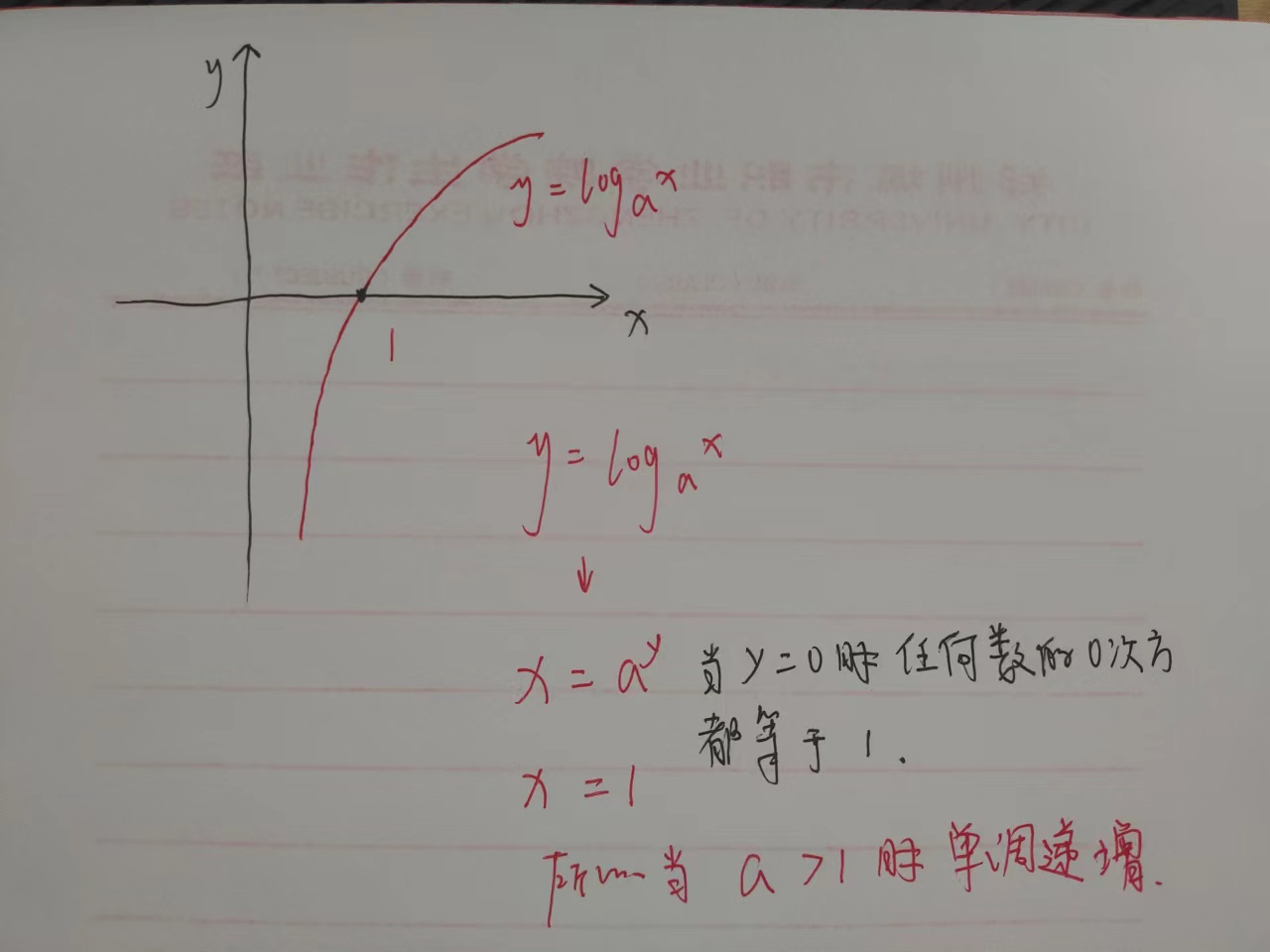
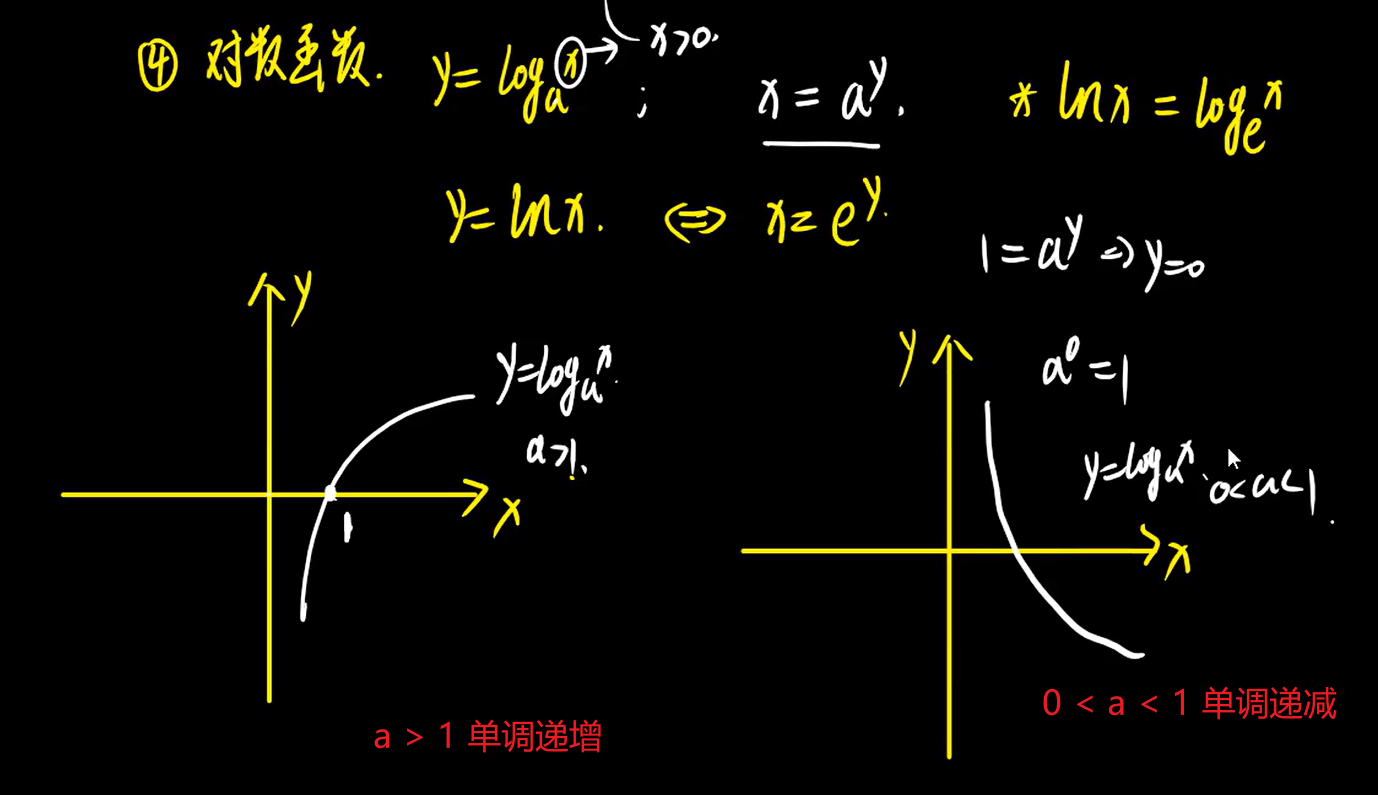
4、对数函数

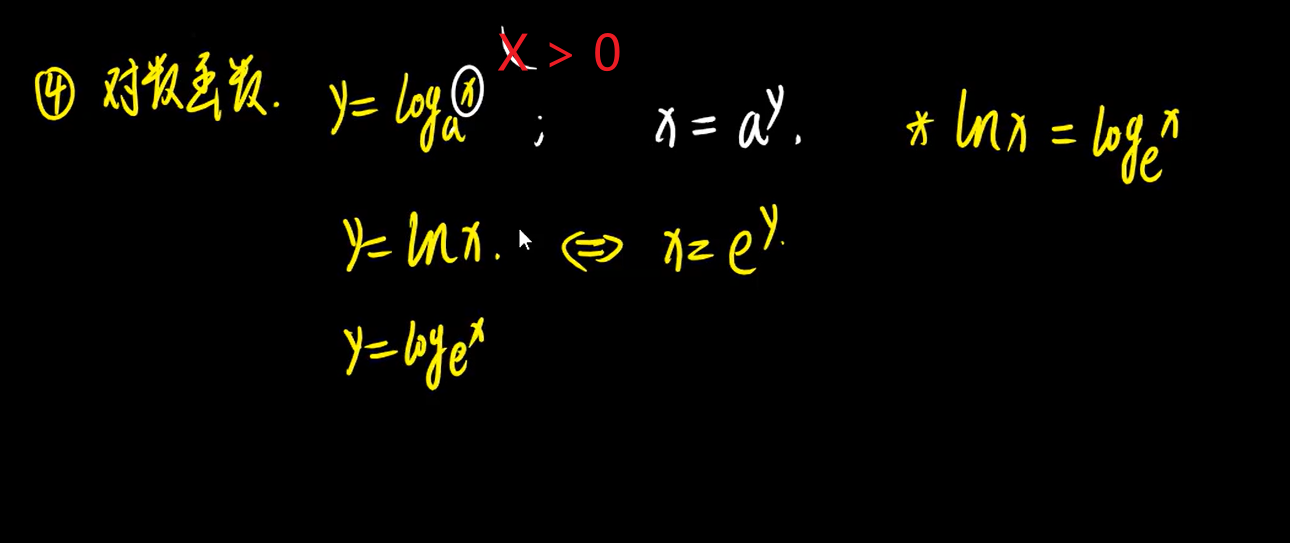
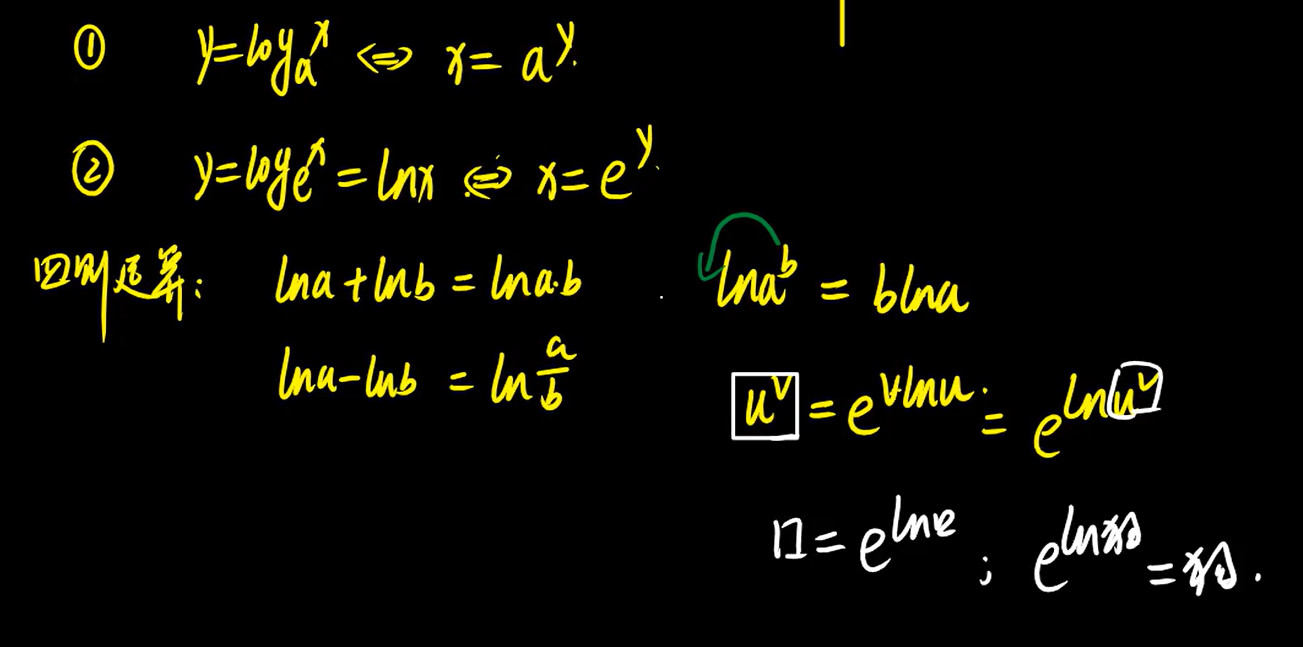
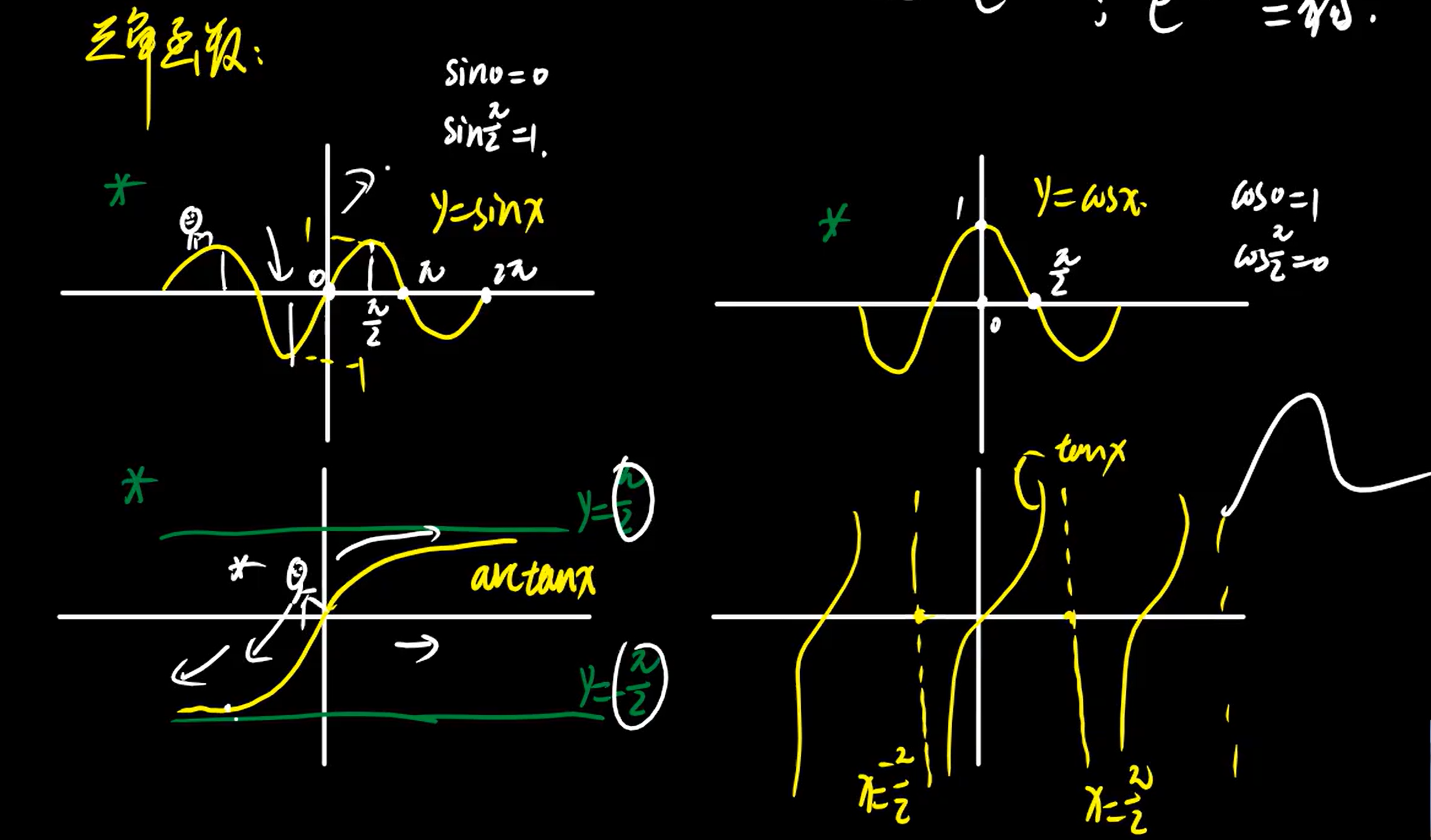
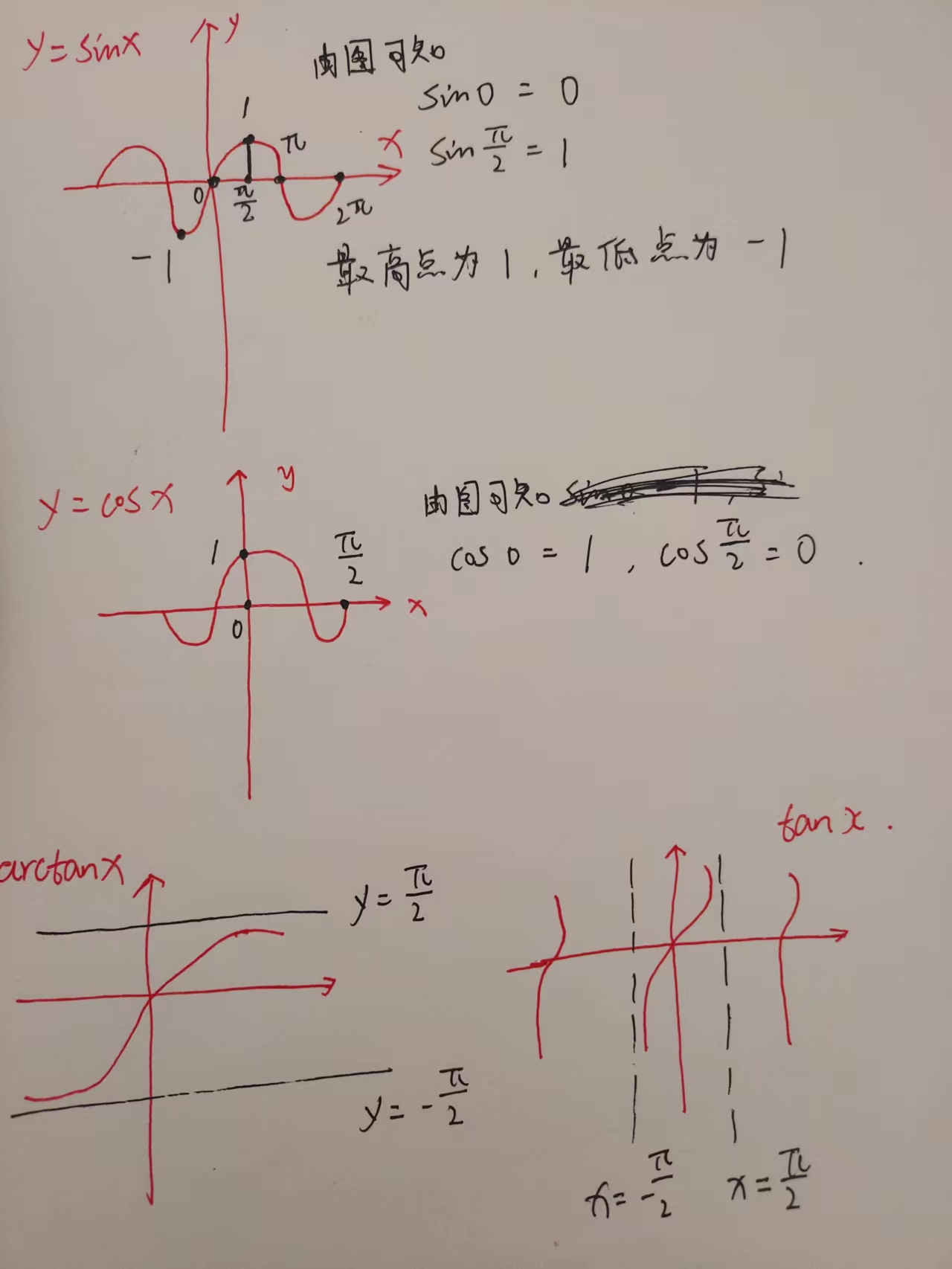
5、三角函数

6、三角函数的值，以及运算公式

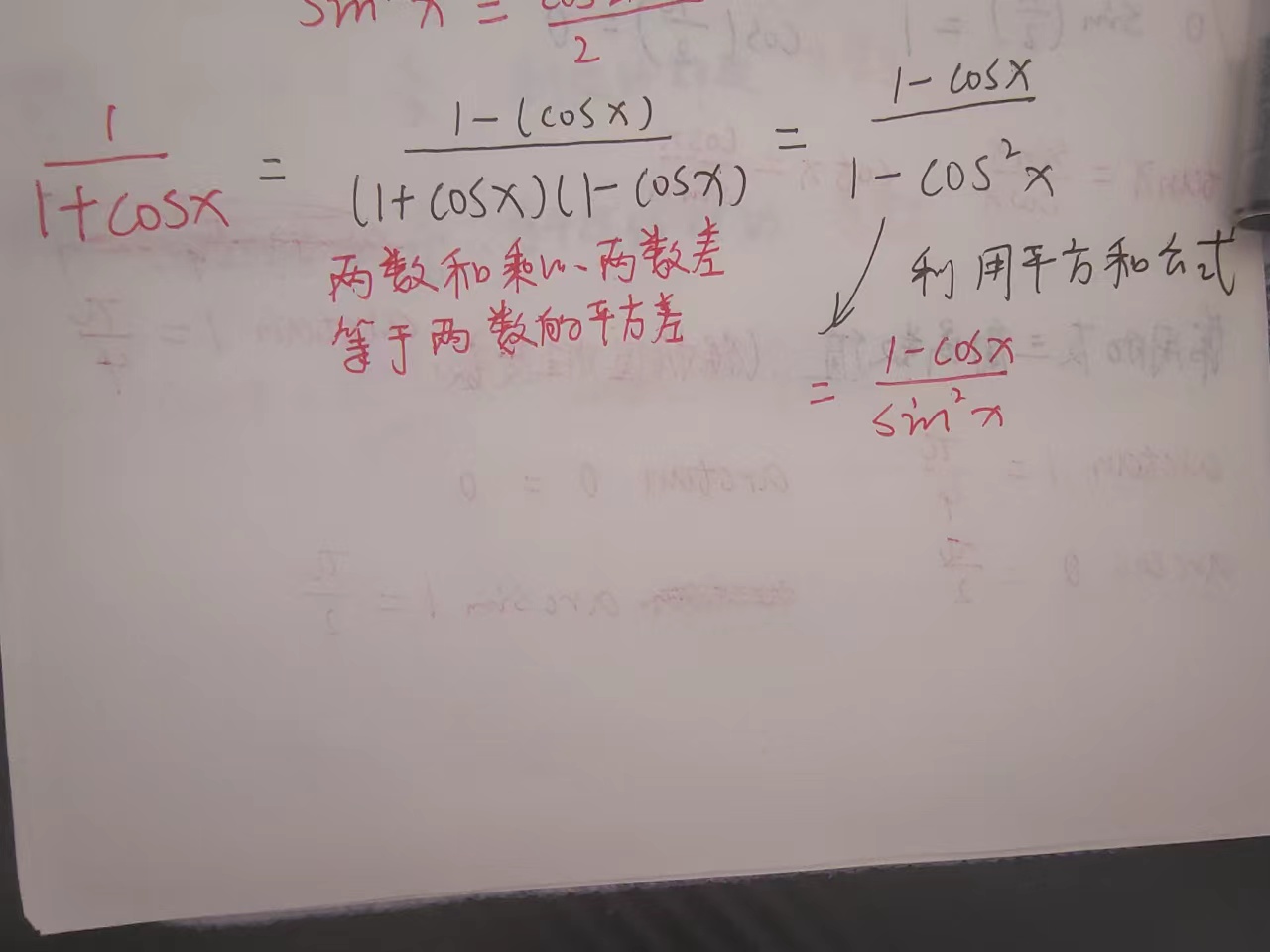
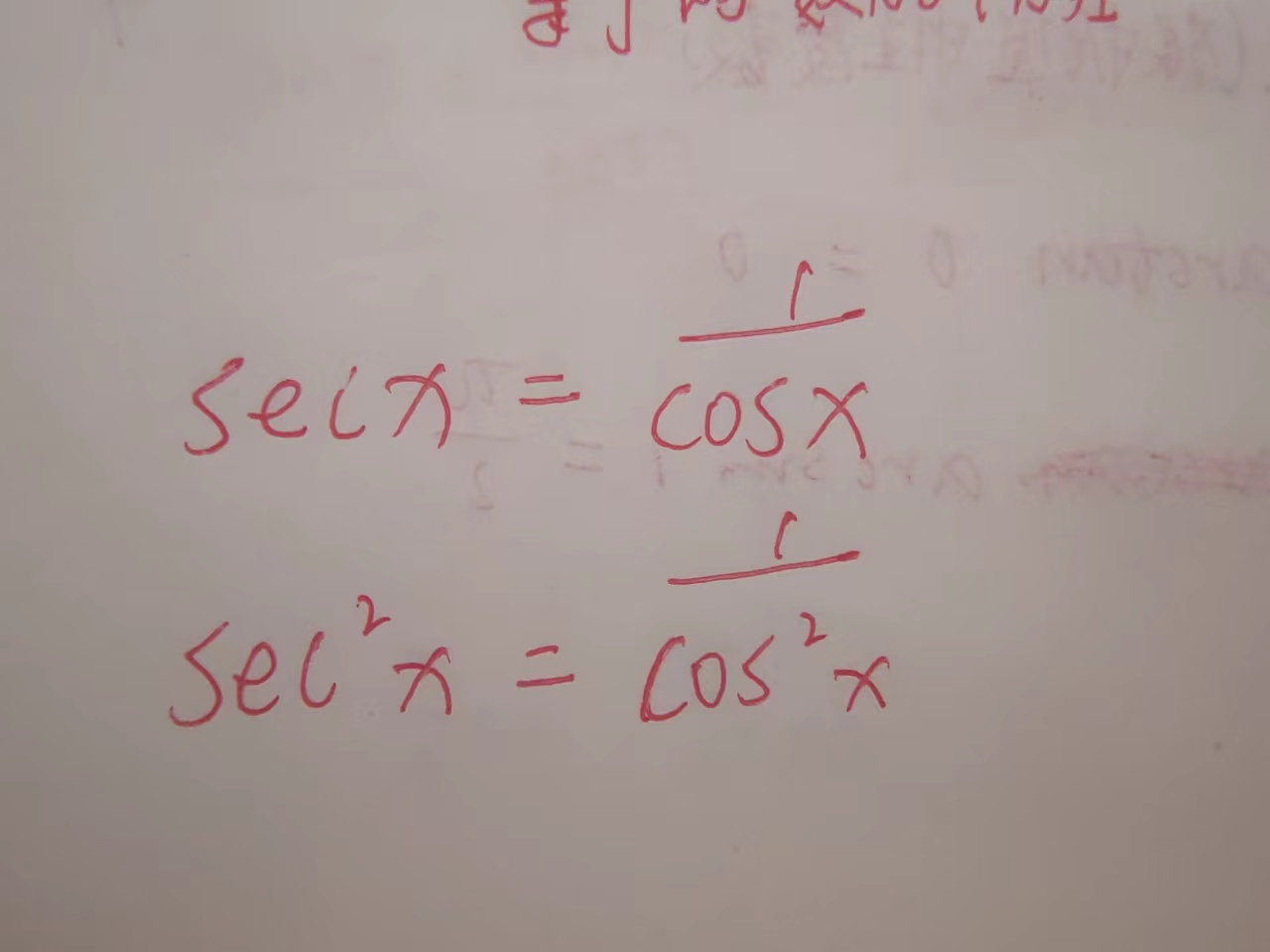
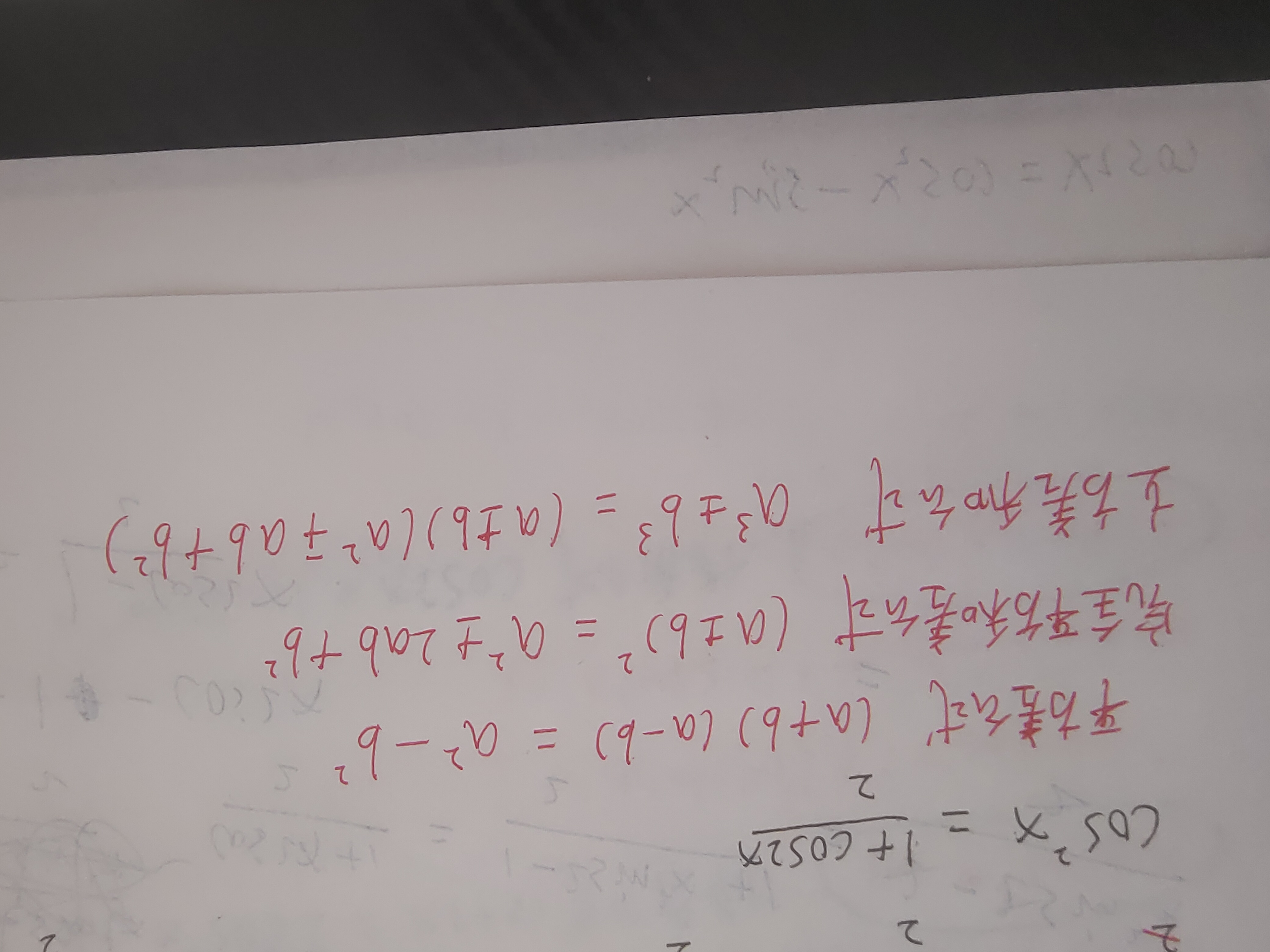
三、 复合函数及其分解，函数套娃

分解原则： 从外向里，层层递进，直到分解到含 x 的基本初等函数为止

四、函数的奇偶性

1、常见的奇偶函数

2、奇偶函数的四则运算性质

3、复合函数的奇偶性