题目
给定一个n(2<=n<=2e5)位的数字串X,
可以将X划分成若干段,得分为每一段的乘积(可以不分割,此时得分为X)
求所有种分法的得分之和,答案对998244353取模
思路来源
洛谷题解
[ABC288F] Integer Division 题解 - spider_oyster 的博客 - 洛谷博客
题解
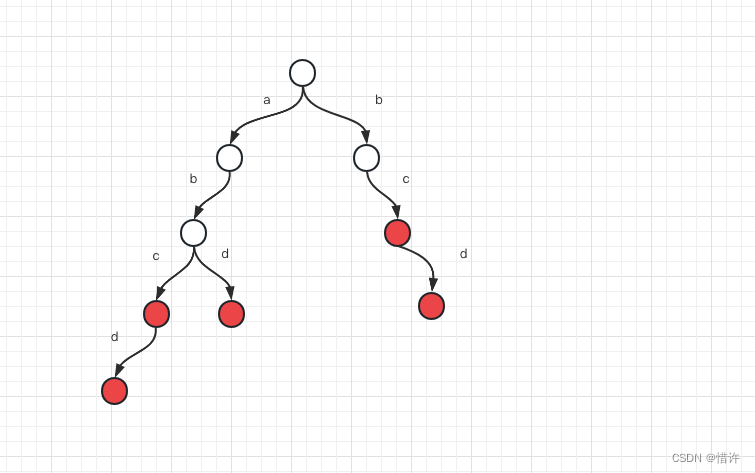
图片摘自[ABC288F] Integer Division 题解 - spider_oyster 的博客 - 洛谷博客

先考虑暴力的做法,
dp[i]表示到考虑到第i位时的分法之和,
枚举最后一段取什么,复杂度是O(n^2)的
将最后一段的数字的贡献,拆成前后两部分,
发现前一部分可以用dp[i-1]表示,于是前缀和优化即可
计:,
则
其中,v[i]是第i位的数字的值
代码
其实dp数组改为维护两个变量即可,
因为只需要用到dp[i]和dp[i-1]
#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define pb push_back
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
std::mt19937_64 gen(std::chrono::system_clock::now().time_since_epoch().count());
ll get(ll l, ll r) { std::uniform_int_distribution<ll> dist(l, r); return dist(gen); }
const int N=2e5+10,mod=998244353;
int n,dp[N],sum;
char s[N];
int main(){
sci(n);
scanf("%s",s+1);
rep(i,1,n){
int v=s[i]-'0';
dp[i]=(10ll*dp[i-1]+1ll*(sum+1)*v)%mod;
sum=(sum+dp[i])%mod;
}
pte(dp[n]);
return 0;
}