前言

字典树又称为前缀树或Trie树，是处理字符串常见的数据结构。

字典树是一种树形结构，优点是利用字符串的公共前缀来节约存储空间，比如插入"abc"、“abcd”、
“abd”、“bc”、"bcd"之后，字典树结构如下【图中结点表红，表示有单词以此结点结尾】：

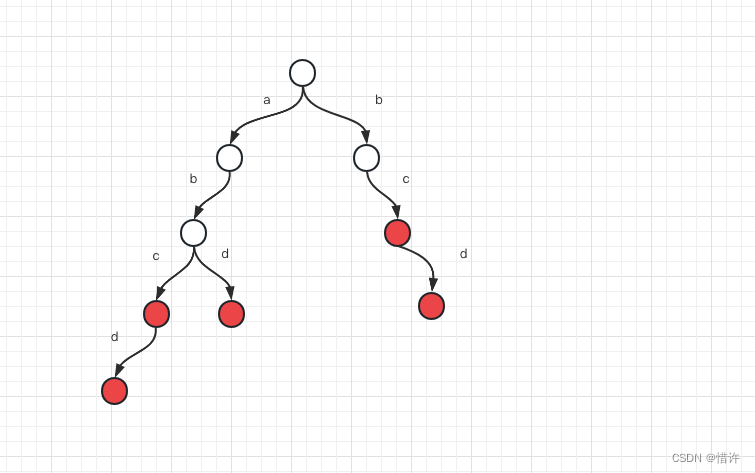
字典树基本性质如下：

• 根节点没有字符路径。除根节点外，每一个节点都被一个字符路径找到。
• 从根节点出发到任何一个节点，如果将沿途经过的字符连接起来，一定为某个加入过
  的字符串的前缀。
• 每个节点向下所有的字符路径上的字符都不同。

题目

字典树又称为前缀树或 Trie 树，是处理字符串常见的数据结构。假设组成所有单词的字符
仅是“a”~“z”，请实现字典树结构，并包含以下四个主要功能。

• void insert(String word)：添加 word，可重复添加。
• void delete(String word)：删除 word，如果 word 添加过多次，仅删除一个。
• boolean search(String word)：查询 word 是否在字典树中。
• int prefixNumber(String pre)：返回以字符串 pre 为前缀的单词数量。

思路

以在字典树中搜索是否添加过单词为例：

1. 从根结点开始搜索。

2. 取得要查找单词的第一个字母，并根据该字母选择对应的字符路径向下继续搜索。

3. 字符路径指向的第二层结点上，根据第二个字母选择对应的字符路径向下继续搜索。

4. 一直向下搜索，如果单词搜索完后，找到的最后一个结点是一个终止结点，比如上图中的实心结点，说明字典树中含有这个单词，如果找到的最后一个结点不是一个终止结点，说明单词不是字典树中添加过的单词。如果单词没搜索完，但是已经没有后续的结点了，也说明单词不是字典树中添加过的单词。

插入流程与此类似；

代码实现

    private static class TireNode {
        /**
         * 表示有多少单词共用这个结点
         */
        public int path;

        /**
         * 表示有多少个单词以这个结点结尾
         */
        public int end;

        /*
         * 每个结点路径上支持存储a-z共26个字母
         */
        public TireNode[] nexts;

        public TireNode() {
            path = 0;
            end = 0;
            nexts = new TireNode[26];
        }

    }


    public static class Trie {
        private TireNode root;

        public Trie() {
            root = new TireNode();
        }

        /**
         * 插入单词
         *
         * @param word
         */
        public void insert(String word) {
            if (word == null) {
                return;
            }
            char[] array = word.toCharArray();
            //先移动到头结点处
            TireNode node = root;
            int index = 0;
            for (int i = 0; i < array.length; i++) {
                //计算得到字母ASCII对应的偏移量index 0 - 25
                index = array[i] - 'a';
                if (node.nexts[index] == null) {
                    //如果没有生成路径，则创建路径下一结点
                    node.nexts[index] = new TireNode();
                }
                //移动到下一结点，共用路径+1
                node = node.nexts[index];
                node.path++;
            }
            //最终结点对应end+1
            node.end++;

        }

        /**
         * 查找单词
         *
         * @param word
         * @return
         */
        public int search(String word) {
            if (word == null) {
                return 0;
            }
            char[] chars = word.toCharArray();
            TireNode node = root;
            int index = 0;
            for (int i = 0; i < chars.length; i++) {
                index = chars[i] - 'a';
                if (node.nexts[index] == null) {
                    //表示当前路径上没有存储此字母，直接返回0
                    return 0;
                }
                node = node.nexts[index];
            }
            //如果最终结点end>0，表示单词存在
            return node.end;
        }


        /**
         * 删除单词
         *
         * @param word
         */
        public void delete(String word) {
            if (search(word) == 0) {
                return;
            }
            char[] chars = word.toCharArray();
            TireNode node = root;
            int index = 0;
            for (int i = 0; i < chars.length; i++) {
                index = chars[i] - 'a';
                //此单词路径path需要--，如果为0表示不需要后续结点，直接置null
                if (--node.nexts[index].path == 0) {
                    node.nexts[index] = null;
                    return;
                }
                node = node.nexts[index];
            }
            //最后结点对应end数量-1
            node.end--;
        }

        /**
         * 查找字典树中存在多少单词以pre为前缀
         *
         * @param pre
         * @return
         */
        public int prefixNumber(String pre) {
            if (pre == null) {
                return 0;
            }
            char[] chars = pre.toCharArray();
            TireNode node = root;
            int index = 0;
            for (int i = 0; i < chars.length; i++) {
                index = chars[i] - 'a';
                if (node.nexts[index] == null) {
                    return 0;
                }
                node = node.nexts[index];
            }
            return node.path;
        }

    }

测试用例

 public static void main(String[] args) {
        Trie trie = new Trie();
        trie.insert("abc");
        trie.insert("abd");
        trie.insert("abd");
        trie.insert("bcd");
        trie.insert("bcdef");

        int bcdNum = trie.prefixNumber("bcd");
        System.out.println(bcdNum);
        int search1 = trie.search("ab");
        System.out.println(search1);
        int search2 = trie.search("abd");
        System.out.println(search2);
        trie.delete("abc");
        int search3 = trie.search("abc");
        System.out.println(search3);
    }

结果输出

0
2
0

结语

如果以上文章对您有一点点帮助，希望您不要吝啬的点个赞加个关注，您每一次小小的举动都是我坚持写作的不懈动力！ღ( ´･ᴗ･` )