欧拉函数

https://oi-wiki.org/math/number-theory/euler/

定义

即 1 ~ n 中和 n 互质的数字个数。

Q：怎么判断两个数是互质的？
A：两个数的 最大公约数为1。（比如 1 和 1 就是互质的）

性质

求 $\phi (n)$：

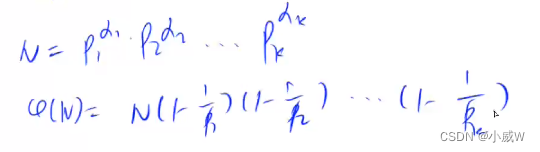
即 先完成质因数分解，然后按公式计算。

例题列表

873. 欧拉函数（使用质因数分解求一个数的欧拉函数）

https://www.acwing.com/activity/content/problem/content/942/

原理讲解（公式推导）⭐

使用 容斥原理 计算出 ——

1 ~ N 中所有质数的个数是：

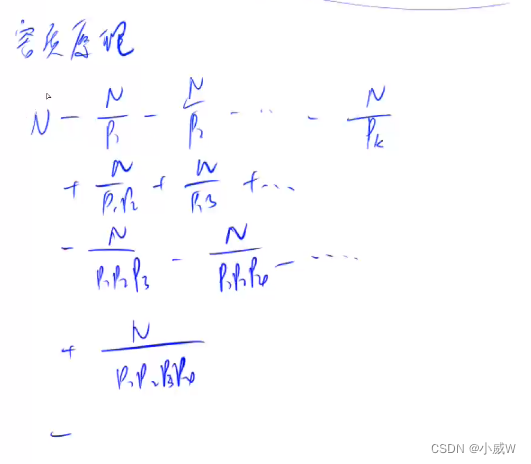
化简之后就是公式了。

解法代码

记住公式，
使用质因数分解求出 n 的所有的质因子。
使用所有质因子按照公式计算 n 的欧拉函数。（题目中也给出了公式）

import java.util.*;

public class Main {
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        while (n-- != 0) {
            System.out.println(euler(sc.nextInt()));
        }
    }

    static long euler(int n) {
        long res = n;
        for (int i = 2; i <= n / i; ++i) {
            if (n % i == 0) {
                while (n % i == 0) n /= i;
                res = res * (i - 1) / i;
            }
        }
        if (n > 1) res = res * (n - 1) / n;
        return res;
    }
}

874. 筛法求欧拉函数（求 1 ~ n 中所有数字的欧拉函数）⭐

https://www.acwing.com/activity/content/problem/content/943/

在欧氏筛质数的过程中计算欧拉函数。

使用到的一些欧拉函数的性质：

1. 质数 $x$ 的欧拉函数是 $x-1$。
2. 对于 $t=p[j]\ast i$。当 $i$ 时，即 $p[j]$ 也是 $i$ 的质因子，则 $t=i\ast p[j]$ 的质因子和 $i$ 的质因子一样，因此 $euler[t]=p[j]\ast euler[i]$。
3. 对于 $t=p[j]\ast i$。当 $i$ 时，即 $p[j]$ 不是 $i$ 的质因子，则 $t=i\ast p[j]$ 的质因子比 $i$ 的质因子多了一个 $p[j]$，因此 $euler[t]=p[j]\ast euler[i]\ast (1-1/p[j])=(p[j]-1)\ast euler[i]$。

import java.util.*;

public class Main {
    final static int N = 1000001;
    static int cnt = 0;
    static int[] primes = new int[N], euler = new int[N];
    static boolean[] st = new boolean[N];       // 是否被筛掉了

    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();

        euler[1] = 1;                           // 初始化欧拉数组
        // 欧氏筛质数
        for (int i = 2; i <= n; ++i) {
            if (!st[i]) {                       // 如果 i 没有被筛掉，是质数
                primes[cnt++] = i;
                euler[i] = i - 1;               // 质数的 x 的欧拉函数是 x - 1 (去掉它本身)
            }
            // 筛掉所有 primes[j] 的 i 倍
            for (int j = 0; primes[j] <= n / i; ++j) {
                int t = primes[j] * i;
                st[t] =true;
                if (i % primes[j] == 0) {
                    euler[t] = euler[i] * primes[j];	// t和i的质因子一样
                    break;
                }
                euler[t] = euler[i] * (primes[j] - 1);	// t的质因子比i多了一个p[j]
            }
        }

        long ans = 0;                           // 答案会超 int，所以使用 long
        for (int i = 1; i <= n; ++i) {
            ans += euler[i];
        }
        System.out.println(ans);
    }
}

在 欧式筛的过程中，利用上面提到的一些性质来筛出 1 ~ n 的所有欧拉函数。