【每日一题Day274】LC42接雨水

【每日一题Day274】LC42接雨水 | 单调栈

news2024/11/23 7:12:35

接雨水【LC42】[面试常见]

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

按列求贡献：枚举

首先确定按行计算雨水，还是按列确定雨水

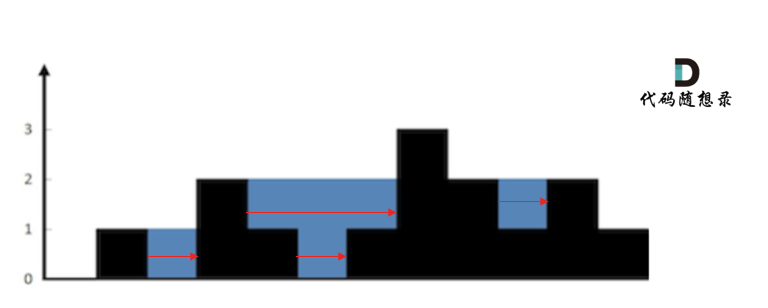
按行计算：
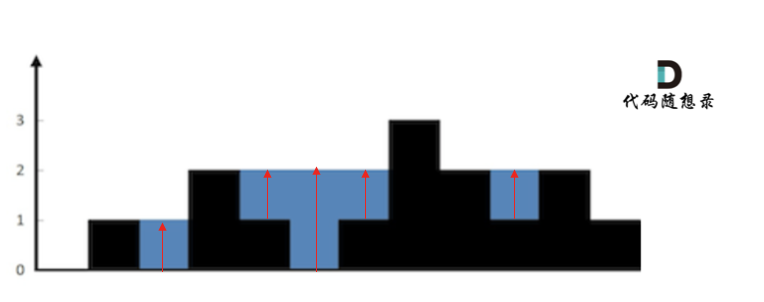
按列计算：找每个柱子左右两边第一个大于该柱子高度的柱子

第一列和最后一列不能容纳雨水，其他列可以容纳的雨水量宽度固定为1，高度取决于min（该列左侧最高的柱子，该列右侧最高的柱子）- 该列的高度

代码

class Solution {
    public int trap(int[] height) {
        int res = 0;
        int lens = height.length;
        for (int i = 1; i < lens - 1; i++){
            int maxL = height[i];
            int maxR = height[i];// Math.min(maxL,maxR) - height[i] 一定大于0
            for (int j = 0; j < i; j++){
                maxL = Math.max(maxL,height[j]);
            }
            for (int k = i + 1; k < lens; k++){
                maxR = Math.max(maxR,height[k]);
            }
            res += Math.min(maxL,maxR) - height[i];
        }
        return res;
    }
}

class Solution {
    public int trap(int[] height) {
        int res = 0;
        int lens = height.length;
        for (int i = 1; i < lens - 1; i++){
            int maxL = 0;
            int maxR = 0;// h可能小于0
            for (int j = 0; j < i; j++){
                maxL = Math.max(maxL,height[j]);
            }
            for (int k = i + 1; k < lens; k++){
                maxR = Math.max(maxR,height[k]);
            }
            int h = Math.min(maxL,maxR) - height[i];
            if (h > 0){
                res += h;
            }
        }
        return res;
    }
}

复杂度
- 时间复杂度： $O(n^2)$
- 空间复杂度： $O (1)$

按列求贡献：动态规划

使用dp数组记录，每列左边柱子的最高高度和右边柱子的最高高度

class Solution {
    public int trap(int[] height) {
        int res = 0;
        int lens = height.length;
        int[] maxL = new int[lens];
        maxL[0] = height[0];
        int[] maxR = new int[lens];
        maxR[lens-1] = height[lens-1];
        for (int i = 1; i < lens; i++){
            maxL[i] = Math.max(maxL[i-1],height[i]);
        }
        for (int i = lens - 2; i >= 0; i--){
            maxR[i] = Math.max(maxR[i+1],height[i]);
        }
        for (int i = 1; i < lens-1; i++){
            res += Math.min(maxL[i],maxR[i]) - height[i];
        }
        return res;
    }
}

复杂度
- 时间复杂度： $O (n)$
- 空间复杂度： $O (n)$

按行求：单调栈

思路

使用单调递增栈记录，凹槽处的左边高度和右边高度，按行计算雨水体积。当当前高度大于栈顶元素时，计算雨水体积，高度为左右边高度较小值-凹槽高度，宽度为右边下标-左边下标-1
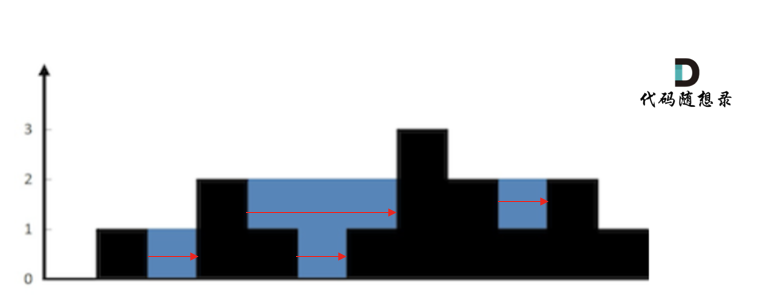
单调栈里元素是递增呢？还是递减呢？

递增，注意一下顺序为从栈头到栈底的顺序
使用单调栈主要有三个判断条件。
- 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
  
  直接把这个元素压入栈
- 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
  
  入栈或者不入栈，之前元素弹出或者不弹出不影响结果，（因为遇到相同高度的柱子时，需要使用最右边的柱子以及最左边的柱子计算宽度，左边为相同高度柱子时，计算结果为0）
- 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
  
  此时出现凹槽，可以容纳雨水，计算雨水容量，再入栈
  - 取栈顶元素，将栈顶元素弹出，下标即为mid，这个位置为凹槽的底部
  - 再取栈顶元素，下标为st.peekFirst()，这个位置为凹槽的左侧
  - 当前遍历元素为凹槽的右边位置，下标为i
  - 雨水高度为min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
    
    int h = min(height[st.peekFirst()], height[i]) - height[mid];
  - 雨水宽度为凹槽右边的下标 - 凹槽左边的下标 - 1
    
    int w = i - st.peekFirst() - 1 ;
  - 雨水的体积为h * w

实现

2023/7/23

class Solution {
    public int trap(int[] height) {
        
        // 贡献：每个位置能积累的水量为min(左边最大，右边最大)-柱子高度
        // int n = height.length;
        // int[] left = new int[n], right = new int[n];
        // for (int i = 0; i < n - 1; i++){
        //     left[i + 1] = Math.max(left[i], height[i]);
        //     right[n - i - 2] = Math.max(right[n - i - 1], height[n - i - 1]);
        // }
        // int res = 0;
        // for (int i = 0; i < n; i++){
        //     res += Math.max(Math.min(right[i], left[i]) - height[i], 0);
        // }
        // return res;
        // 单调递增栈【栈顶->栈底】：遇到大于栈顶的柱子，弹出计算雨水量；
        Deque<Integer> st = new LinkedList<>();
        int n = height.length, res = 0;
        for (int i = 0; i < n; i++){
            while (!st.isEmpty() && height[st.peekLast()] <= height[i]){
                int mid = st.pollLast();
                if (st.isEmpty()){
                    break;
                }
                int left = st.peekLast();
                int w = i - left - 1;
                int h = Math.min(height[left], height[i]) - height[mid];
                res += w * h;
            }
            st.addLast(i);
        }
        return res;

    }
}