一、说明
如果您想了解更多关于PCA和ZCA之间的区别,请查看我之前基于numpy的帖子:
PCA 美白与 ZCA 美白:2D 视觉效果
白化数据的过程包括转换,使得转换后的数据具有单位矩阵作为...
towardsdatascience.com
二、各类降维模型概念
2.1 PCA : 主成分分析
- PCA是一种无监督线性降维技术,旨在找到一组新的正交变量,以捕获数据中最重要的可变性来源。
- 它广泛用于特征提取和数据压缩,可用于探索性数据分析或作为机器学习算法的预处理步骤。
- 生成的分量按其解释的方差量进行排名,可用于可视化和解释数据,以及用于聚类或分类任务。
2.2 LDA : 线性判别分析
- LDA 是一种受监督的线性降维技术,旨在找到一组新的变量,以最大化类之间的分离,同时最小化每个类内的变化。
- 它广泛用于特征提取和分类,可用于降低数据的维数,同时保留类之间的判别信息。
- 生成的组件按其判别能力进行排名,可用于可视化和解释数据,以及用于分类或回归任务。
2.3 ICA : 独立成分分析
- ICA是一种无监督线性降维技术,旨在找到一组统计上独立且非高斯的新变量。
- 它广泛用于信号处理和源分离,并可用于提取数据中无法通过其他技术访问的潜在可变性源。
- 生成的组件按其独立性进行排名,可用于可视化和解释数据,以及用于聚类或分类任务。
三、鸢尾花数据集上的结果
让我们使用 sklearn 比较他们在著名的鸢尾花数据集上的结果。首先,让我们在 4 个数值特征中的每一个上使用配对图绘制鸢尾花数据集,并将颜色作为分类特征:
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
# Load the iris dataset
iris = load_iris()
data = iris.data
target = iris.target
target_names = iris.target_names
# Convert the iris dataset into a pandas DataFrame
iris_df = sns.load_dataset('iris')
iris_df['target'] = target
# Generate the pairplot∑
sns.pairplot(data=iris_df, hue='target', palette=['navy', 'turquoise', 'darkorange'], markers=['o', 's', 'D'],
plot_kws=dict(s=25, alpha=0.8, edgecolor='none'), diag_kws=dict(alpha=0.8, edgecolor='none'))
# Set the title and adjust plot spacing
plt.suptitle('Iris Pairplot')
plt.subplots_adjust(top=0.92)
plt.show()
图片来源:虹膜数据集对图
现在,我们可以计算每个变换并绘制结果。请注意,我们只使用 2 个组件,因为 LDA 最多需要 (N-1) 个组件,其中 N 是类别的数量(这里等于 3,因为有 3 种类型的鸢尾花)。
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA, FastICA
import matplotlib.pyplot as plt
# Load the Iris dataset
iris = load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names
# Standardize the data
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# Apply LDA with 2 components
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X_std, y)
# Apply PCA with 2 components
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_std)
# Apply ICA with 2 components
ica = FastICA(n_components=2)
X_ica = ica.fit_transform(X_std)
# Plot the results
plt.figure(figsize=(15, 5))
plt.subplot(1, 3, 1)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):
plt.scatter(X_lda[y == target, 0], X_lda[y == target, 1], color=color, alpha=.8, lw=2,
label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('LDA')
plt.xlabel('LD1')
plt.ylabel('LD2')
plt.subplot(1, 3, 2)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):
plt.scatter(X_pca[y == target, 0], X_pca[y == target, 1], color=color, alpha=.8, lw=2,
label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('PCA')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.subplot(1, 3, 3)
for target, color in zip(range(len(target_names)), ['navy', 'turquoise', 'darkorange']):
plt.scatter(X_ica[y == target, 0], X_ica[y == target, 1], color=color, alpha=.8, lw=2,
label=target_names[target])
plt.legend(loc='best', shadow=False, scatterpoints=1)
plt.title('ICA')
plt.xlabel('IC1')
plt.ylabel('IC2')
plt.show()This code loads the Iris dataset, applies LDA, PCA, and ICA with 2 components each, and then plots the results using different colors for each class.
请注意,在应用 PCA、ICA 或 LDA 之前标准化数据通常是一种很好的做法。标准化很重要,因为这些技术对输入要素的比例很敏感。标准化数据可确保每个要素的均值为 0,标准差为 1,这会将所有要素置于同一尺度上,并避免一个要素凌驾于其他要素之上。
由于LDA是一种监督降维技术,因此它将类标签作为输入。相比之下,PCA和ICA是无监督技术,这意味着它们只使用输入数据,而不考虑类标签。
LDA 的结果可以解释为将数据投影到最大化类分离的空间上,而 PCA 和 ICA 的结果可以解释为将数据投影到空间上,该空间分别捕获最重要的可变性或独立性来源。

图片来源:虹膜数据集上LDA,PCA和ICA的比较
请注意,ICA仍然显示类别之间的分离,尽管不是其目的:这是因为类别已经在输入数据集中进行了相当排序。
让我们把LDA放在一边,专注于PCA和ICA之间的差异 - 因为LDA是一种监督技术,专注于分离类别并强制实施最大的组件,而PCA和ICA专注于创建一个与输入矩阵形状相同的新矩阵。
让我们看看 PCA 和 ICA 的 4 个组件的输出:


左:PCA的对图/右:ICA的对图(图片由作者提供)
让我们也比较每个转换数据的相关矩阵:请注意,这两种方法都会导致不相关的向量(换句话说,转换后的数据特征是正交的)。这是因为它是PCA算法中的一个约束 - 每个新向量必须与以前的向量正交 - 并且是ICA算法的结果 - 这意味着原始数据集是已经混合在一起的独立信号,必须重建。


左:ICA的相关热图/右:PCA的相关热图(图片由作者提供)
所以PCA和ICA似乎给出了具有相似性质的结果:这是因为以下2个原因:
- 独立性在两种算法中都“编码”
- 鸢尾花数据集表现出分离良好的类
这就是为什么我们需要另一个更适合ICA的例子。
四、另一个例子:
让我们看另一个例子:我们首先生成一个合成数据集,其中包含两个独立的源,一个正弦波和一个方波,它们作为线性组合混合在一起以创建混合信号。
实际的、真实的、独立的信号如下:

它们混合在一起,作为 2 个线性组合:

让我们看看PCA和ICA在这个新数据集上的表现:
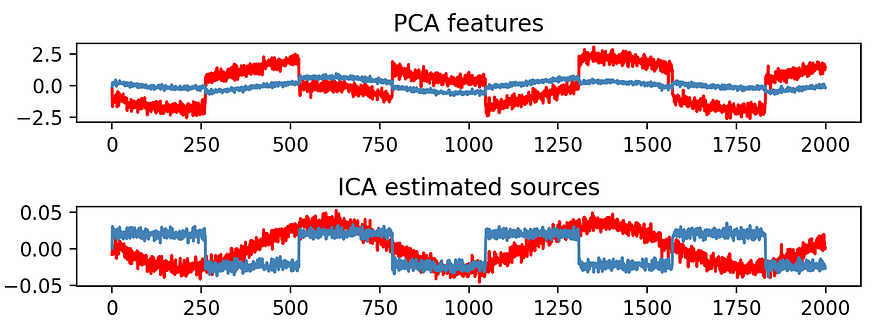
注意PCA如何创建一个新组件,该组件表现出很大的方差,作为输入的线性组合,但这绝对与原始数据不匹配:这确实不是PCA的目的。
相反,ICA在恢复原始数据集方面表现非常好,与方差组成无关。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import FastICA
# Generate a synthetic dataset with two independent sources
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)
s1 = np.sin(2 * time) # Source 1: sine wave
s2 = np.sign(np.sin(3 * time)) # Source 2: square wave
S = np.c_[s1, s2]
S += 0.2 * np.random.normal(size=S.shape) # Add noise to the sources
S /= S.std(axis=0) # Standardize the sources
# Mix the sources together to create a mixed signal
A = np.array([[0.5, 0.5], [0.2, 0.8]]) # Mixing matrix
X = np.dot(S, A.T) # Mixed signal
# Standardize the data
X = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
# Use PCA to reduce the dimensionality of the data
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
# Use ICA to separate the sources from the mixed signal
ica = FastICA(n_components=2)
X_ica = ica.fit_transform(X) # Estimated sources
# Plot the results
plt.figure()
models = [X, S, X_pca, X_ica]
names = ['Observations (mixed signal)',
'True Sources',
'PCA features', 'ICA estimated sources']
colors = ['red', 'steelblue']
for ii, (model, name) in enumerate(zip(models, names), 1):
plt.subplot(4, 1, ii)
plt.title(name)
for sig, color in zip(model.T, colors):
plt.plot(sig, color=color)
plt.tight_layout()
plt.show()五、结论
PCA、LDA 和 ICA 算法可能看起来像是彼此的自定义版本,但它们实际上没有相同的目的。总结一下:
- PCA旨在创建保持输入最大方差的新组件
- LDA 旨在创建基于分类特征分隔集群的新组件
- ICA 旨在检索在输入数据集中以线性组合混合在一起的原始要素
希望您更好地了解这些算法之间的差异,并能够在将来快速识别您需要的算法。