226. 翻转二叉树
文章目录
- [226. 翻转二叉树](https://leetcode.cn/problems/invert-binary-tree/)
- 一、题目
- 二、题解
- 方法一:层序遍历迭代
- 方法二:前序遍历(递归)
- 方法三:中序遍历(递归)
- 方法四:后序遍历(递归)
- 方法五:前序遍历(迭代)
- 方法六:迭代统一写法
一、题目
给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。
示例 1:
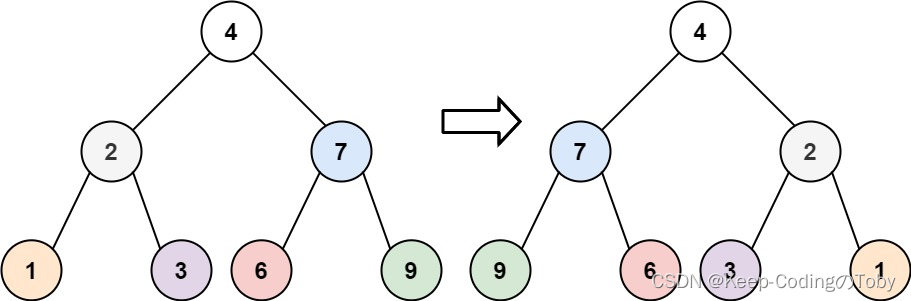
输入:root = [4,2,7,1,3,6,9]
输出:[4,7,2,9,6,3,1]
示例 2:
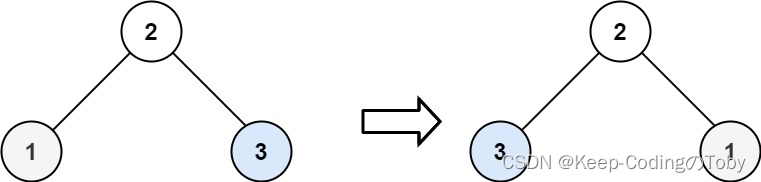
输入:root = [2,1,3]
输出:[2,3,1]
示例 3:
输入:root = []
输出:[]
二、题解
方法一:层序遍历迭代
算法思路:
-
翻转一棵树,就是将树中所有节点的左右子节点进行交换。
-
可以采用广度优先搜索的方式遍历这棵树,依次翻转每个节点的左右子节点。
-
使用双端队列作为辅助存储结构,以队列的方式维护待遍历的节点。
具体实现:
-
定义双端队列deq,用于存储待遍历的节点。
-
从根节点开始,将根节点入队到deq。
-
开始遍历:
-
记录当前队列大小size,用于控制每层遍历次数
-
循环size次,每次队头出队一个节点:
-
交换该节点的左右子节点指针
-
如果左右子节点不为空,加入deq继续遍历(注意是先push右节点,然后push左节点)
-
-
-
遍历完成后,整棵树的节点都被翻转过
-
返回根节点
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) return root;
deque<TreeNode*> deq;
deq.push_back(root);
while(!deq.empty()){
int size = deq.size();
for(int i = 0; i < size; i++){
TreeNode *node = deq.front();
deq.pop_front();
swap(node->left,node->right);
/*TreeNode *temp = node->right;
node->right = node->left;
node->left = temp;*/
if(node->right) deq.push_back(node->right);
if(node->left) deq.push_back(node->left);
}
}
return root;
}
};
算法分析:
-
时间复杂度 O(N):遍历了树中的所有节点
-
空间复杂度 O(N):队列中最多存储树的所有节点
方法二:前序遍历(递归)
算法思路:
-
二叉树的翻转可以使用递归的方法实现。
-
思路是,对树的每个节点,交换它的左右子节点,然后递归地对它的左右子节点进行翻转。
-
通过递归,可以一层一层地进行节点交换,直到叶子节点,实现整棵树的翻转。
具体实现:
-
定义递归函数invertTree,输入根节点root。
-
在函数内:
-
交换root的左右子节点
-
递归调用invertTree,输入root的左子节点
-
递归调用invertTree,输入root的右子节点
-
-
当递归到叶子节点时,左右子节点为空,直接返回。
-
通过递归返回,整棵树的节点都被交换过了。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) return root;
swap(root->left,root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
算法分析:
-
时间复杂度 O(N):需要递归遍历树的所有节点。
-
空间复杂度 O(H):递归函数在递归调用栈上需要O(H)空间,H为树高。
方法三:中序遍历(递归)
具体实现:
-
定义递归函数invertTree,输入根节点root。
-
在函数内:
-
首先递归翻转左子树
-
然后交换当前root节点的左右子树
-
最后递归翻转右子树(已经交换后的左子树)
-
-
通过递归先序遍历的流程,每个节点都会被翻转一次。
-
当遍历到null时,直接返回,递归终止。
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) return root;
invertTree(root->left);
swap(root->left,root->right);
invertTree(root->left);
return root;
}
};
算法分析:
-
时间复杂度 O(N):遍历树的所有节点。
-
空间复杂度 O(H):递归栈空间为树高。
方法四:后序遍历(递归)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == nullptr) return root;
invertTree(root->left);
invertTree(root->right);
swap(root->left,root->right);
return root;
}
};
方法五:前序遍历(迭代)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root == nullptr) return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
st.pop();
swap(node->left,node->right);
if(node->right) st.push(node->right);
if(node->left) st.push(node->left);
}
return root;
}
};
方法六:迭代统一写法
前序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root == nullptr) return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != NULL){
st.pop();
if(node->right) st.push(node->right); //右
if(node->left) st.push(node->left); //左
st.push(node); //中
st.push(NULL);
}else{
st.pop();
node = st.top();
st.pop();
swap(node->left,node->right);
}
}
return root;
}
};
中序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root == nullptr) return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != NULL){
st.pop();
if(node->right) st.push(node->right); //右
st.push(node); //中
st.push(NULL);
if(node->left) st.push(node->left); //左
}else{
st.pop();
node = st.top();
st.pop();
swap(node->left,node->right);
}
}
return root;
}
};
后序遍历
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
stack<TreeNode*> st;
if(root == nullptr) return root;
st.push(root);
while(!st.empty()){
TreeNode* node = st.top();
if(node != NULL){
st.pop();
st.push(node); //中
st.push(NULL);
if(node->right) st.push(node->right); //右
if(node->left) st.push(node->left); //左
}else{
st.pop();
node = st.top();
st.pop();
swap(node->left,node->right);
}
}
return root;
}
};