文章目录
- 求最短路算法总览
- Dijkstra
- 朴素 Dijkstra 算法(⭐原理讲解!⭐重要!)(用于稠密图)
- 例题:849. Dijkstra求最短路 I
- 代码1——使用邻接表
- 代码2——使用邻接矩阵
- 补充:稠密图和稀疏图 & 邻接矩阵和邻接表
- 堆优化版Dijkstra算法(⭐原理讲解!⭐重要!)用于稀疏图
- 例题:850. Dijkstra求最短路 II
- bellman-ford
- 例题:853. 有边数限制的最短路
- 为什么需要对 dis 数组进行备份?
- spfa算法(bellman-ford 算法的优化)
- 例题:851. spfa求最短路
- 例题:852. spfa判断负环
- Floyd(很暴力的三重循环)
- 例题:854. Floyd求最短路
求最短路算法总览
关于最短路可见:https://oi-wiki.org/graph/shortest-path/

无向图 是一种 特殊的 有向图。(所以上面的知识地图上没有区分边有向还是无向)
关于存储:稠密图用邻接矩阵,稀疏图用邻接表。
朴素Dijkstra 和 堆优化Dijkstra算法的 选择就在于图 是 稠密的还是稀疏的。
Dijkstra
朴素 Dijkstra 算法(⭐原理讲解!⭐重要!)(用于稠密图)
算法步骤:
有一个集合 s 存储当前已经确定是最短距离的点。
- 初始化距离,dis[1] = 0, dis[i] = +∞
- for i: 1 ~ n 。 (每次循环确定一个点到起点的最短距离,这样 n 次循环就可以确定 n 个点的最短距离)
找到不在 s 中的 距离最近的点 t,将其放入 s 中。
用 t 来更新其它所有点的距离(检查所有从 t 出发可以到达的点 x,是否有 dis[x] > dis[t] + w)

例题:849. Dijkstra求最短路 I
https://www.acwing.com/activity/content/problem/content/918/
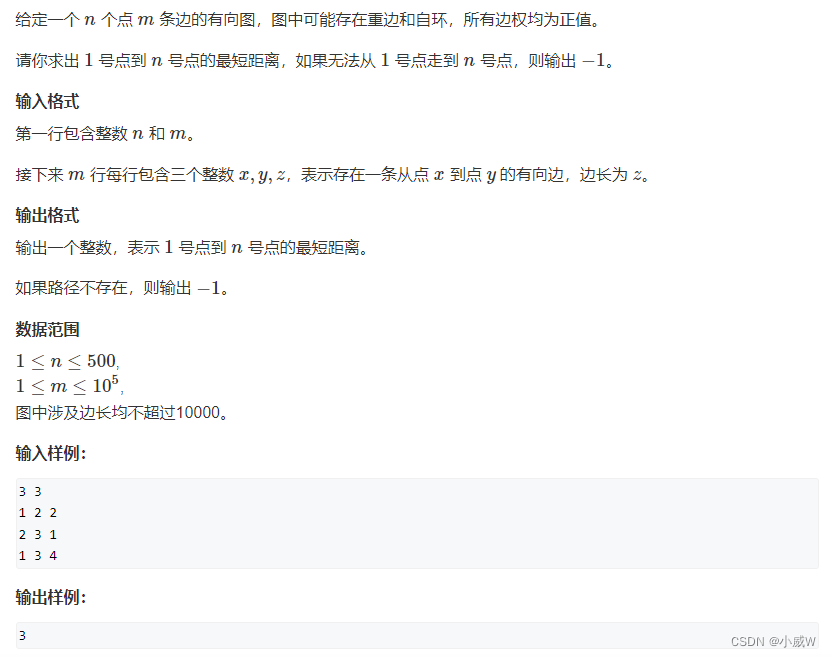
注意图是有向图,图中可能存在重边和自环,所有边权为正值。
求从 1 号点到 n 号点 的最短距离。
按照朴素 Dijkstra 算法的原理,每次用当前不在 s 中的最短距离节点 t 更新其它所有 t 可以到达的下一个节点,重复这个过程 n 次就可以确定 n 个节点的最短距离。
代码1——使用邻接表
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
// 建图
List<int[]>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<>());
for (int i = 0; i < m; ++i) {
int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();
g[x].add(new int[]{y, z});
}
// 初始化距离
int[] dis = new int[n + 1];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[1] = 0;
boolean[] st = new boolean[n + 1];
for (int i = 1; i < n; ++i) {
int t = -1;
// 找到当前不在 s 中的最短距离 t 的位置
for (int j = 1; j <= n; ++j) {
if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;
}
if (t == n) break; // 当前离得最近的就是 n 了,直接返回
st[t] = true;
// 使用 t 更新所有从 t 出发可以达到的下一个节点
for (int[] y: g[t]) dis[y[0]] = Math.min(dis[y[0]], dis[t] + y[1]);
}
if (dis[n] == Integer.MAX_VALUE) System.out.println("-1");
else System.out.println(dis[n]);
}
}
代码2——使用邻接矩阵
从题目中可以看出是稠密图,所以使用邻接矩阵效率会更高一些。
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
// 建图 g[i][j]表示从i到j的距离
int[][] g = new int[n + 1][n + 1];
for (int[] ints : g) Arrays.fill(ints, 0x3f3f3f3f);
for (int i = 0; i < m; ++i) {
int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();
g[x][y] = Math.min(g[x][y], z);
}
// 初始化各个点到起始点的距离
int[] dis = new int[n + 1];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[1] = 0;
boolean[] st = new boolean[n + 1];
for (int i = 1; i < n; ++i) {
int t = -1;
// 找到当前不在 s 中的最短距离 t 的位置
for (int j = 1; j <= n; ++j) {
if (!st[j] && (t == -1 || dis[j] < dis[t])) t = j;
}
if (t == n) break; // 当前离得最近的就是 n 了,直接返回
st[t] = true;
// 使用 t 更新所有从 t 出发可以达到的下一个节点
for (int j = 1; j <= n; ++j) {
dis[j] = Math.min(dis[j], dis[t] + g[t][j]);
}
}
if (dis[n] == 0x3f3f3f3f) System.out.println("-1");
else System.out.println(dis[n]);
}
}
补充:稠密图和稀疏图 & 邻接矩阵和邻接表

总结一下:
邻接矩阵的空间复杂度为 O ( n 2 ) O(n^2) O(n2),邻接表的空间复杂度为 O ( n + m ) O(n + m) O(n+m),其中 n 是图中节点的数量,m 是边的数量。
Q:如何判断什么时候是稠密的?
A:当
m
m
m 接近最大可能边数
n
∗
(
n
−
1
)
/
2
n * (n - 1)/2
n∗(n−1)/2 时,那么图通常被视为稠密的。
堆优化版Dijkstra算法(⭐原理讲解!⭐重要!)用于稀疏图
如果是一个稀疏图,
O
(
n
2
)
O(n^2)
O(n2) 的朴素 Dijkstra 算法可能会很慢,因此出现了堆优化版本的 Dijkstra 算法。

用堆来存储所有点到起点的最短距离,就可以减小整个算法的时间复杂度。
用 t 更新其它点的距离,因为有 m 条边,所以这个操作是 m 次,每次的时间复杂度是 logn,因此一共是 m ∗ log n m*\log{n} m∗logn。 (所以 m 比较小时,即稀疏图,使用堆优化效果更好)
其实就是用堆来优化了每次找当前和起始点最近的点的过程。(朴素的需要枚举 n)
例题:850. Dijkstra求最短路 II
https://www.acwing.com/activity/content/problem/content/919/
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
// 建图
List<int[]>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<int[]>());
for (int i = 0; i < m; ++i) {
int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();
g[x].add(new int[]{y, z});
}
//
int[] dis = new int[n + 1];
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
boolean[] st = new boolean[n + 1];
// 按照各个节点与初始节点之间距离 从小到大 排序
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> a[1] - b[1]);
pq.offer(new int[]{1, 0});
while (!pq.isEmpty()) {
int[] cur = pq.poll();
int x = cur[0], d = cur[1];
if (st[x]) continue; // 检查这个节点是否已经用来更新过了
st[x] = true;
// 只要被当前节点更新了就放入优先队列中
for (int[] y: g[x]) { // 这个循环最多被执行 m 次(因为有 m 条边)
if (dis[y[0]] > d + y[1]) {
dis[y[0]] = d + y[1];
pq.offer(new int[]{y[0], dis[y[0]]});
}
}
}
System.out.println(dis[n] == 0x3f3f3f3f? -1: dis[n]);;
}
}
bellman-ford
枚举 n 次:
每次 循环所有边 a, b, w
dis[b] = min(dis[b], dis[a] + w)
循环完之后, 所有节点会满足 dis[b] <= dis[a] + w。

对于 n 次循环中的第 k 次循环,求出的是 : 从 起点走 不超过 k 条边 的最短距离。
因此 如果第 n 次循环时有更新,说明图中存在负环。
例题:853. 有边数限制的最短路
https://www.acwing.com/problem/content/description/855/

注意! : 如果有负权回路,那么最短路就一定不存在了!
bellman-ford 算法可以判断出 图中是否存在负权回路。(但是一般使用 spfa 来判断是否有负环)
Q:这道题为什么必须使用 bellman-ford 算法?
A:因为限制了最多经过 k 条边,即存在边数限制。
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt(), k = scanner.nextInt();
// 存储所有边
int[][] edges = new int[m][3];
for (int i = 0; i < m; ++i) {
edges[i][0] = scanner.nextInt();
edges[i][1] = scanner.nextInt();
edges[i][2] = scanner.nextInt();
}
int[] dis = new int[n + 1], last;
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
// 限制 k 次。 (k 次就表示最多经过 k 条边)
for (int i = 0; i < k; ++i) {
last = Arrays.copyOf(dis, n + 1); // 将dis数组先备份一下
for (int j = 0; j < m; ++j) { // 枚举所有边
dis[edges[j][1]] = Math.min(dis[edges[j][1]], last[edges[j][0]] + edges[j][2]);
}
}
// 因为存在负权边,而本题的数据范围最多减 500 * 10000。所以和 0x3f3f3f3f/2 比较大小
System.out.println(dis[n] > 0x3f3f3f3f / 2? "impossible": dis[n]);
}
}
为什么需要对 dis 数组进行备份?
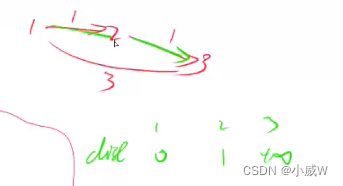
因为如果不备份的话可能会发生串联,为了避免串联,每次更新时只用上一次的结果。
比如上图,在第一次循环中 2 的 dis 被更新成了 1,如果不使用备份的话,那么 3 的 dis 会被接着更新为 2,但这并不是我们所期望的, 3 的 dis 被更新成 2 应该是在第 2 次循环时才会发生的事情。
spfa算法(bellman-ford 算法的优化)
相当于对 bellman-ford 算法做了一个优化。
bellman-ford 在每次循环中枚举了所有边,但实际上有些边并不会对松弛有作用,所以 spfa 就是从这一点进行了优化。
(使用队列宽搜进行优化)。
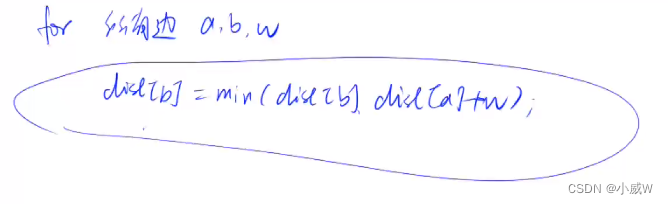
从公式 d i s [ b ] = m i n ( d i s [ b ] , d i s [ a ] + w ) dis[b] = min(dis[b], dis[a] + w) dis[b]=min(dis[b],dis[a]+w) 可以看出,只有当 d i s [ a ] dis[a] dis[a] 变小了,这条边才有可能让 d i s [ b ] dis[b] dis[b] 跟着变小。
算法步骤:

基本思想:只有我变小了,我后面的人才会跟着变小。
队列里面存的是待更新的点,就是等着用来更新其它点的点。
例题:851. spfa求最短路
https://www.acwing.com/activity/content/problem/content/920/
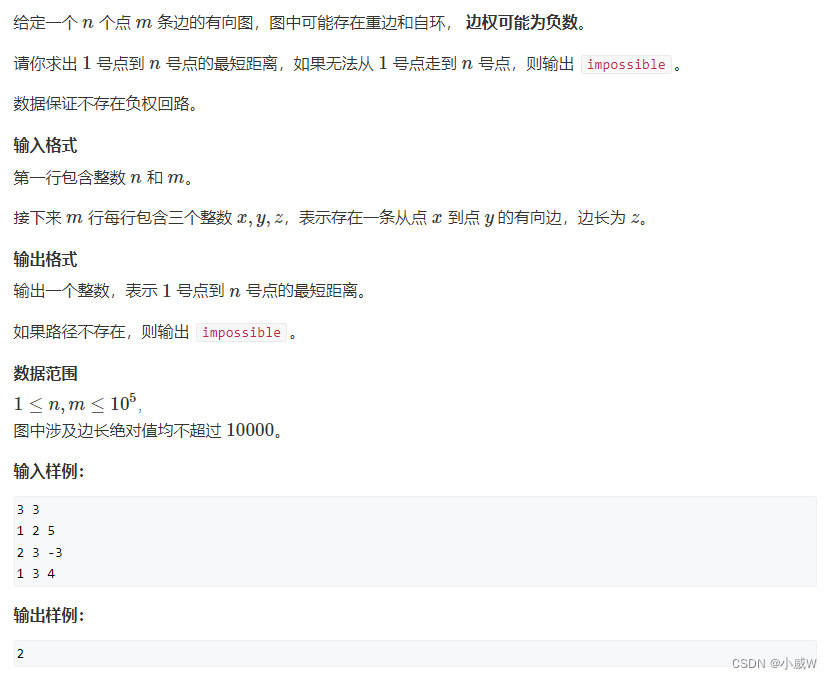
这一题的数据保证了图中不存在负环。
代码中不再是 n 次循环嵌套 m 次循环的 bellman-ford 算法了,
而是一个队列维护可以用来更新其它节点的节点队列,初始时放入起始节点 1,其余时间每次取出队首的节点即可。
取出一个节点后,枚举它影响的所有其它节点即可,如果其它节点被影响了,就表示可以把这个被影响的节点放入队列中,(不过放进队列之前要先判断一下是否已经在队列中了,防止重复更新)。
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
// 使用邻接表存储
List<int[]>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<int[]>());
for (int i = 0; i < m; ++i) {
g[scanner.nextInt()].add(new int[]{scanner.nextInt(), scanner.nextInt()});
}
// 初始化距离、队列、是否在队列里的状态
int[] dis = new int[n + 1];
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
Queue<Integer> q = new LinkedList<Integer>();
q.offer(1);
boolean[] st = new boolean[n + 1];
st[1] = true;
while (!q.isEmpty()) {
int t = q.poll();
st[t] = false;
for (int[] y: g[t]) {
int j = y[0], w = y[1];
if (dis[j] > dis[t] + w) {
dis[j] = dis[t] + w;
// 由于 j 变小了,所以它可以被更新,可以放入队列中
// 但是放进去之前要先判断已经是否已经在队列中了,防止重复放置
if (!st[j]) {
q.offer(j);
st[j] = true;
}
}
}
}
System.out.println(dis[n] == 0x3f3f3f3f? "impossible": dis[n]);
}
}
例题:852. spfa判断负环
https://www.acwing.com/problem/content/description/854/
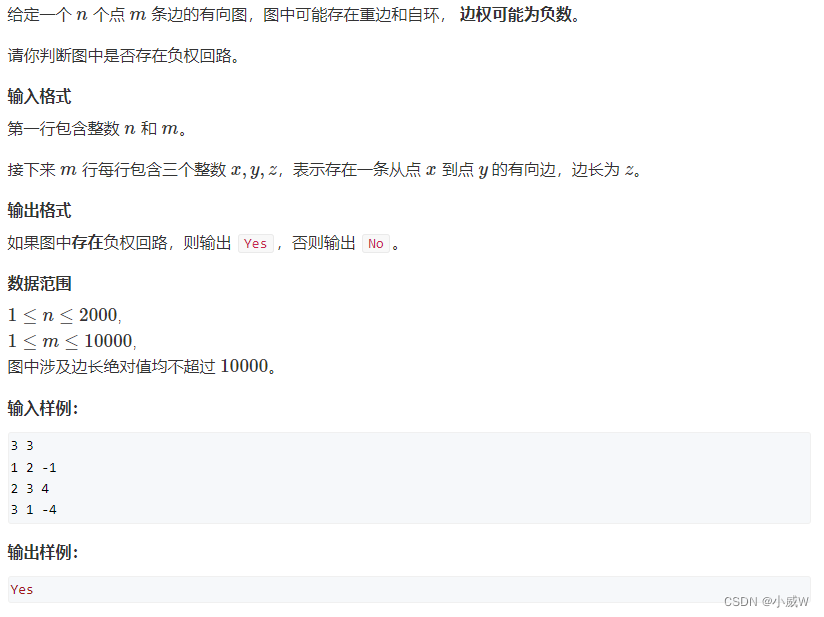
跟 bellman-ford 算法判断负环的思路差不多,在更新 dis 数组的同时,维护一个 cnt 数组,cnt[x] 表示当前这个最短路的经过的边数。
每次更新 dis[x] 的时候,就把 cnt[x] 更新成 cnt[t] + 1。(因为 x 是从节点 t 更新过来的)。
如果在更新的过程中出现了 cnt[x] >= n,就表示至少经过了 n 条边,即至少经过了 n + 1 个点,这肯定是不合理的,说明存在负环。
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt();
// 使用邻接表存储
List<int[]>[] g = new ArrayList[n + 1];
Arrays.setAll(g, e -> new ArrayList<int[]>());
for (int i = 0; i < m; ++i) {
g[scanner.nextInt()].add(new int[]{scanner.nextInt(), scanner.nextInt()});
}
System.out.println(spfa(g, n)? "Yes": "No");
}
static boolean spfa(List<int[]>[] g, int n) {
// 初始化距离、队列、是否在队列里的状态
int[] dis = new int[n + 1], cnt = new int[n + 1];
Arrays.fill(dis, 0x3f3f3f3f);
dis[1] = 0;
boolean[] st = new boolean[n + 1];
Queue<Integer> q = new LinkedList<Integer>();
// 是判断是否存在负环,而不是只判断从1开始是否存在负环
for (int i = 1; i <= n; ++i) {
q.offer(i);
st[i] = true;
}
while (!q.isEmpty()) {
int t = q.poll();
st[t] = false;
for (int[] y: g[t]) {
int j = y[0], w = y[1];
if (dis[j] > dis[t] + w) {
dis[j] = dis[t] + w;
cnt[j] = cnt[t] + 1;
if (cnt[j] >= n) return true; // 表示有负环
// 由于 j 变小了,所以它可以被更新,可以放入队列中
// 但是放进去之前要先判断已经是否已经在队列中了,防止重复放置
if (!st[j]) {
q.offer(j);
st[j] = true;
}
}
}
}
return false; // false表示没有负环
}
}
Floyd(很暴力的三重循环)
https://oi-wiki.org/graph/shortest-path/#floyd-%E7%AE%97%E6%B3%95
用于求多源汇最短路。可以求任意两个结点之间的最短路。
使用邻接矩阵将原图存储下来,三重循环。
d[i][j]
for (int k = 1; k <= n; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
// 看看i直接到j更近还是 经过k之后更近
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
原理其实是基于:动态规划
例题:854. Floyd求最短路
https://www.acwing.com/problem/content/856/

题目数据保证了不存在负权回路。
同样要注意最后各个距离要和 INF / 2 比较而不是和 INF 比较,因为图中可能存在负权。
import java.util.*;
public class Main {
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(), m = scanner.nextInt(), t = scanner.nextInt(), INF = (int)1e9;
// 建图
int[][] g = new int[n + 1][n + 1];
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
if (i == j) g[i][j] = 0;
else g[i][j] = INF;
}
}
for (int i = 0; i < m; ++i) {
int x = scanner.nextInt(), y = scanner.nextInt(), z = scanner.nextInt();
g[x][y] = Math.min(g[x][y], z);
}
// 求多源最短路
for (int k = 1; k <= n; ++k) {
for (int i = 1; i <= n; ++i) {
for (int j = 1; j <= n; ++j) {
g[i][j] = Math.min(g[i][j], g[i][k] + g[k][j]);
}
}
}
// 回答询问
while (t-- != 0) {
int x = scanner.nextInt(), y = scanner.nextInt();
System.out.println(g[x][y] > INF / 2? "impossible": g[x][y]); // 由于有负权,所以和INF/2比较
}
}
}