实验五  分支限界法

01背包问题的分治限界法的实现

剪枝函数

限界函数

1.实验目的

1、理解分支限界法的剪枝搜索策略，掌握分支限界法的算法框架

2、设计并实现问题，掌握分支限界算法。

2.实验环境

java

3.问题描述

给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

4.复杂度

算法整体的时间复杂度主要由回溯操作的时间复杂度决定，在最坏情况下为O(2^n)。然而，在实际应用中，由于剪枝操作的存在，实际的分支数会远远小于2^n，因此算法的执行时间通常会有所缩减。

5.算法实现

package shiyan5;

import java.io.File;
import java.io.FileWriter;
import java.io.IOException;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.Scanner;

class Item {
    int weight;
    int value;
    double density; // 物品的单位价值（价值重量比）

    public Item(int weight, int value) {
        this.weight = weight;
        this.value = value;
        this.density = (double) value / weight;
    }
}

public class BranchAndBound {
    static List<Item> items;
    static int capacity;
    static int maxTotalValue;
    static List<Item> selectedItems;

    public static void main(String[] args) {
        readInputData("input.txt");
        branchAndBound();
        writeOutputData("output.txt");
    }

    private static void readInputData(String filename) {
        try {
            File file = new File(filename);
            Scanner scanner = new Scanner(file);

            int n = scanner.nextInt();
            capacity = scanner.nextInt();
            items = new ArrayList<>();

            for (int i = 0; i < n; i++) {
                int weight = scanner.nextInt();
                int value = scanner.nextInt();
                items.add(new Item(weight, value));
            }

            scanner.close();
        } catch (IOException e) {
            e.printStackTrace();
        }
    }

    private static void branchAndBound() {
        Collections.sort(items, (a, b) -> Double.compare(b.density, a.density)); // 按单位价值从大到小排序

        maxTotalValue = 0;
        selectedItems = new ArrayList<>();

        backtrack(0, 0, 0);

        // 按照物品的原始顺序排序
        Collections.sort(selectedItems, (a, b) -> Integer.compare(items.indexOf(a), items.indexOf(b)));
    }

    private static void backtrack(int level, int currentWeight, int currentValue) {
        if (level == items.size() || currentWeight == capacity) {
            if (currentValue > maxTotalValue) {
                maxTotalValue = currentValue;
                selectedItems.clear();
                for (int i = 0; i < level; i++) {
                    if (items.indexOf(items.get(i)) != -1) {
                        selectedItems.add(items.get(i));
                    }
                }
            }
            return;
        }

        if (currentWeight + items.get(level).weight <= capacity) {
            currentWeight += items.get(level).weight;
            currentValue += items.get(level).value;

            backtrack(level + 1, currentWeight, currentValue);

            currentWeight -= items.get(level).weight;
            currentValue -= items.get(level).value;
        }

        if (bound(level + 1, currentWeight, currentValue) > maxTotalValue) {
            backtrack(level + 1, currentWeight, currentValue);
        }
    }

    private static double bound(int level, int currentWeight, int currentValue) {
        double maxBound = currentValue;
        int currentLevel = level;
        int currentWeightSum = currentWeight;

        while (currentWeightSum < capacity && currentLevel < items.size()) {
            if (currentWeightSum + items.get(currentLevel).weight <= capacity) {
                currentWeightSum += items.get(currentLevel).weight;
                maxBound += items.get(currentLevel).value;
            } else {
                double remainingWeight = capacity - currentWeightSum;
                maxBound += (remainingWeight / items.get(currentLevel).weight) * items.get(currentLevel).value;
                break;
            }
            currentLevel++;
        }

        return maxBound;
    }

    private static void writeOutputData(String filename) {
        try {
            FileWriter writer = new FileWriter(filename);
            writer.write("背包中物品的总价值: " + maxTotalValue);
            writer.write("\n\n已选物品列表:\n");

            for (Item item : selectedItems) {
                writer.write("重量: " + item.weight + ", 价值: " + item.value);
                writer.write("\n");
            }

            writer.close();
            System.out.println("输出成功！");
        } catch (IOException e) {
            e.printStackTrace();
        }
    }
}

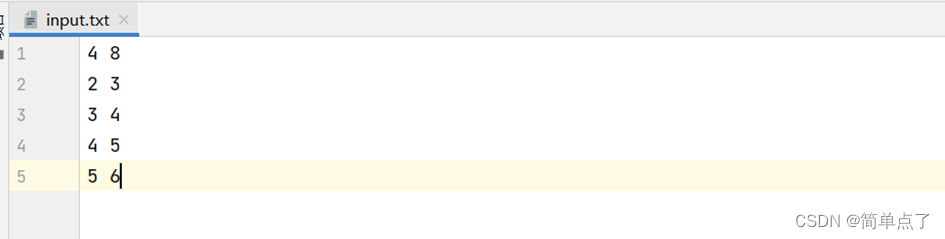
输入

 运行

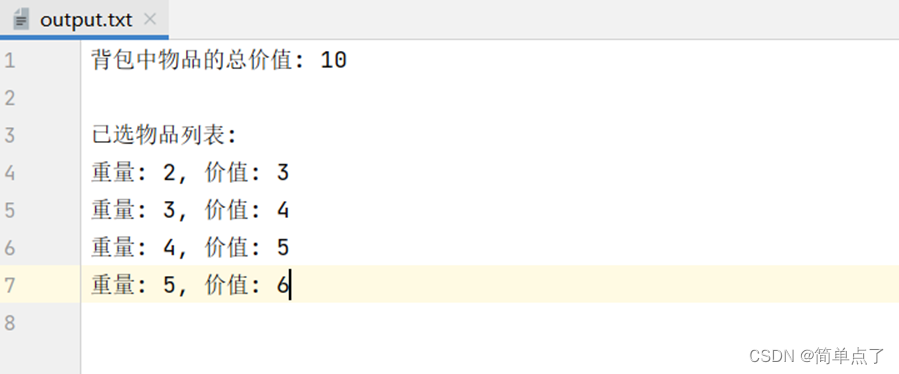
输出