Matlab求解基于RRT算法的自定义垛型的路径避障

news2024/11/27 11:49:20

目录

背景

1  RRT搜索算法

2  基于Matlab的RRT搜索算法

3  基于Matlab的自定义垛型绘制

4  基于RRT算法的自定义垛型的路径避障

背景

        在码垛机械臂路径规划过程中，需要根据现有箱子的码垛状态，给出下一个箱子的最佳码放无碰撞路径。RRT 快速搜索随机树算法是一种基于随机采样的增量式增长全局规划算法，也是在机械臂规划运动中最常使用的方法。

1  RRT搜索算法

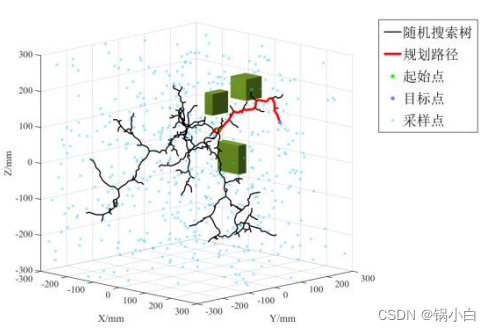
        在空间环境中已知机器人路径初始点 q_{init}和终止点q_{goal} ，RRT 算法以初始点 q_{init}作为根节点,在机器人的空间中产生随机点 q_{rand}，遍历随机树找到最近的叶子节点q_{near}，由节点 q_{near}向 q_{rand}的连线方向扩展 step 步长,得到新节点q_{new}并对其进行碰撞检测；若检测通过则将纳入随机树,否则放弃此次生长。 重复上述步骤,直到寻找到目标点为止,代表一次路径搜索完成,传统的 RRT 算法原理如下图 所示。

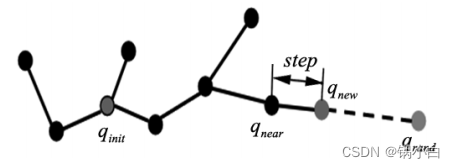
         RRT 算法与其他算法相比较更加适应于高维空间的规划,但是也有一些缺陷，由于随机点没有方向性，导致收敛速度较慢；在碰到的障碍物较多时，传统的 RRT 算法容易进入局部极小值的问题，针对传统RRT 算法的不足，目前常见的有目标偏置策略以加快收敛的改进算法。

        RRT的本质是基于空间采样的方法，虽然不是最优的，但是在概率上完备的。这类算法的核心在于随机采样，从父节点开始，随机在地图上生成子节点，连接父子节点并进行碰撞检测，若无碰撞，就扩展该子节点。

2  基于Matlab的RRT搜索算法

%% 确定障碍物空间(以长方体为例，在z方向上有共50的膨胀大小)
origin = [100,0,50];
rectsize=[200,30,150];

%下面开始绘制障碍物，[长 宽 高]=[200 30 100]的矩形
figure(1);
plotcube([200 30 100],[0  -15  -25],1,[1 0 0]);     % ([长 宽 高],[立方体初始顶点位置]，1，[颜色])
axis equal
%% 参数
source=[100 100 10];        % 初始点
goal=[100 -100 10];         % 目标点
stepsize = 5;
threshold = 5;
maxFailedAttempts = 10000;  % 最大搜索次数
display = true;
searchsize = [200 400 200];      %探索空间六面体
%% 绘制起点和终点
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");

tic;  % tic-toc: Functions for Elapsed Time
RRTree = double([source -1]);
failedAttempts = 0;
pathFound = false;

%% 循环（开始RRT搜索）
while failedAttempts <= maxFailedAttempts  % loop to grow RRTs
    %% chooses a random configuration
    if rand < 0.5
        sample = (rand(1,3)-[0 0.75 0.2]);   % random sample
        sample = sample .* searchsize;
    else
        sample = goal; % sample taken as goal to bias tree generation to goal
    end
    %% selects the node in the RRT tree that is closest to qrand
    [A, I] = min( distanceCost(RRTree(:,1:3),sample) ,[],1); % find the minimum value of each column
    closestNode = RRTree(I(1),1:3);
    %% moving from qnearest an incremental distance in the direction of qrand
    movingVec = [sample(1)-closestNode(1),sample(2)-closestNode(2),sample(3)-closestNode(3)];
    movingVec = movingVec/sqrt(sum(movingVec.^2));  %单位化
    if rand < 0.5
        newPoint=closestNode + stepsize * movingVec;
    else
        newPoint=goal;
    end
    % checkPath3判断路径与障碍物是否发生碰撞的函数
    if ~checkPath3(closestNode, newPoint, origin,rectsize) % if extension of closest node in tree to the new point is feasible
        failedAttempts = failedAttempts + 1;
        continue;
    end

    if distanceCost(newPoint,goal) < threshold, pathFound = true; break; end % goal reached
    [A, I2] = min( distanceCost(RRTree(:,1:3),newPoint) ,[],1); % check if new node is not already pre-existing in the tree
    if distanceCost(newPoint,RRTree(I2(1),1:3)) < threshold, failedAttempts = failedAttempts + 1; continue; end 
    
    RRTree = [RRTree; newPoint I(1)]; % add node
    failedAttempts = 0;
    if display, plot3([closestNode(1);newPoint(1)],[closestNode(2);newPoint(2)],[closestNode(3);newPoint(3)],'LineWidth',1); end
    pause(0.05);
end

if display && pathFound, plot3([closestNode(1);goal(1)],[closestNode(2);goal(2)],[closestNode(3);goal(3)]); end

% if display, disp('click/press any key'); waitforbuttonpress; end
if ~pathFound, error('no path found. maximum attempts reached'); end

%% retrieve path from parent information
path = goal;
prev = I(1);
while prev > 0
    path = [RRTree(prev,1:3); path];
    prev = RRTree(prev,4);
end

pathLength = 0;
for i=1:length(path(:,1))-1, pathLength = pathLength + distanceCost(path(i,1:3),path(i+1,1:3)); end % calculate path length
fprintf('processing time=%d \nPath Length=%d \n\n', toc, pathLength); 
figure(2)
plotcube([200 30 100],[0  -15  -25],1,[1 0 0]);
axis equal
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");
plot3(path(:,1),path(:,2),path(:,3),'LineWidth',2,'color','y');

         ①碰撞检测函数checkPath3.m为：

%% checkPath3.m	
function feasible=checkPath3(n,newPos,origin, size)
feasible=true;
size=size/2;
% disp(size);
movingVec = [newPos(1)-n(1),newPos(2)-n(2),newPos(3)-n(3)];
movingVec = movingVec/sqrt(sum(movingVec.^2)); %单位化
% 判断是否与障碍物立方体（以立方体中心为基准的空间边界计算）相交
if  (n(1) < (origin(1)+size(1)) && n(1) > (origin(1)-size(1))) && (n(2) < (origin(2)+size(2)) && n(2) > (origin(2)-size(2))) && (n(3) < (origin(3)+size(3)) && n(3) > (origin(3)-size(3)))
    feasible=false;
    return;
elseif  (newPos(1) < (origin(1)+size(1)) && newPos(1) > (origin(1)-size(1))) && (newPos(2) < (origin(2)+size(2)) && newPos(2) > (origin(2)-size(2))) && (newPos(3) < (origin(3)+size(3)) && newPos(3) > (origin(3)-size(3)))
    feasible=false;
    return;
else
    t=(origin(1)+size(1)-n(1))/movingVec(1);
    y=n(2)+movingVec(2)*t;
    z=n(3)+movingVec(3)*t;
    if (y < (origin(2)+size(2)) && y > (origin(2)-size(2))) && (z < (origin(3)+size(3)) && z > (origin(3)-size(3)))
        feasible=false;
        return;
    end
    t=(origin(1)-size(1)-n(1))/movingVec(1);
    y=n(2)+movingVec(2)*t;
    z=n(3)+movingVec(3)*t;
    if (y < (origin(2)+size(2)) && y > (origin(2)-size(2))) && (z < (origin(3)+size(3)) && z > (origin(3)-size(3)))
        feasible=false;
        return;
    end
    t=(origin(2)+size(2)-n(2))/movingVec(2);
    x=n(1)+movingVec(1)*t;
    z=n(3)+movingVec(3)*t;
    if (x < (origin(1)+size(1)) && x > (origin(1)-size(1))) && (z < (origin(3)+size(3)) && z > (origin(3)-size(3)))
        feasible=false;
        return;
    end
    t=(origin(2)-size(2)-n(2))/movingVec(2);
    x=n(1)+movingVec(1)*t;
    z=n(3)+movingVec(3)*t;
    if (x < (origin(1)+size(1)) && x > (origin(1)-size(1))) && (z < (origin(3)+size(3)) && z > (origin(3)-size(3)))
        feasible=false;
        return;
    end
    t=(origin(3)+size(3)-n(3))/movingVec(3);
    x=n(1)+movingVec(1)*t;
    y=n(2)+movingVec(2)*t;
    if (x < (origin(1)+size(1)) && x > (origin(1)-size(1))) && (y < (origin(2)+size(2)) && y > (origin(2)-size(2)))
        feasible=false;
        return;
    end
    t=(origin(3)-size(3)-n(3))/movingVec(3);
    x=n(1)+movingVec(1)*t;
    y=n(2)+movingVec(2)*t;
    if (x < (origin(1)+size(1)) && x > (origin(1)-size(1))) && (y < (origin(2)+size(2)) && y > (origin(2)-size(2)))
        feasible=false;
        return;
    end
end
end

        ②两点间距离计算函数distanceCost.m：

function h=distanceCost(a,b)         %% distanceCost.m
	h = sqrt(sum((a-b).^2, 2));
end

        运行的结果可得：

         可以看到，左侧为在空间中进行采样搜索的过程，当采样点与终点的连线不会与碰撞空间【膨胀后的rectsize=[200,30,150]】发生交叉碰撞后，直线到达终点的运动是最快的搜索结果。

3  基于Matlab的自定义垛型绘制

        这里设定堆垛均是长方体形状，借助plotcube函数，完成绘制。【plotcube】在使用时需要准备长方体的顶点位置、长宽高及颜色设置，故通过表格数据的读入【readmatrix("XXX.xls")】初始化长方体的参数设置。

        例.垛型长方体表格数据如下：

        注意： Matlab中只读取上述图片中的数值数据，即从第二行开始（第一行是BoxSize_L等字符串描述，数据处理的时候不读入）

         第一行的参数依次表示：

                BoxSize_L,BoxSize_W,BoxSize_H：堆垛箱子的长、宽、高

                Position_X,Position_Y,Position_Z：箱子的顶点位置坐标

                ColorMode：颜色设置的编号

                       参考Matlab官方文档中的RGB值的设置，颜色设置的代码如下：

ColorMode = [[0.4940 0.1840 0.5560];            
        [0.4660 0.6740 0.1880];
        [0.3010 0.7450 0.9330];
        [0.6350 0.0780 0.1840]];

                StackNum：同一堆箱子有一样的编号（这里设置的4堆箱子）

        基于上述表格的垛型数据的绘制代码如下：

Boxes = readmatrix('PalletBoxData_CSDN.xls','Range','C2:J18');    %'C2:J18'对应的是上述图片中的数值数据（第一行是BoxSize_L等字符串描述，数据处理的时候不读入）
ColorMode = [[0.4940 0.1840 0.5560];            % 指定绘图颜色
        [0.4660 0.6740 0.1880];
        [0.3010 0.7450 0.9330];
        [0.6350 0.0780 0.1840]];
figure(1);
plot_Obstacle(Boxes,ColorMode)         % 绘制堆垛现状（障碍物）



function plot_Obstacle(Boxes,ColorMode)
    
    % 绘制码垛
    % figure(1);
    hold on;
    for i=1:length(Boxes(:,1))
        plotcube([Boxes(i,1) Boxes(i,2) Boxes(i,3)],[Boxes(i,4) Boxes(i,5) Boxes(i,6)],1,ColorMode(Boxes(i,7),:));
        hold on
    end
    axis equal
end

        得到的结果图如下：

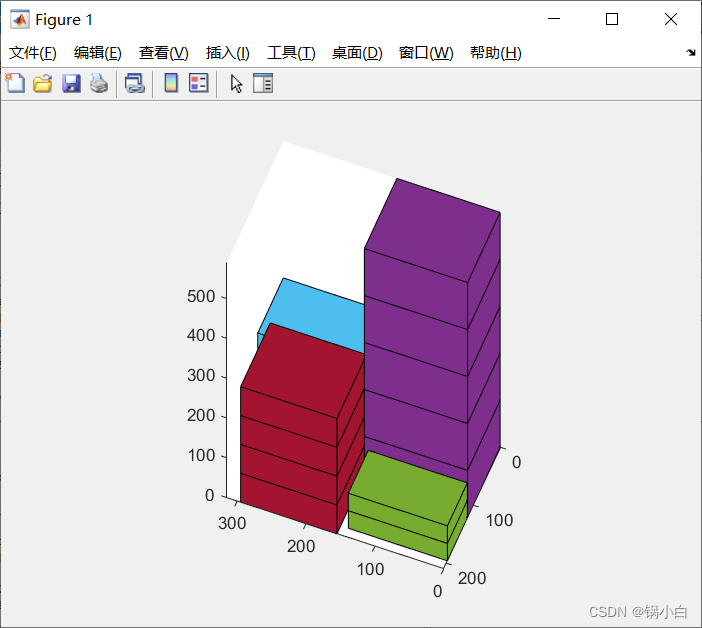
4  基于RRT算法的自定义垛型的路径避障

        即将2、3章的内容结合起来，先读入自定义的垛型表格数据，以此垛型为空间障碍物进行避障的RRT路径规划。【物理意义：机械臂在码垛过程中，携带箱子不能与已经存在的现有垛型发生碰撞。】

         整体代码如下：

clear all
clc

%% 读取码垛箱子的位置（上图中的表格数据）
Boxes = readmatrix('PalletBoxData_CSDN.xls','Range','C2:J18');
ColorMode = [[0.4940 0.1840 0.5560];            % 指定绘图颜色，参考https://ww2.mathworks.cn/help/matlab/creating_plots/specify-plot-colors.html
        [0.4660 0.6740 0.1880];
        [0.3010 0.7450 0.9330];
        [0.6350 0.0780 0.1840]];
figure(1);
plot_Obstacle(Boxes,ColorMode)         % 绘制堆垛现状（障碍物）

%% 初始化参数

% 障碍物空间
StackNum = Boxes(:,8);      % 获取码垛编号
StackHeight = [];   % 每一堆垛箱子的总高度
h_dialate = 0;     % 障碍物在高度上膨胀一定距离

[origin,rectsize] = calc_obstacleSpace(Boxes,StackNum,h_dialate,StackHeight);   % 计算障碍物空间
searchsize = [300,200,600];      %探索空间六面体

source=[315 -200 0];        % 初始点
goal=[0 200 88];         % 目标点
stepsize = 20;
threshold = 5;
maxFailedAttempts = 10000;  % 最大搜索次数
display = true;
searchsize = [200 400 200];      %探索空间六面体
%% 绘制起点和终点
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");

tic;  % tic-toc: Functions for Elapsed Time
RRTree = double([source -1]);
failedAttempts = 0;
pathFound = false;


%% 循环（开始RRT搜索）
while failedAttempts <= maxFailedAttempts  % loop to grow RRTs
    %% chooses a random configuration
    if rand < 0.5
        sample = (rand(1,3)-[0 0.75 0.2]);   % random sample
        sample = sample .* searchsize;
    else
        sample = goal; % sample taken as goal to bias tree generation to goal
    end
    %% selects the node in the RRT tree that is closest to qrand
    [A, I] = min( distanceCost(RRTree(:,1:3),sample) ,[],1); % find the minimum value of each column
    closestNode = RRTree(I(1),1:3);
    %% moving from qnearest an incremental distance in the direction of qrand
    movingVec = [sample(1)-closestNode(1),sample(2)-closestNode(2),sample(3)-closestNode(3)];
    movingVec = movingVec/sqrt(sum(movingVec.^2));  %单位化
    if rand < 0.5
        newPoint=closestNode + stepsize * movingVec;
    else
        newPoint=goal;
    end
    if ~checkPath3(closestNode, newPoint, origin,rectsize) % if extension of closest node in tree to the new point is feasible
        failedAttempts = failedAttempts + 1;
        continue;
    end

    t = [];
    for i = 1:4
       t(i) = ~checkPath3(closestNode, newPoint, origin(i,:),rectsize(i,:));
    end
            % 用  if判断及 或语句，保证不碰撞到每一个堆垛
    if t(1)||t(2)||t(3)||t(4)% if extension of closest node in tree to the new point is feasible
        failedAttempts = failedAttempts + 1;
        continue;                   % continue一旦被执行（if成立），就会终止当前循环，进行下一次循环。
    end

    if distanceCost(newPoint,goal) < threshold, pathFound = true; break; end % goal reached
    [A, I2] = min( distanceCost(RRTree(:,1:3),newPoint) ,[],1); % check if new node is not already pre-existing in the tree
    if distanceCost(newPoint,RRTree(I2(1),1:3)) < threshold, failedAttempts = failedAttempts + 1; continue; end 
    
    RRTree = [RRTree; newPoint I(1)]; % add node
    failedAttempts = 0;
    if display, plot3([closestNode(1);newPoint(1)],[closestNode(2);newPoint(2)],[closestNode(3);newPoint(3)],'LineWidth',1); end
    pause(0.05);
end

if display && pathFound, plot3([closestNode(1);goal(1)],[closestNode(2);goal(2)],[closestNode(3);goal(3)]); end

% if display, disp('click/press any key'); waitforbuttonpress; end
if ~pathFound, error('no path found. maximum attempts reached'); end



%% 最终轨迹展示
path = goal;
prev = I(1);
while prev > 0
    path = [RRTree(prev,1:3); path];
    prev = RRTree(prev,4);
end

pathLength = 0;
for i=1:length(path(:,1))-1, pathLength = pathLength + distanceCost(path(i,1:3),path(i+1,1:3)); end % calculate path length
fprintf('processing time=%d \nPath Length=%d \n\n', toc, pathLength); 
figure(2)
plot_Obstacle(Boxes,ColorMode)         % 绘制堆垛现状（障碍物）
axis equal
hold on;
scatter3(source(1),source(2),source(3),"filled","g");
scatter3(goal(1),goal(2),goal(3),"filled","b");
plot3(path(:,1),path(:,2),path(:,3),'LineWidth',2,'color','y');


%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%自定义函数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

% 绘制障碍物(以长方体为例，主要是方便计算)
function plot_Obstacle(Boxes,ColorMode)
    
    % 绘制码垛
    % figure(1);
    hold on;
    for i=1:length(Boxes(:,1))
        plotcube([Boxes(i,1) Boxes(i,2) Boxes(i,3)],[Boxes(i,4) Boxes(i,5) Boxes(i,6)],1,ColorMode(Boxes(i,7),:));
        hold on
    end
    axis equal
end
% 计算障碍物空间
% StackNum：堆垛的个数； h_dialate：堆垛障碍物的膨胀高度
% origin：膨胀后的障碍物空间的中心点； rectsize：膨胀后的障碍物空间
function [origin,rectsize] = calc_obstacleSpace(Boxes,StackNum,h_dialate,StackHeight)

    StackCount = hist(StackNum,unique(StackNum));       %获取每一堆有几个箱子
    origin = [];        % 膨胀后的障碍物空间的中心点
    rectsize=[];        % 膨胀后的障碍物空间
    for i=1:4          %%%%%%%%%%%%%%%%此时一共有4堆箱子
        h = Boxes(find(StackNum==i),3);         %分别求每一堆的箱子的高度（默认都是同一种箱子，高度相同）
        h_i = StackCount(i)*h(1);               %求每一堆的箱子总高度（目前累到的高度）
        StackHeight = [StackHeight,h_i];        %箱子总高度列到一个列表中
    
        x = Boxes(find(StackNum==i),4) + Boxes(find(StackNum==i),1)/2;         
        y = Boxes(find(StackNum==i),5) + Boxes(find(StackNum==i),2)/2;
        %分别求每一堆的箱子的中心点位置x,y,z坐标（默认都是同一种箱子，高度相同）
        x_center = x(1);
        y_center = y(1);
        z_center = h_i/2;
    
        obstacle_center = [x_center,y_center,z_center];
    
        %分别求每一堆的箱子的长、宽
        l = Boxes(find(StackNum==i),1);
        w = Boxes(find(StackNum==i),2);
        l_i = l(1);
        w_i = w(1);
    
        obstacle_volumn = [l_i,w_i,h_i+h_dialate];
    
        origin = cat(1,origin,obstacle_center);               % 膨胀后的障碍物空间的中心点
        rectsize = cat(1,rectsize,obstacle_volumn);
    end
end

        得到的运行结果为：

                ​​​​​​​

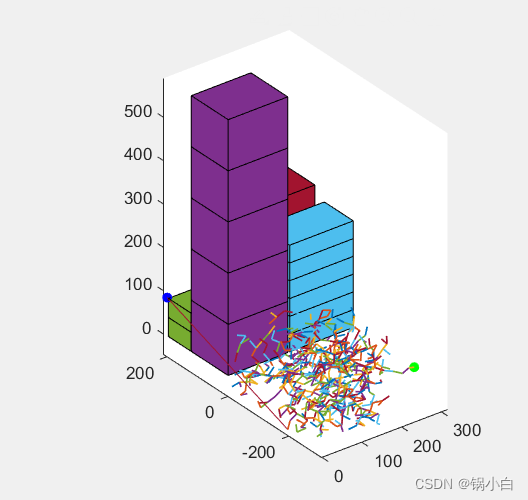
        多次实验发现，若步长（参数stepsize）较大，由于障碍物体积大且复杂，会导致搜索失败； 若步长较小，一直在空白搜索，不能收敛（在码垛旁边空白位置不断扩大搜索空间，没有效果）。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/780236.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

vue2项目 自定义详情组件

vue2项目 自定义详情组件

vue2项目 自定义详情组件 效果组件代码组件引入以及传参格式寄语 效果 组件代码 DetailFormRow.vue已经封装好&#xff0c;根据数据格式直接引用即可。 <template><div class"detail-form"><el-row class"detail-form-row" style"ma…
阅读更多...
基本函数、常见曲线图像

基本函数、常见曲线图像

基本函数图像是指一些常见的数学函数的图像&#xff0c;这些函数在数学和工程等领域中经常被使用。下面是一些常见的基本函数及其图像&#xff1a; 参考文献&#xff1a;同济版高等数学【第七版】上下册教材
阅读更多...
几张表格搞定Mysql的SQL语句

几张表格搞定Mysql的SQL语句

一、数据库的登录与退出 登录Mysqlmysql -uroot -p123退出Mysqlexit 二、对数据库的操作 查询所有数据库show databases;创建数据库create database 数据库名字;删除数据库drop database 数据库名字;查询创建数据库的具体语句show create database 数据库名字;使用数据库use…
阅读更多...
自学网络安全（黑客），遇到问题怎么解决

自学网络安全（黑客），遇到问题怎么解决

自学网络安全很容易学着学着就迷茫了&#xff0c;找到源头问题&#xff0c;解决它就可以了&#xff0c;所以首先咱们聊聊&#xff0c;学习网络安全方向通常会有哪些问题&#xff0c;看到后面有惊喜哦 1、打基础时间太长 学基础花费很长时间&#xff0c;光语言都有几门&#xf…
阅读更多...
RocketMQ的系统设计

RocketMQ的系统设计

消息存储 下图为producer、broker、consumer的交互过程 1.消息存储整体架构 CommitLog&#xff1a;消息主体以及元数据的存储主体&#xff0c;存储Producer端写入的消息主体内容(即Producer端投递的消息都会先写入CommitLog中)&#xff0c;消息内容不是定长的。单个文件大小默…
阅读更多...
代码随想录day8 | KMP 28.实现strStr() 459.重复的子字符串

代码随想录day8 | KMP 28.实现strStr() 459.重复的子字符串

文章目录 一、实现strStr()二、重复的子字符串 一、实现strStr() 先学学KMP算法&#xff0c;代码随想录 28.实现strStr() class Solution { public:void getNext(int* next, const string& s) {int j -1;next[0] j;for(int i 1; i < s.size(); i) { // 注意i从1开始…
阅读更多...
win 安装虚拟机 再安装macos

win 安装虚拟机 再安装macos

0 视频教程 windows虚拟机一键安装苹果系统macos&#xff0c;轻松拥有xcode环境_哔哩哔哩_bilibili在windows环境下vmware虚拟机一键安装macos Catalina10.15.7苹果系统&#xff0c;帮助学习ios编程的朋友们实现xcode环境。文字教程&#xff1a;https://www.dhzy.fun/archives…
阅读更多...
【Matlab】基于遗传算法优化 BP 神经网络的数据分类预测（Excel可直接替换数据）

【Matlab】基于遗传算法优化 BP 神经网络的数据分类预测（Excel可直接替换数据）

【Matlab】基于遗传算法优化 BP 神经网络的数据分类预测&#xff08;Excel可直接替换数据&#xff09; 1.模型原理2.文件结构3.Excel数据4.分块代码4.1 arithXover.m4.2 delta.m4.3 ga.m4.4 gabpEval.m4.5 initializega.m4.6 maxGenTerm.m4.7 nonUnifMutation.m4.8 normGeomSel…
阅读更多...
Qt ComboBox 下拉框设置多列

Qt ComboBox 下拉框设置多列

Qt ComboBox 下拉框设置多列 通过设置listview实现。 class MultiColumnComboBoxItemDelegate; class MultiColumnComboBoxListView;class MultiColumnComboBox : public QComboBox {Q_OBJECT public:explicit MultiColumnComboBox(QWidget *parent nullptr);~MultiColumnCo…
阅读更多...
Linux -- 进阶 自动挂载服务 ( autofs ) 介绍及安装 主配置文件分析

Linux -- 进阶 自动挂载服务 ( autofs ) 介绍及安装 主配置文件分析

背景引入 &#xff1a; 针对于 挂载 &#xff0c; 大家有没有思考过一个问题&#xff0c;如果我们需要挂载的文件或访问的远程数据甚至只是挂载一些设备&#xff0c;如果太多的话&#xff0c;数量很大的话&#xff0c;那 光每次挂载 敲的 mount 命令&#xff0c;都得敲很多遍…
阅读更多...
Flask 文件上传，删除上传的文件

Flask 文件上传，删除上传的文件

目录结构 app.py from flask import Flask, request, render_template, redirect, url_for import osapp Flask(__name__) BASE_DIR os.getcwd() UPLOAD_FOLDER os.path.join(BASE_DIR, testfile)app.route(/) def home():files os.listdir(UPLOAD_FOLDER)return render_t…
阅读更多...
如何对maven项目进行打jar包,出现不能打包的情况

如何对maven项目进行打jar包,出现不能打包的情况

若没有正确执行相应的操作,就会出现模块依赖无法找到的情况 Could not find artifact xxx:caro2o-system:pom:3.8.5 in public (https://maven.aliyun.com/repository/public)正确的打包操作 1.将现有的包清空 2.重新下载包 3.为确保数据正确,再次进行打包操作 4.观察控制…
阅读更多...
【Python】基于Python和Qt的海康威视相机开发

【Python】基于Python和Qt的海康威视相机开发

文章目录 0 前期教程1 前言2 例程解析3 图像获取4 其他问题与解决办法5 使用到的python包 0 前期教程 【项目实践】海康威视工业相机SDK开发小白版入门教程&#xff08;VS2015OpenCV4.5.1&#xff09; 1 前言 此前写了一篇基于C开发海康威视相机的博客&#xff0c;貌似看的人…
阅读更多...
设计模式结构型——享元模式

设计模式结构型——享元模式

目录 什么是享元模式 享元模式的实现 享元模式的特点 什么是享元模式 享元模式&#xff08;Flyweight Pattern&#xff09;是一种结构型设计模式&#xff0c;享元模式中的“享元”指被共享的单元&#xff0c;享元模式通过复用对象&#xff0c;以达到节省内存的目的。要求能够…
阅读更多...
[数学建模] [2019年A 模拟练习][层次分析法、熵值法、多目标优化、主成分分析法] 4. 深圳居民健康水平评估与测控模型研究

[数学建模] [2019年A 模拟练习][层次分析法、熵值法、多目标优化、主成分分析法] 4. 深圳居民健康水平评估与测控模型研究

1、前言 2019年“深圳杯”数学建模挑战赛A题 原题&#xff0c;这个是当时学校内部校赛所作&#xff0c;为了拿到参加国赛名额&#xff0c;也权当是做一个简单的练手。 本次练习属于综合评判类&#xff0c;常用的方法无非 层次分析法、熵值法、多目标优化、主成分分析法 等&am…
阅读更多...
简单了解内存泄漏（C++）

简单了解内存泄漏（C++）

文章目录 定义举例内存泄漏的危害内存泄漏的种类如何避免内存泄漏 定义 内存泄漏是指在程序运行过程中&#xff0c;申请的内存空间没有被正确释放或回收&#xff0c;导致这些内存无法再次使用的情况。简而言之&#xff0c;内存泄漏就是程序中已经分配的内存没有被及时释放&…
阅读更多...
APP抓包-代理转发绕过反代理+Xposed绕过证书校验

APP抓包-代理转发绕过反代理+Xposed绕过证书校验

某牛牛安卓app防抓包 夜神模拟器打开牛牛&#xff0c;出现网络连接失败等情况。明明网络一切正常&#xff0c;为什么会这样呢&#xff1f; 因为牛牛设置了反代理&#xff0c;而我开启了代理 burp也无任何牛牛的数据包产生 关闭代理之后牛牛就正常了&#xff0c;可恶的牛牛啊&am…
阅读更多...
Localizing Moments in Video with Natural Language论文笔记

Localizing Moments in Video with Natural Language论文笔记

0.文献地址 2017 Localizing Moments in Video with Natural Language 1.摘要 提出了Moment Context Network&#xff08;MCN&#xff09;有效地定位视频中的自然语言查询又提出了唯一识别对应时刻的文本描述的数据集DiDeMo 2.引言 作者提出了问题如果查询特定的时间段&am…
阅读更多...
算法竞赛备赛之经典数据结构训练提升，暑期集训营培训

算法竞赛备赛之经典数据结构训练提升，暑期集训营培训

1.链表与邻接表&#xff1a;树与图的存储 我们将结构体和指针结合来实现链表 struct Node {int val;Node * next; }; ​ new Node;//这样创建结点是相当慢的 我们算法主要是用数组来模拟链表&#xff0c;这样效率会高一些。 数组模拟单链表 邻接表&#xff1a;存储图和树 实…
阅读更多...
Spring Cloud【实现用户鉴权（什么是JWT、JWT原理、用户微服务、JWT工具类、用户服务实现JWT鉴权）】(八)

Spring Cloud【实现用户鉴权（什么是JWT、JWT原理、用户微服务、JWT工具类、用户服务实现JWT鉴权）】(八)

目录 Gateway解决如何允许跨域 服务网关Gateway实现用户鉴权_什么是JWT 服务网关Gateway实现用户鉴权_JWT原理 服务网关Gateway实现用户鉴权_用户微服务 服务网关Gateway实现用户鉴权_JWT工具类 服务网关Gateway实现用户鉴权_用户服务实现JWT鉴权 Gateway解决如何允许跨域…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023