一、实现strStr()

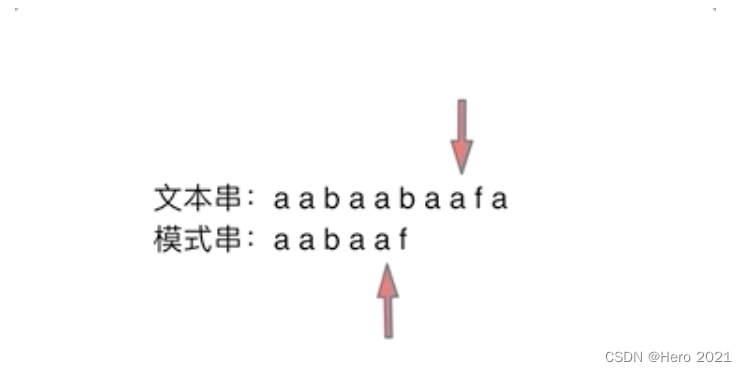
先学学KMP算法，代码随想录

28.实现strStr()

class Solution {
public:
    void getNext(int* next, const string& s) {
        int j = -1;
        next[0] = j;
        for(int i = 1; i < s.size(); i++) { // 注意i从1开始
            while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
                j = next[j]; // 向前回退
            }
            if (s[i] == s[j + 1]) { // 找到相同的前后缀
                j++;
            }
            next[i] = j; // 将j（前缀的长度）赋给next[i]
        }
    }
    int strStr(string haystack, string needle) {
        if (needle.size() == 0) {
            return 0;
        }
        int next[needle.size()];
        getNext(next, needle);
        int j = -1; // // 因为next数组里记录的起始位置为-1
        for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
            while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
                j = next[j]; // j 寻找之前匹配的位置
            }
            if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
                j++; // i的增加在for循环里
            }
            if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
                return (i - needle.size() + 1);
            }
        }
        return -1;
    }
};

二、重复的子字符串

459.重复的子字符串

暴力做法：

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        int n = s.length();
        for (int i = 1; i <= n / 2; i++) {
            if (n % i == 0) {
                string pattern = s.substr(0, i);
                int numRepeats = n / i;
                string constructedString = "";
                for (int j = 0; j < numRepeats; j++) {
                    constructedString += pattern;
                }
                if (constructedString == s) {
                    return true;
                }
            }
        }
        return false;
    }
};

该函数的思路是从字符串的长度的一半开始，依次尝试各个可能的子串长度。对于每一个可能的子串长度，我们构建一个重复多次的字符串，并与原始字符串进行比较。如果两个字符串相等，则说明可以通过子串重复多次构成，返回 true；否则继续尝试下一个可能的子串长度。如果循环结束后仍未找到符合条件的子串长度，则返回 false。

移动匹配：

class Solution {
public:
    bool repeatedSubstringPattern(string s) {
        string t = s + s;
        
        t.erase(t.begin()); 
        t.erase(t.end() - 1); // 掐头去尾
        
        if (t.find(s) != std::string::npos) return true;
        return false;
    }
};

KMP：

还没有完全理解KMP，先放会儿