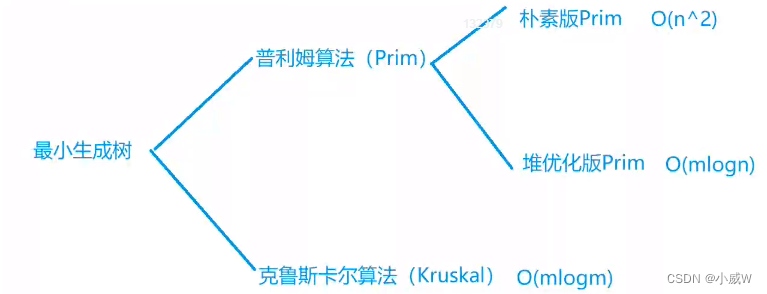
最小生成树介绍

最小生成树
有关树的定义

生成子图：生成子图是从原图中选取部分节点以及这些节点之间的边所组成的图。生成子图中的所有节点和边都必须在原图中存在。

生成树：一个连通无向图的生成子图，同时要求是树。也即在图的边集中选择 n - 1 条，将所有顶点连通。

我们定义无向连通图的 最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。

注意：只有连通图才有生成树，而对于非连通图，只存在生成森林。

朴素Prim算法

算法思路⭐

算法流程和 Dijkstra 算法非常相似。

Dijkstra 算法是用 t 更新其它点到起点的距离，而 Prim 用 t 更新其它点到 集合 的距离。

初始时各个点到集合的距离设置为 INF

循环 n 次，每次循环找到当前没在集合（集合就是最小生成树中节点的集合）且距离集合最近的节点。

将当前最近的节点 t 加入最小生成树中，然后使用 t 更新其它所有点(1~n)到集合之间的距离。

时间复杂度是：$O(n^2+m)$

例题：858. Prim算法求最小生成树

https://www.acwing.com/problem/content/description/860/

注意：图中可能存在重边和自环。
重边是指连接同一对顶点的多条边。在处理重边的时候，我们应当只保留权重最小的那条边，其他的边应当被忽略。
自环是指从一个顶点指向自身的边。在最小生成树中，自环是没有意义的，因为我们可以直接忽略这样的边。实际上，对于 Prim 算法，我们应当在初始化阶段，忽略这些自环，即将其赋予无穷大的权重。

另外注意图是无向图，因此在建图时应当同时更新$g[u][v]=g[v][u]=Math.min(g[u][v],w);$

import java.util.*;

public class Main {
    static final int INF = 0x3f3f3f3f;

    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), m = scanner.nextInt();
        // 边数很多，所以使用邻接矩阵来存储
        int[][] g = new int[n + 1][n + 1];
        for (int i = 1; i <= n; ++i) {
            Arrays.fill(g[i], INF);     // 对于自环也应该把距离设置成INF
        }
        for (int i = 0; i < m; ++i) {
            int u = scanner.nextInt(), v = scanner.nextInt(), w = scanner.nextInt();
            g[u][v] = g[v][u] = Math.min(g[u][v], w);   // 是无向图，所以g[u][v] = g[v][u]都要更新
        }

        // 求最小生成树的树边权重之和
        int sum = prim(g);
        System.out.println(sum > INF / 2? "impossible": sum);
    }

    static int prim(int[][] g) {
        int n = g.length - 1, res = 0;
        boolean[] st = new boolean[n + 1];      // 存储每个点是否已经在生成树中了
        int[] dis = new int[n + 1];             // 存储其它点到当前最小生成树的距离
        Arrays.fill(dis, 0x3f3f3f3f);       // 初始时距离都是 INF

        for (int i = 0; i < n; ++i) {
            // 找到当前和集合最近且不在集合中的节点t
            int t = -1;
            for (int j = 1; j <= n; ++j) {
                if (!st[j] && (t == -1 || dis[t] > dis[j])) t = j;
            }

            if (i != 0 && dis[t] == INF) return INF;    // 如果第一个节点没有把任何节点到最小生成树的距离变小

            // 将 t 加入最小生成树中去
            if (i != 0) res += dis[t];                  // 注意判断树中的第一个节点是不会贡献边权和的
            st[t] = true;

            // 使用 t 到各个节点的距离 更新 各个节点到当前最小生成树的距离
            for (int j = 1; j <= n; ++j) {
                dis[j] = Math.min(dis[j], g[t][j]);
            }
        }

        return res;
    }
}

Kruskal算法

算法思路⭐

1. 先将所有边按权重从小到大排序
2. 枚举每条边 a ，b ， w。如果 a， b 不连通就把这条边加入集合，即加入最小生成树。

如果使用 $O(m\log m)$ 的排序算法，并且使用 $O(m\alpha (m,n))$ 或 $O(m\log n)$ 的并查集，就可以得到时间复杂度为 $O(m\log m)$ 的 Kruskal 算法。

例题：859. Kruskal算法求最小生成树

https://www.acwing.com/activity/content/problem/content/925/

import java.util.*;

public class Main {
    static final int INF = 0x3f3f3f3f, N = 100005;
    static int[] p = new int[N];
    static int n;

    public static void main(String[] args){
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();
        int m = scanner.nextInt();

        // 记录所有的 m 个边
        int[][] edges = new int[m][3];
        for (int i = 0; i < m; ++i) {
            edges[i][0] = scanner.nextInt();
            edges[i][1] = scanner.nextInt();
            edges[i][2] = scanner.nextInt();
        }

        int res = kruskal(edges);
        System.out.println(res == INF? "impossible": res);
    }

    static int find(int x) {
        if (x != p[x]) p[x] = find(p[x]);
        return p[x];
    }

    static int kruskal(int[][] edges) {
        // 按照权重升序排序
        Arrays.sort(edges, (a, b) -> a[2] - b[2]);
        Arrays.setAll(p, e -> e);       // 初始化并查集

        int res = 0, cnt = 0;
        for (int[] edge: edges) {
            int x = edge[0], y = edge[1];
            if (find(x) != find(y)) {
                p[find(x)] = find(y);
                res += edge[2];
                cnt++;
            }
        }

        if (cnt < n - 1) return INF;
        return res;
    }
}