RNN学习笔记
时间序列
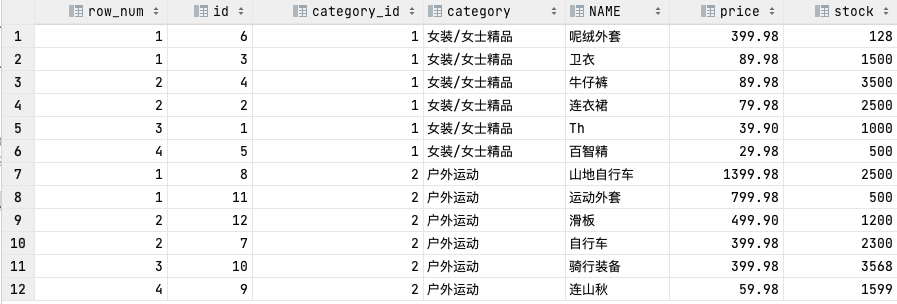
将单词序列转换为向量,这里有五个单词,然后对于每一个单词都进行独热编码,编码成一个特定的向量。

对于RNN网络,需要一次性读取多个句子,那么涉及到batch_size,这里第二个表达就是:batch,单词,单词的表达方式

RNN原理
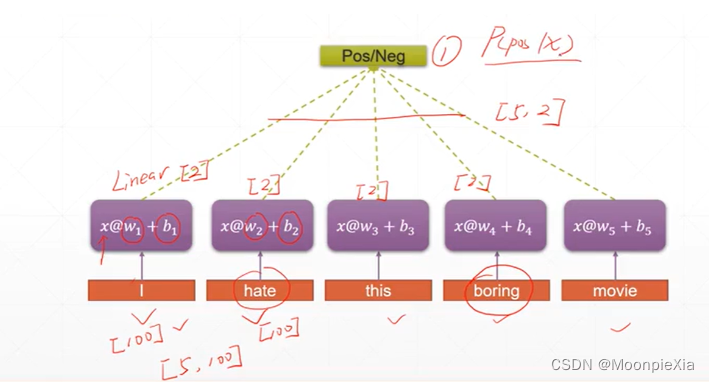
这里生成一个5 x 100的向量,对于每一个单词我们都使用100个特征进行表示,然后经过每一个线性层,这100维的向量转换为更小的向量 比如五个向量特征,那么对于一个句子的每一个单词都进行这样的提取特征,那么就需要对每一个单词都进行线性层的变换,最后得到一个5x5的向量
但是上面的做法有两个缺点:
- 单词数量太多 句子太长
- 参数两太多 对于每一个单词都需要生成特定的w b的线性层 这样参数过多
- 只考虑每一个单词 没有考虑语境信息
那么,对于每一个线性层,我们不仅输入每一个单词的向量,还需要输入语境信息h
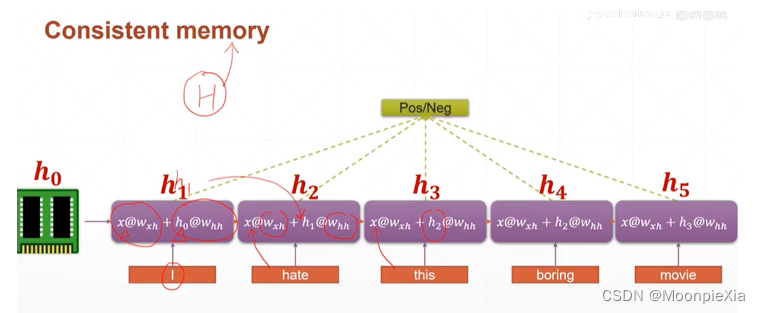
现在举一个例子,对于每一个单词我们使用 100个特征进行表示,对于一个句子五个单词就是5 x 100的向量表示,那么我们选择batch_size是3 一次输入三个单词,那么对于每次的输入xt,就是[3,100]的向量,我们初始化语境信息向量h[0,0…],输入网络
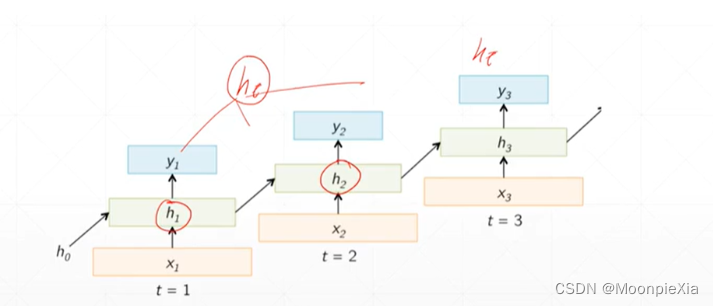
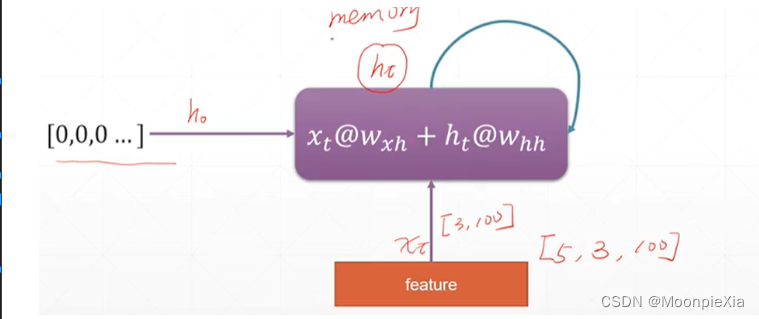
针对上面的讲述,整理成公式化,对于每一个输出ht 都是由ht-1 和xt得到的,也就是当前层的输入xt和上一层计算的输出作为当前层的输入,然后,使用Whh和WXh分别对输入的xt和ht-1进行特征提取,得到的输出向量经过激活函数进行激活
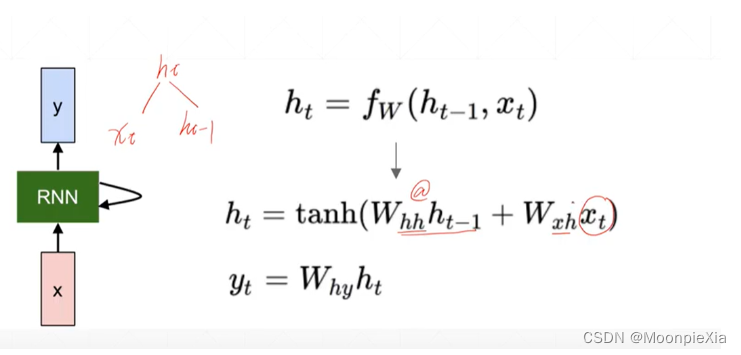
如何推导出梯度?
为RNN网络的权重whh和Wxh都是共享的,那么最后的输出一定是关系到每一个时刻的权重,所以我们需要使用损失对每一个时刻的权重进行求导,然后进行累加
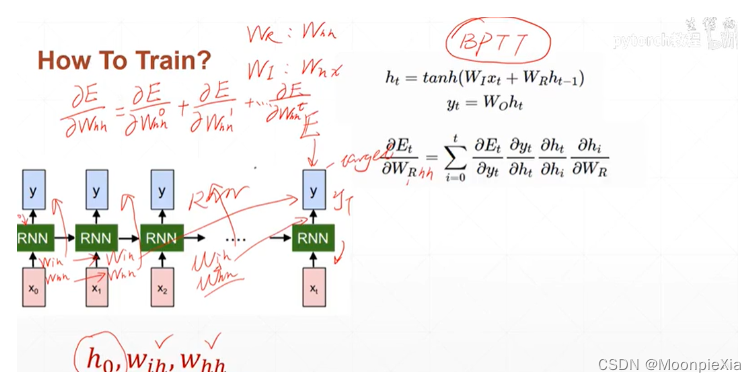
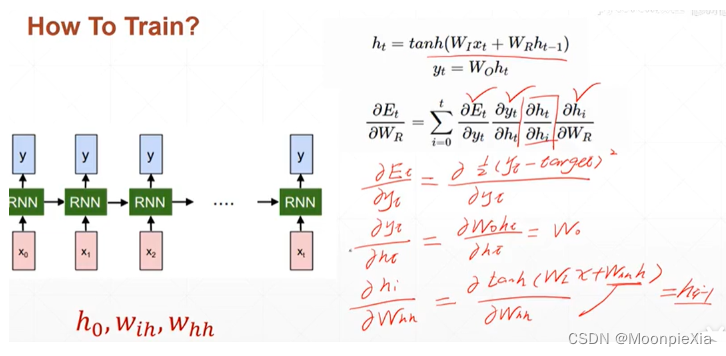
对于ht求导hi
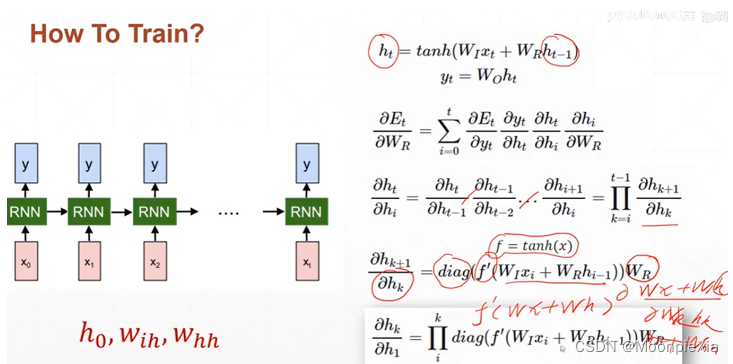
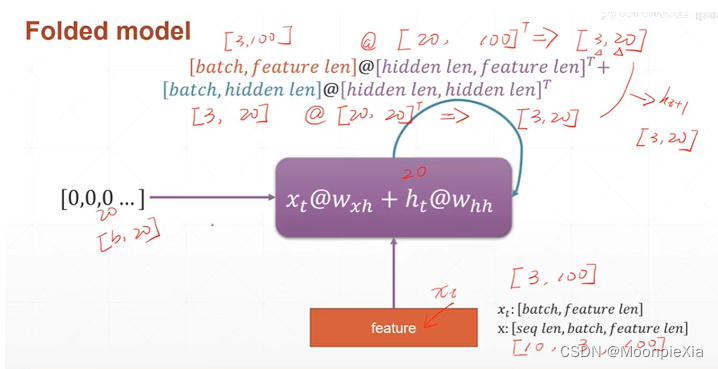
RNN Layer的使用
输入的向量xt是[3,100],那么 Wxh是[100,20]的形状的参数向量,也就是说相乘之后变成了[3,20] 原先单词使用100个特征进行表示,现在使用20个特征进行表示。同样的对于语境信息向量ht[3,20] 那么Whh是[20,20]的向量,想成之后变成了[3,20],然后两个[3,20]的向量相加得到ht+1向量
rnn=nn.RNN(100,10) #每个单词用100维表示,memory/hidden为10维
rnn._parameters.keys()
#out:odict_keys(['weight_ih_l0', 'weight_hh_l0', 'bias_ih_l0', 'bias_hh_l0'])
rnn.weight_hh_l0.shape,rnn.weight_ih_l0.shape
#out:(torch.Size([10, 10]), torch.Size([10, 100]))
rnn.bias_hh_l0.shape,rnn.bias_ih_l0.shape
out:(torch.Size([10]), torch.Size([10]))
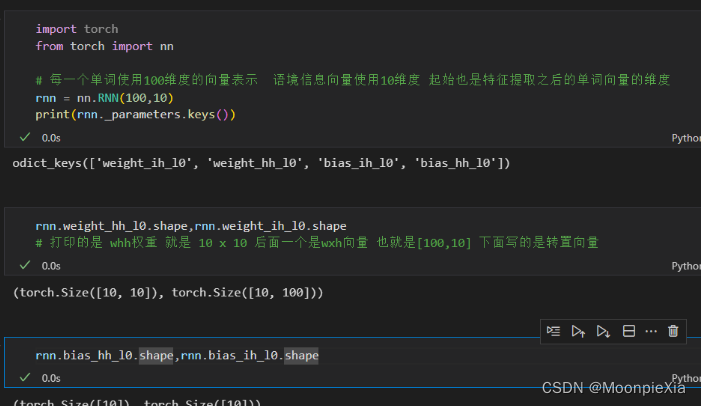
这里创建了一个RNN模型,其中参数100表示输入数据的特征维度,每个单词用100维的向量表示;参数10表示RNN内部隐层的大小,也称为记忆维度,即隐状态的维度。
nn.RNN模块有四个可训练参数,它们是:
weight_ih_l0: 输入到隐层的权重矩阵,形状为(10, 100),表示从输入层到隐层的权重参数。
weight_hh_l0: 隐层到隐层的权重矩阵,形状为(10, 10),表示从上一时刻隐层到当前时刻隐层的权重参数。
bias_ih_l0: 输入到隐层的偏置向量,形状为(10),表示从输入层到隐层的偏置参数。
bias_hh_l0: 隐层到隐层的偏置向量,形状为(10),表示从上一时刻隐层到当前时刻隐层的偏置参数。
输入到隐层的权重矩阵(weight_ih_l0)的形状为 (hidden_size, input_size),而不是 (input_size, hidden_size)。这里 (10, 100) 表示有 10 个隐状态单元(记忆单元)和每个单词用 100 维的向量表示作为输入特征。
单层的RNN
因为是单层的RNN,那么h向量只有一个
# RNN创建
rnn = nn.RNN(input_size = 100,hidden_size = 20,num_layers=1)
print(rnn)
# 10代表每一个句子的单词数量 3代表三个句子 100 代表每一个单词的维度
x = torch.randn(10,3,100)
# 第一个参数是输入向量x 第二个参数是h向量 只有一个单词 每一层三个句子 每一个单词使用20个维度
out,h = rnn(x,torch.zeros(1,3,20))
# 最后的输出out 是一个 10 x 3 x 20 的向量 也就是被提取成20个维度 然后h是一个1 3 20的向量
print(out.shape,h.shape)
多层的RNN
因为有多层RNN,那么就有多个h向量,但是out输出形状不会变
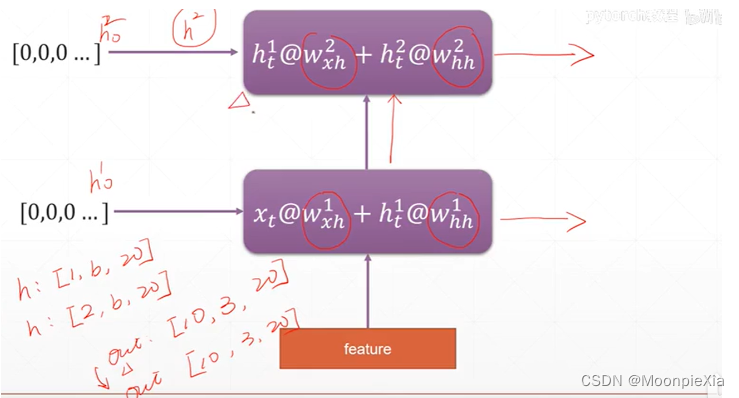
rnn = nn.RNN(input_size = 100,hidden_size = 20,num_layers = 4)
print(rnn)
x = torch.randn(10,3,100)
# 这里面的h 是多层的 应该是[4,3,20]
out,h = rnn(x)
print(out.shape,h.shape)
单层RNNCell
处理三个句子,每一个句子10个单词,每一个单词使用长度100的向量,送入RNN的shape就是[10,3,100]
如果使用RNNCell 针对每一个时刻都分开处理,这里十个单词就是十个时刻,每次输入的向量是[3,100] 那么计算单元运行十次,
显然,RNNCelll没办法想RNN直接求出网络的输出,那么只需要将最后一层每一个时刻得输出h组合起来。out = torch.stack([h1,h2,…,ht])
# 100代表输入得特征维度 20代表提取的特征维度
cell = nn.RNNCell(100,20)
# 初始化输入 某一个时刻得输入
x = torch.randn(3,100)
# 初始化所有时刻得输入
xs = [torch.randn(3,100) for i in range(10)]
# 初始化隐藏层记忆单元
h = torch.zeros(3,20)
# 针对每一个时刻得输入 传入RNN单元
for xt in xs:
h = cell(xt,h)
# 查看最后的输出
print(h.shape)
多层RNNCell
# 定义两层计算单元
cell_l0 = nn.RNNCell(100,30)
cell_l1 = nn.RNNCell(30,20)
# 定义两层的隐藏单元
h_l0 = torch.zeros(3,30)
h_l1 = torch.zeros(3,20)
# 初始化原始输入
xs = [torch.randn(3,100) for i in range(4)]
for xt in xs:
h_l0 = cell_l0(xt,h_l0)
h_l1 = cell_l1(h_l0,h_l1)
print(h_l0.shape)
print(h_l1.shape)
简单案例
预测正弦曲线的下一段波形
因为是输入一段波形曲线,不同于一个句子,句子中的每一个单词都是不能直接输入,需要做embedding,也就是对每一个单词进行编码成一个向量,但是波形曲线每一个点都是一个数字,不需要做embedding,那么如果给出五十个点,只提供一条曲线,那么seq_len = 50,feature_len =1,那么输入就是[50,1,1],但是batch需要提前,也就是输入[1,50,1],但是因为最后的输出是[seq_len,batch,hidden_len] 我们还是需要添加一个线性层变换一下,不能是hidden_len,需要变换成1 也就是[seq_len,batch,1]
- 定义网络
class Net(nn.Module):
def __init__(self):
super(Net,self).__init__()
# RNN
self.rnn = nn.RNN(
input_size = 1, # feature_len = 1
hidden_size = 16, # 隐藏层记忆单元尺寸
num_layers = 1,# 层数
batch_first = True # 确保输入时 按照[batch,seq_len,feature_len]的模式 1 x 50 x 1
)
# 对RNN 进行参数初始化
for p in self.rnn.parameters():
nn.init.normal_(p,mean=0.0,std=0.001)
# 输出层 直接使用一个线性变换 吧每一个时刻的记忆单元的Hidden_len的输出为所需要的feature_len = 1 因为是一个数据点
# 50 x 16 -> 50 x 1
self.linear = nn.Linear(16,1)
def forward(self,x,h):
# 这里的out原始形状是 1 x 50 x 16 最后变成 50 x 16
# h的原始形状是 1x 1 x 16
out,h = self.rnn(x,h)
# 因为最后需要传递给线性层处理,所以需要展平
out = out.view(-1,16)
out = self.linear(out)
# 在把batch维度添加进去
out = out.unsqueeze(dim=0)
return out,h
- 训练网络
lr = 0.01
model = Net()
from torch import nn, optim
criterion = nn.MSELoss() # 均方差损失函数
optimizer = optim.Adam(model.parameters(),lr) # 学习率
# 初始化记忆单元
h = torch.zeros(1,1,16)
# 生成样本数据
num_points = 50
seq_len = num_points - 1
import numpy as np
for iter in range(6000):
k = np.random.randint(3, size=1)[0]
# 取点的区间是[k, k+10],均匀地取num_points个点
time_steps = np.linspace(k, k + 10, num_points)
# 在这num_points个时刻上生成函数值数据
data = np.sin(time_steps)
# 将数据从shape=(num_points,)转换为shape=(num_points,1)
data = data.reshape(num_points, 1) # feature_len=1
# 输入前49个点(seq_len=49),即下标0~48
x = torch.tensor(data[:-1]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 预测后49个点,即下标1~49
y = torch.tensor(data[1:]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 至此,生成了x->y的样本对, x和y都是shape如上面所写的序列
# 将数据输入
out,h = model(x,h)
# h在循环中被
h = h.detach()
# 计算和预期输出之间的损失
loss = criterion(out,y)
# 更新网络参数
model.zero_grad()
# 计算梯度
loss.backward()
# 优化
optimizer.step()
if iter % 1000 == 0:
print("迭代次数:{}, loss:{}".format(iter + 1, loss.item()))
- 测试
from matplotlib import pyplot as plt
# 先用同样的方式生成一组数据x,y
k = np.random.randint(3, size=1)[0]
time_steps = np.linspace(k, k + 10, num_points)
data = np.sin(time_steps)
data = data.reshape(num_points, 1) # feature_len=1
x = torch.tensor(data[:-1]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
y = torch.tensor(data[1:]).float().view(1, seq_len, 1) # batch,seq_len,feature_len
# 用于记录预测出的点
predictions = []
# 取训练时输入的第一个点,即在x(1,seq_len,1)取seq_len里面第0号的数据
# 这里将输入seq_len'设置为1(而不是49)
# 输入什么长度的数据会自动调整网络结构来给出输出
input = x[:, 0, :]
# 输入的shape变成标准的(batch=1,seq_len'=1,feature_len=1)
input = input.view(1, 1, 1)
# 迭代seq_len次,每次预测出一个点
for _ in range(x.shape[1]):
# 送入模型得到预测的序列,输入了一个点的序列也就输出了(下)一个点的序列
pred, h = model(input, h)
# 这里将预测出的(下一个点的)序列pred当成输入,来给到下一次循环
input = pred
# 把里面那个点的数取出来记录到列表里
# 这里用ravel()而不用flatten(),因为后者是原地操作,会改变pred也就是input
predictions.append(pred.detach().data.numpy().ravel()[0])
# 绘制预测结果predictions和真实结果y的比较
plt.scatter(time_steps[1:], y.data.numpy().ravel())
plt.scatter(time_steps[1:], predictions, c='r')
plt.show()