个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【数据结构初阶（C实现）】

我们直到一般的排序都是通过关键字的比较和移动这两种操作来进行排序的。
而今天介绍的基数排序并不是依靠关键字的比较和移动来进行数据元素的排序。
基数排序是一种借助多关键字的思想对单逻辑关键字进行排序方法。

1️⃣样例演示

基数排序的概念描述和思想比较难懂，所以我们先来一个样例演示。然后再来细细品味基数排序的概念和思想。

我们对下面这个数组中的元素进行排序来进行演示：

int arr[10] = { 177 208 64 910 586 182 405 239 83 1 }

我们按照最低位优先法发来进行排序，可以看到数组中最高位为百位，所以总共要进行三轮排序。

第一趟：

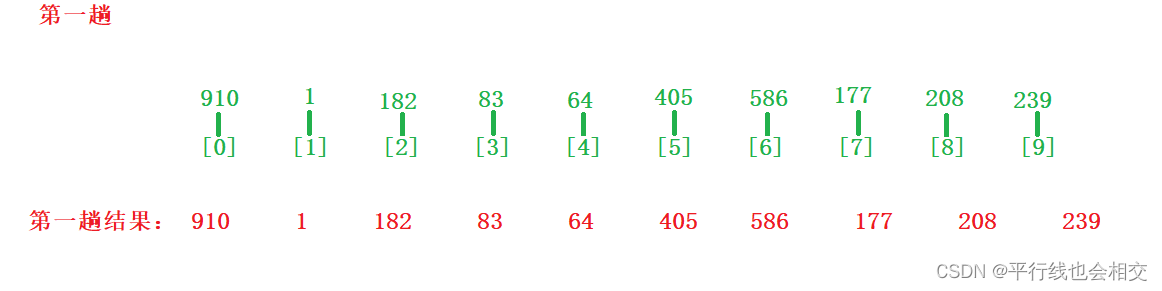
第二趟：

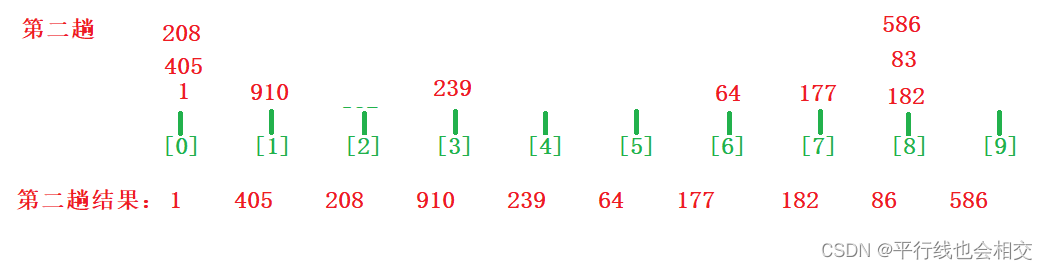
第三趟：

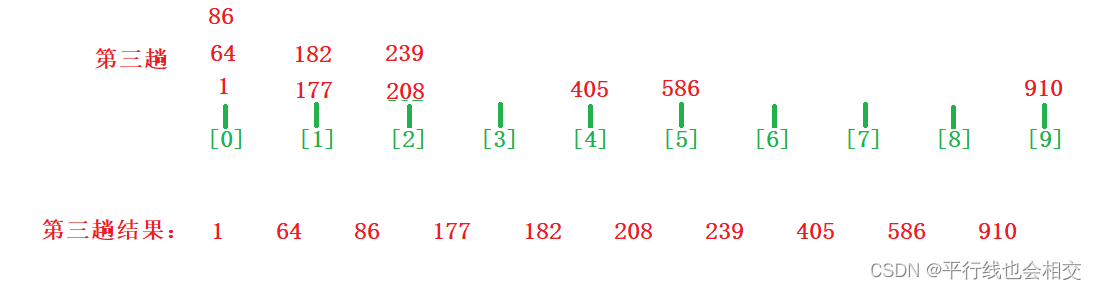
可以看到每趟排序后回收数据时按照队列先进先出的思想来进行回收数据。

2️⃣基数排序介绍

基数排序（Radix Sort）是一种非比较排序算法，它将待排序的元素按照位数从低位到高位（从高位到低位也可以）依次进行排序。（本文按照从低位到高位为例进行演示）。

3️⃣算法思想

基数排序的算法思想可以概括为以下几个步骤：

1.确定待排序元素的最高位数（即最大位数）：首先需要确定待排序元素中的最大值，并计算出它的位数，这决定了排序过程需要进行多少轮。
2.按照最低有效位进行一次稳定的排序：从最低位开始，将待排序元素按照最低有效位的值进行稳定排序，可以使用计数排序或桶排序等算法实现。排序后，元素相对于最低位来说是有序的。
3.按照次低有效位进行稳定排序：将上一轮排序得到的有序序列按照次低有效位的值进行稳定排序。这样，在当前位和低位均已有序的前提下，排序后整个序列相对于当前位来说是有序的。
4.重复执行步骤3，直到按照最高位进行排序：依次对每一位进行稳定排序，直到按照最高位排序完成。最终得到的序列即为完全有序的结果。

4️⃣代码示例

#include<iostream>
#include<queue>
using namespace std;

#define RADIX 10
#define K 3          //排序3轮

queue<int> Q[RADIX];

int getkey(int value, int k)
{
	int key = 0;
	while (k >= 0)
	{
		key = value % 10;
		value /= 10;
		k--;
	}
	return key;
}

void distribute(int arr[], int left, int right,int k)
{
	for (int i = left; i < right; i++)
	{
		int key = getkey(arr[i], k);
		Q[key].push(arr[i]);
	}
}

void collect(int arr[])
{
	int k = 0;
	for (int i = 0; i < RADIX; i++)
	{
		while (!Q[i].empty())
		{
			arr[k++] = Q[i].front();
			Q[i].pop();
		}
	}
}
void ridixsort(int arr[], int left, int right)
{
	for (int i = 0; i < K; i++)
	{
		//分发数据
		distribute(arr, left, right, i);


		//回收数据
		collect(arr);
	}
	
}

int main()
{
	int arr[] = { 177 ,208 ,64, 910 ,586, 182, 405, 239, 83, 1 };
	int n = sizeof(arr) / sizeof(arr[0]);
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");

	ridixsort(arr, 0, n);

	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	printf("\n");

	return 0;
}

运行结果如下：

5️⃣总结

关于基数排序的几大要点总结一下：

1.基数排序是一种非比较排序算法，通过将待排序的元素按照位数进行拆分，并依次对每一位进行稳定的排序，从而达到整体有序的效果。
2.基数排序的稳定性非常重要，即在每一轮排序时，保证相同位上值相等的元素的相对顺序不变。
3.确定待排序元素的最高位数，这决定了排序过程需要进行多少轮。
4.对每一位依次进行稳定排序，可以使用计数排序、桶排序等方法来实现。
5.基数排序的时间复杂度为O(dn)，其中d为待排序元素的最大位数，n为元素的个数。空间复杂度为O(n + k)，其中k为计数排序或桶排序中桶的个数。
6.基数排序适用于待排序元素位数相对较小且范围较小的情况，但如果待排序元素的位数差异较大，或者位数较多时，性能可能受到影响。
7.基数排序是稳定的排序算法，可以应用于对整数、字符串等类型的数据进行排序。