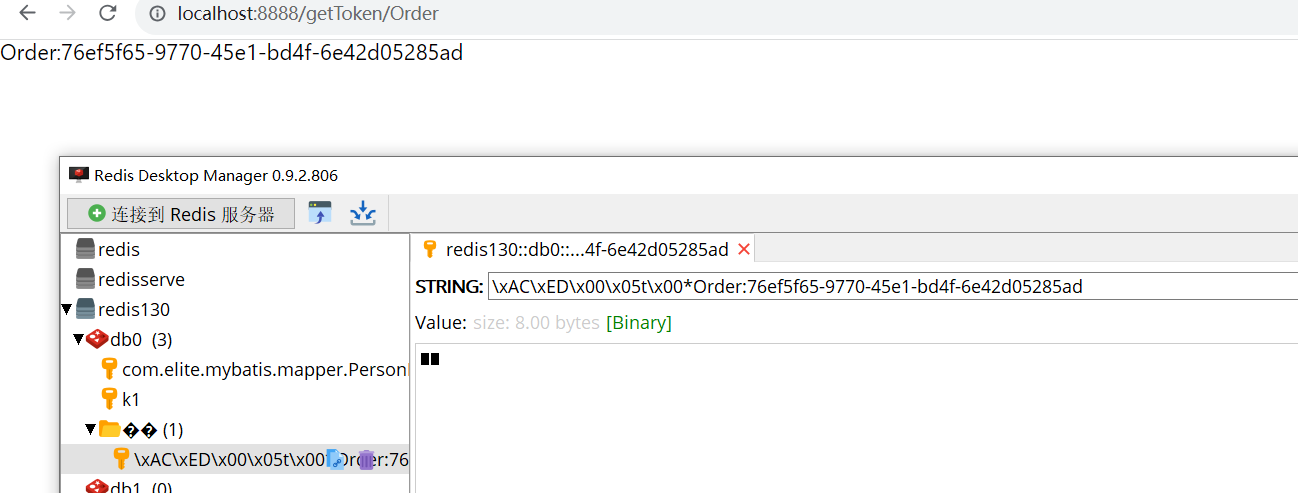
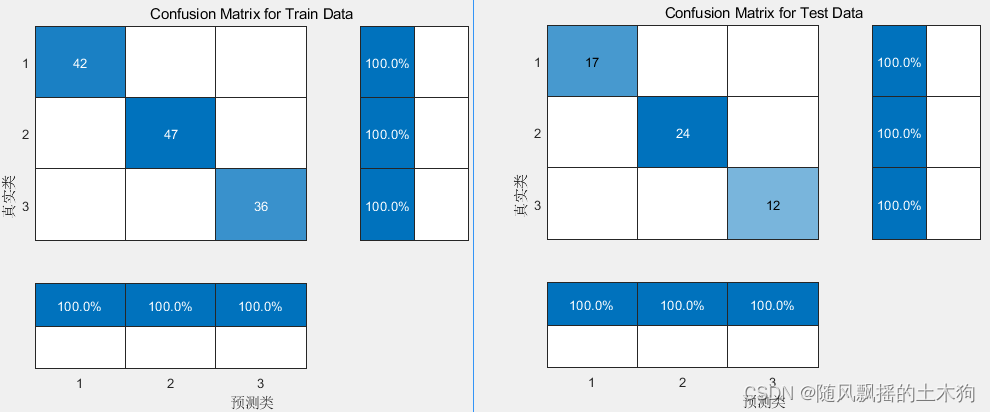
2023.7.22

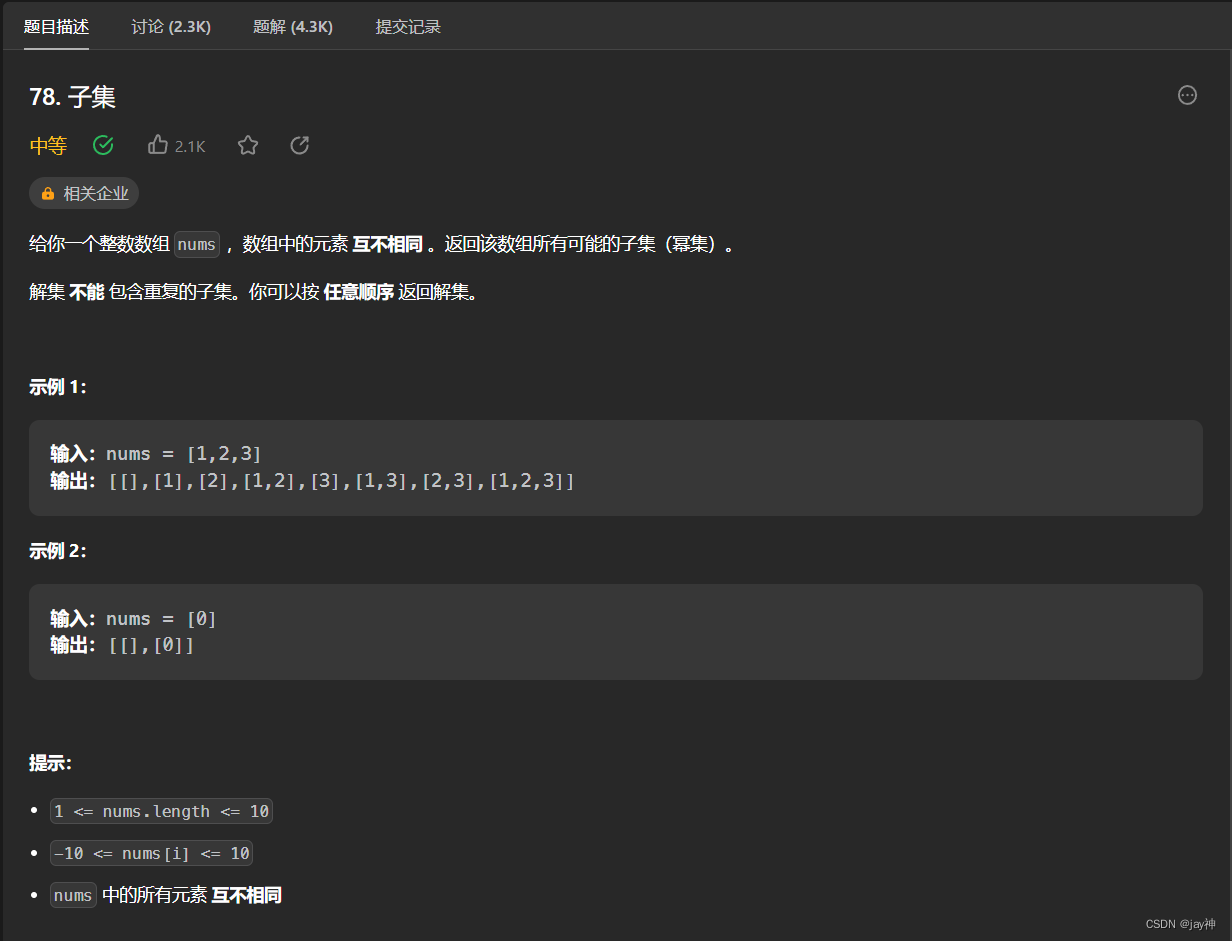
        本题为回溯系列的一道标准模板题。 如果将回溯问题抽象为一棵树的话，那么之前的组合、分割问题都是为了找到这棵树的叶子节点，而子集是要找到这棵树的所有节点。

        然后要注意，子集是无序的，即{1，2}和{2，1}是相同的，所以回溯的for循环中，i需要从start开始而不是从0开始。

        接下来上代码：

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;

    void backtrating(vector<int> nums,int start)
    {
        ans.push_back(path);
        //此中止条件可以不要，因为当start超出nums数组，意味着for循环也结束了。
        // if(start > nums.size()-1)
        // {
        //     return;
        // }
        for(int i=start; i<nums.size(); i++)
        {
            path.push_back(nums[i]);
            backtrating(nums,i+1);
            path.pop_back();
        }
    }

    vector<vector<int>> subsets(vector<int>& nums) {
        backtrating(nums,0);
        return ans;
    }
};

        时间复杂度分析：由于每个元素都有选取和不选取两种状态，一共有n个元素的话，就有2^n种子集。 又因为每个子集都需要加入数组，所以总时间复杂度为O(n × 2^n)。

        空间复杂度：O(n)。