👀樊梓慕:个人主页
🎥个人专栏:《C语言》《数据结构》《蓝桥杯试题》
🌝每一个不曾起舞的日子,都是对生命的辜负。
目录
前言:
一、隐式类型转换
(一)整型提升的意义
(二)如何进行整型提升呢?
二、算数转换
三、操作符的属性
(一)操作符优先级汇总
(二)一些问题表达式
前言:
本篇文章汇总了在进行表达式求值时一些容易出现错误的点,介绍整型提升的相关内容,并提供操作符优先级汇总表格供大家参考,希望大家多多支持博主创作,博主会持续带来更多优质内容🌍
=========================================================================
GITEE相关代码:🌟fanfei_c的仓库🌟
=========================================================================
一、隐式类型转换
假如有这样一段代码:
char a, b, c;
...
a = b + c;计算机是以什么逻辑来进行计算的呢?
实际上,C的整型算术运算总是至少以缺省(默认)整型类型的精度来进行的。
为了获得这个精度,表达式中的字符(char)和短整型操作数(short)在使用之前被转换为普通整型(int),这种转换称为整型提升。
(一)整型提升的意义
- 表达式的整型运算要在CPU的相应运算器件内执行,CPU内整型运算器(ALU)的操作数的字节长度,一般就是int的字节长度,同时也是CPU的通用寄存器的长度。
- 因此,即使两个char类型的相加,在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
- 通用CPU(general-purpose CPU)是难以直接实现两个8比特字节直接相加运算(虽然机器指令中可能有这种字节相加指令)。所以,表达式中各种长度可能小于int长度的整型值,都必须先转换为int或unsigned int,然后才能送入CPU去执行运算。
所以上面的代码逻辑为:b和c的值被提升为普通整型,然后再执行加法运算。
加法运算完成之后,结果将被截断,然后再存储于a中。
(二)如何进行整型提升呢?
整形提升是按照变量的数据类型的符号位来提升的。
- 负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位:
1111111
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为1
提升之后的结果是:
11111111111111111111111111111111
- 正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位:
00000001
因为 char 为有符号的 char
所以整形提升的时候,高位补充符号位,即为0
提升之后的结果是:
00000000000000000000000000000001
- 无符号整形提升,高位补0
举个栗子🌰:
//实例1
int main()
{
char a = 0xb6;
short b = 0xb600;
int c = 0xb6000000;
if (a == 0xb6)
printf("a");
if (b == 0xb600)
printf("b");
if (c == 0xb6000000)
printf("c");
return 0;
}答案:c
分析:实例1中的a,b要进行整形提升,但是c不需要整形提升。
a,b整形提升之后,变成了负数,所以表达式 a==0xb6,b==0xb600 的结果是假,但是c不发生整形提升,则表达式 c==0xb6000000 的结果是真。
//实例2
int main()
{
char c = 1;
printf("%u\n", sizeof(c));
printf("%u\n", sizeof(+c));
printf("%u\n", sizeof(-c));
return 0;
}答案:1 4 4
分析:实例2中的c只要参与表达式运算,就会发生整形提升,表达式 +c ,就会发生提升,所以 sizeof(+c) 是4个字节。表达式 -c 也会发生整形提升,所以 sizeof(-c) 是4个字节,但是 sizeof(c) ,就是1个字节。
二、算数转换
那么如果表达式的各个操作数属于不同的类型时,又该如何处理呢?
此时就需要将其中一个操作数转换为另一个操作数的类型,否则就无法计算,下面给出操作数类型转换的优先级,该层次体系成为寻常算数转换。
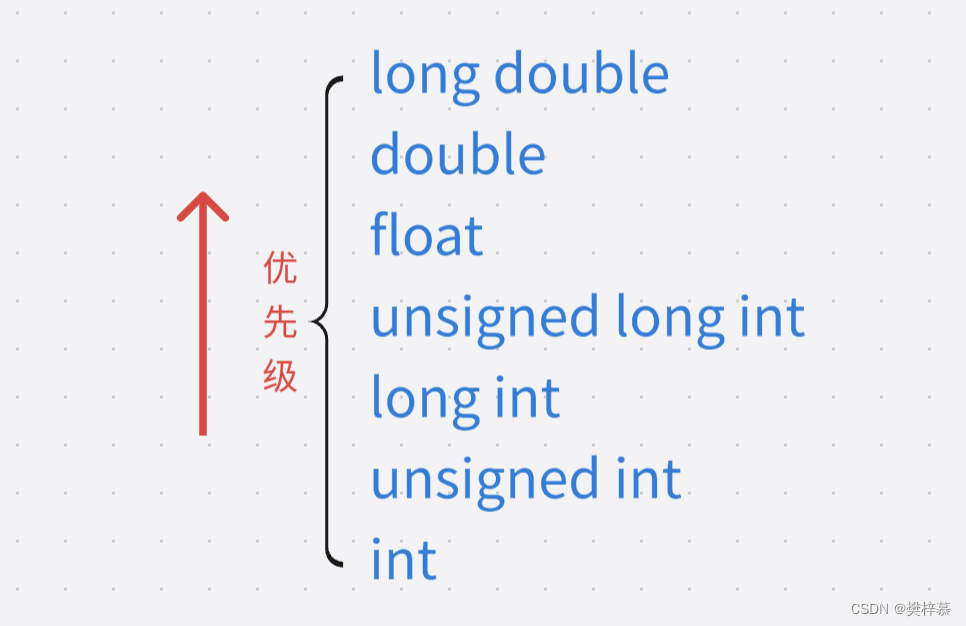
如果某个操作数的类型在上面这个列表中排名较低,那么首先要转换为另外一个操作数的类型后执行运算。
警告:
但是算术转换要合理,要不然会有一些潜在的问题,如精度丢失:
float f = 3.14;
int num = f;//隐式转换,会有精度丢失三、操作符的属性
复杂表达式的求值有三个影响的因素:
- 操作符的优先级
- 操作符的结合性
- 是否控制求值顺序
两个相邻的操作符先执行哪个?取决于他们的优先级。
如果两者的优先级相同,取决于他们的结合性。
(一)操作符优先级汇总
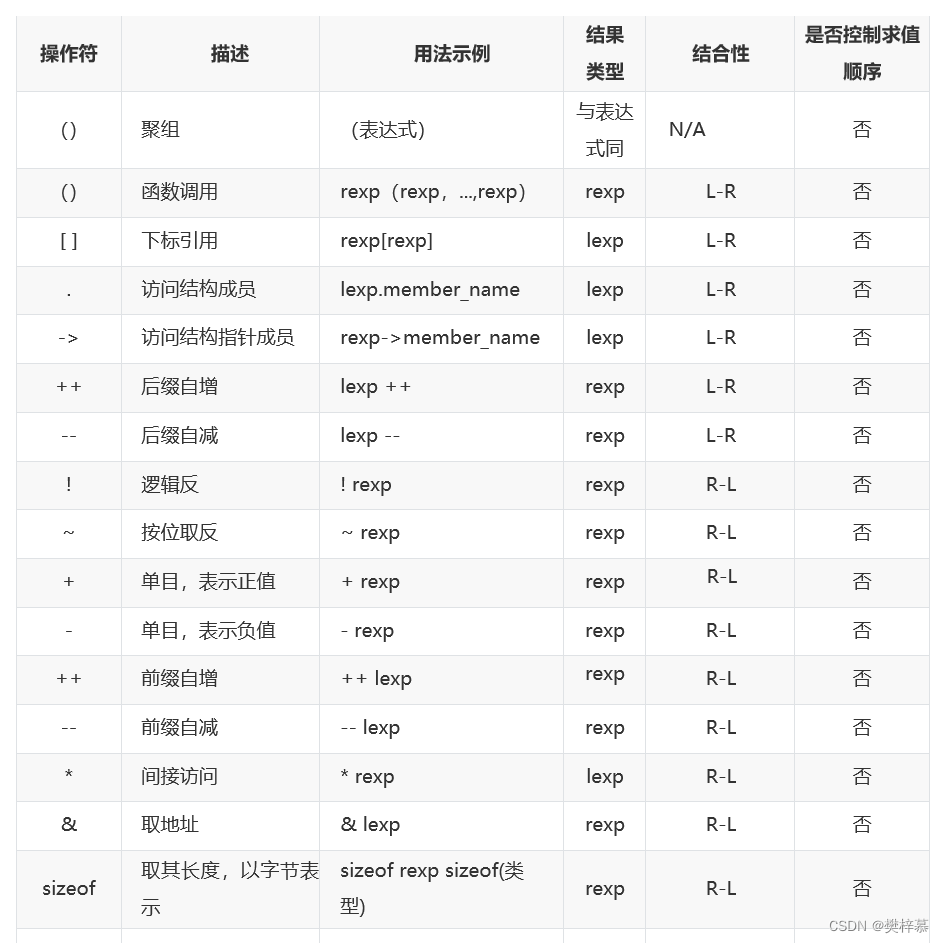
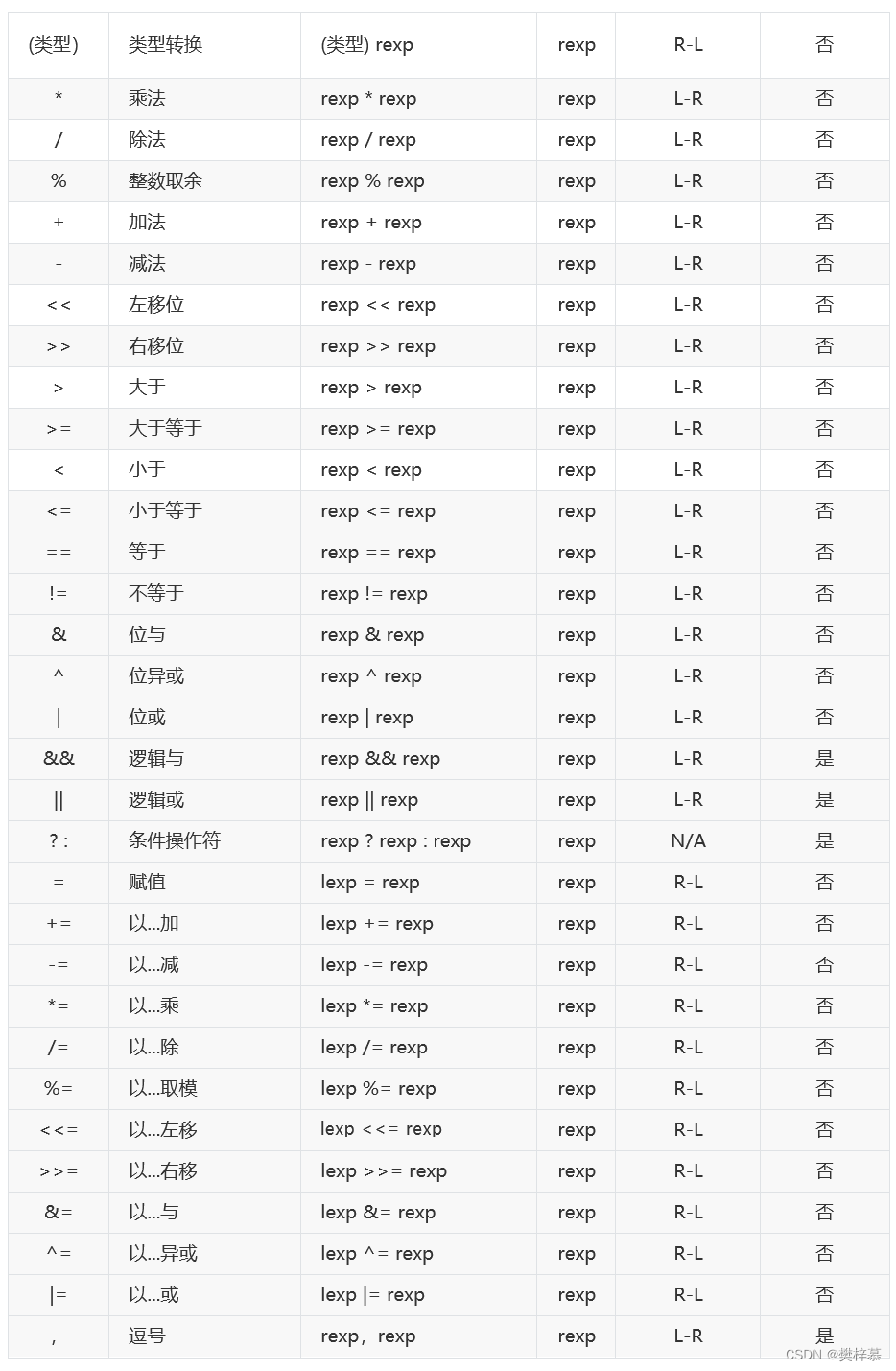
(二)一些问题表达式
//表达式的求值部分由操作符的优先级决定。
//代码1
a* b + c * d + e * f分析:代码在计算的时候,由于*比+的优先级高,只能保证,*的计算是比+早,但是优先级并不
能决定第三个*比第一个+早执行。
所以表达式的计算机顺序就可能是:
a* b
c* d
a* b + c * d
e * f
a * b + c * d + e * f
或者:
a * b
c * d
e * f
a * b + c * d
a * b + c * d + e * f
//代码2
c + --c; 分析:同上,操作符的优先级只能决定自减--的运算在+的运算的前面,但是我们并没有办法得
知,+操作符的左操作数的获取在右操作数之前还是之后求值,所以结果是不可预测的,是有歧义
的。
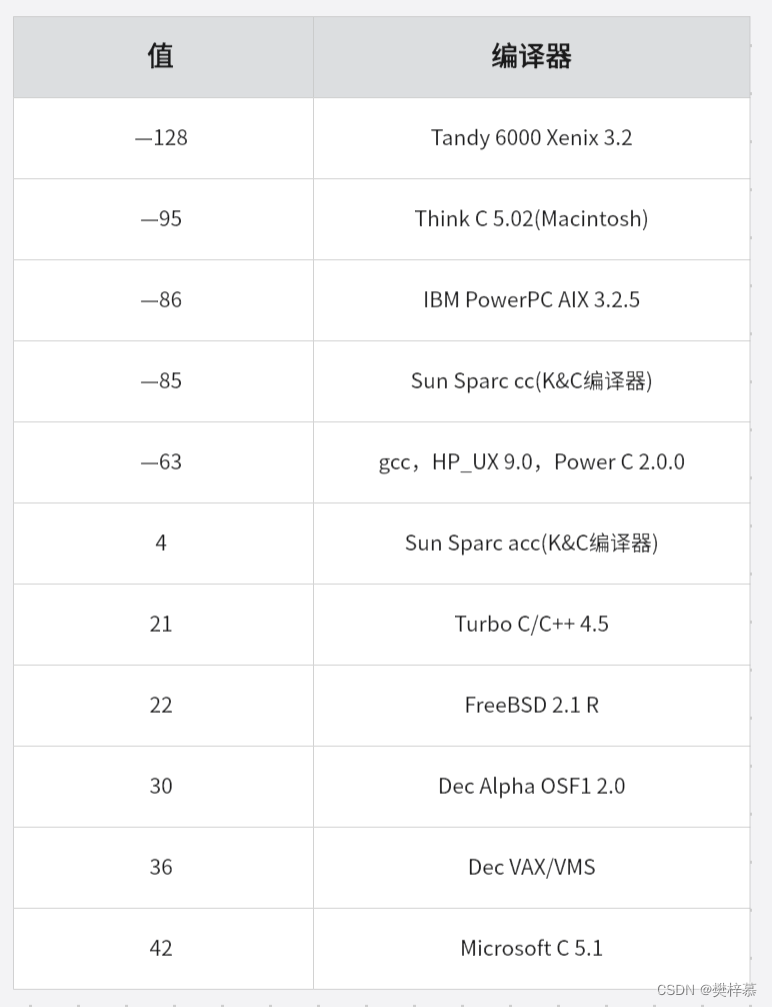
//代码3-非法表达式
int main()
{
int i = 10;
i = i-- - --i * (i = -3) * i++ + ++i;
printf("i = %d\n", i);
return 0;
}分析:同上,代码3有歧义,此时程序运算的结果就取决于编译器了。
如下图:
//代码4
int fun()
{
static int count = 1;
return ++count;
}
int main()
{
int answer;
answer = fun() - fun() * fun();
printf("%d\n", answer);//输出多少?
return 0;
}分析: answer = fun() - fun() * fun(); 中我们只能通过操作符的优先级得知:先算乘法,
再算减法。但是函数的调用先后顺序无法通过操作符的优先级确定。
//代码5
#include <stdio.h>
int main()
{
int i = 1;
int ret = (++i) + (++i) + (++i);
printf("%d\n", ret);
printf("%d\n", i);
return 0;
}分析:这段代码中的第一个 + 在执行的时候,第三个++是否执行,这个是不确定的,因为依靠操作符的优先级和结合性是无法决定第一个 + 和第三个前置 ++ 的先后顺序。
经过上面的例子,我们可以得出结论:
我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径,那这个表达式就是存在问题的,此时的结果取决于该编译器是如何编译的。
本篇文章的内容就到这里,为了防止大家以后再遇到类似表达式求值问题时出错,大家可以收藏本篇文章随时查阅操作符优先级与类型转换相关内容🍀