第二章 数据的表示和运算

一、数值与编码

1.1 进制转换

任意进制->十进制：

二进制<->八进制、十六进制：

各种进制的常见书写方式：

十进制->任意进制：（用拼凑法最快）

真值：符合人类习惯的数字（带±号的数）

机器数：正负号被“数字化”

1.2 定点数

常规计数：定点数；科学计数法：浮点数

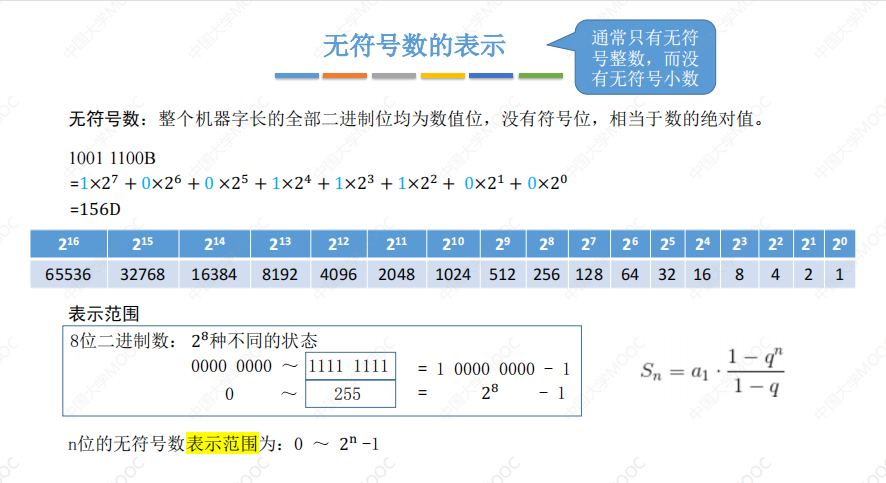
无符号数：

有符号定点数：

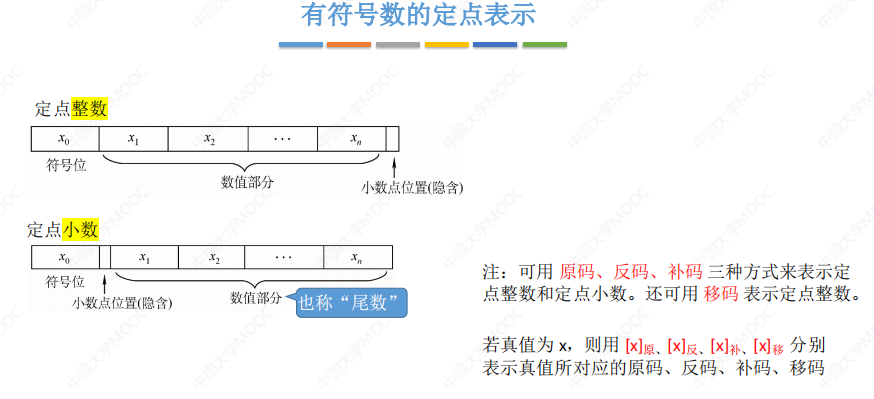
既含整数又含小数则分开表示

有符号数：

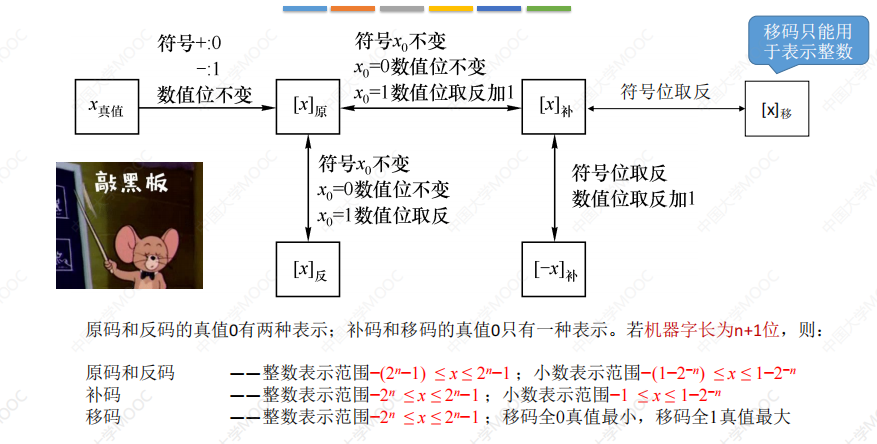
二、运算方法及运算电路

2.1 移位运算

移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。可用移位运算实现乘法、除法

原码算术移位：

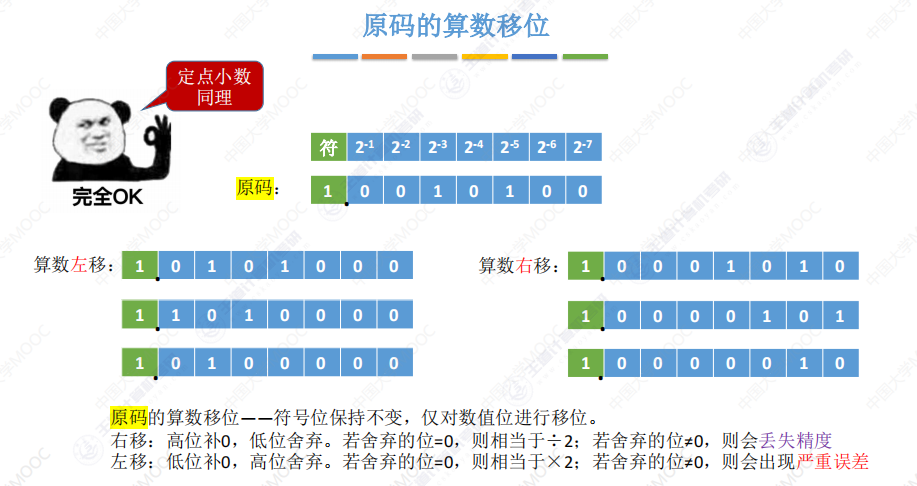
反码算术移位：

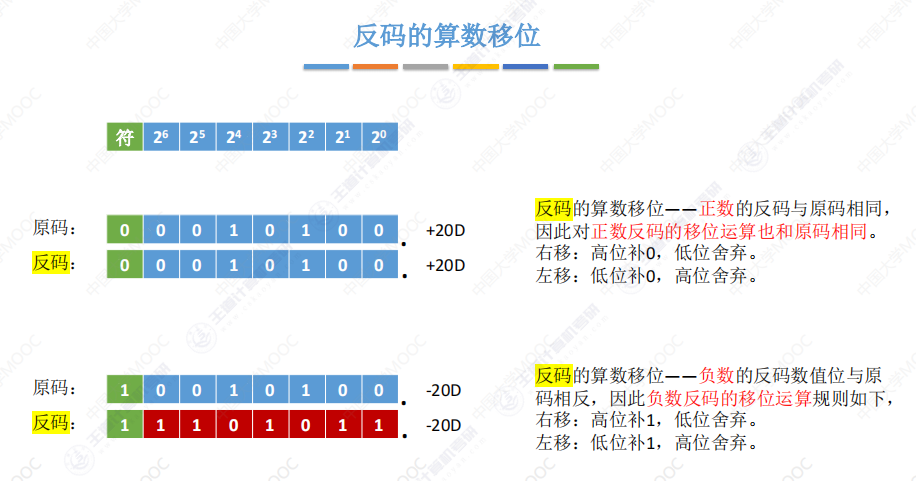
补码算术移位：

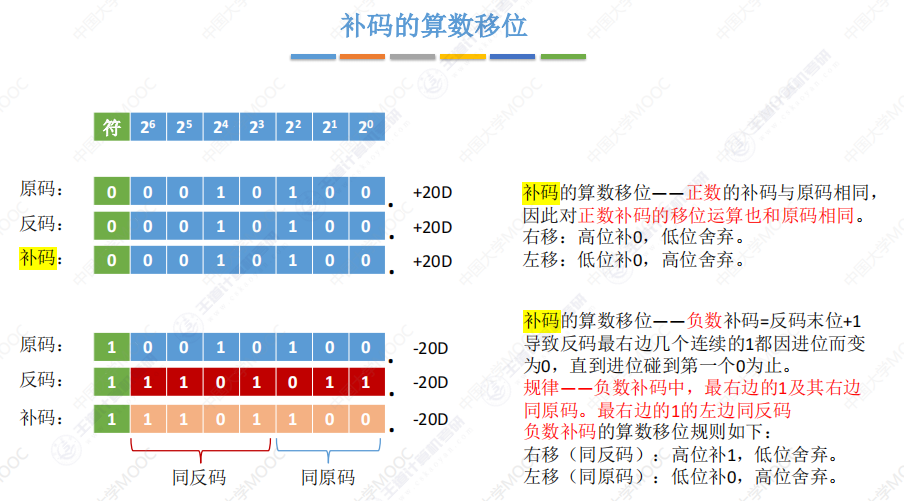
总结：

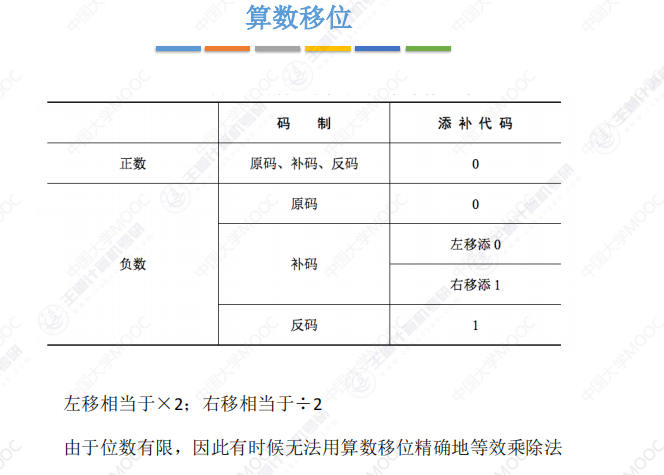
逻辑移位：

循环移位：

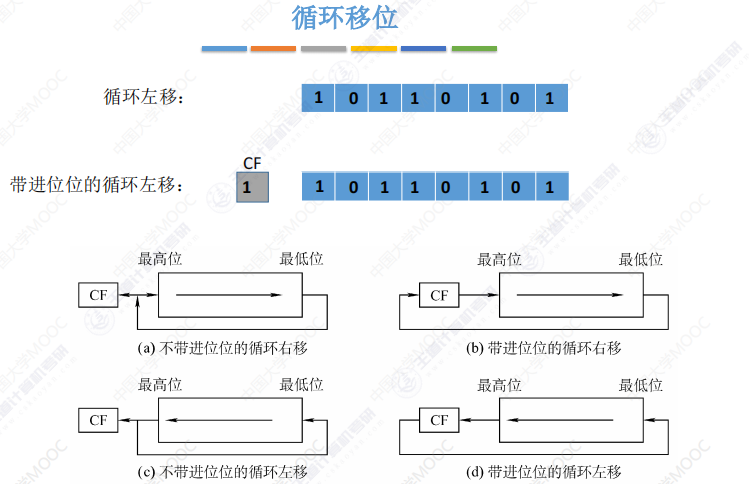
2.2 定点数加减

原码加减：

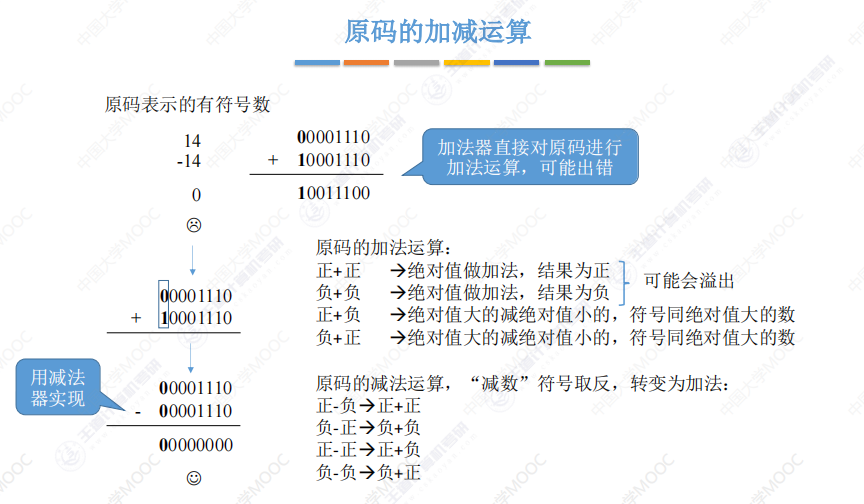
补码加减：

溢出判断（三个方法）：

只有“正数+正数”会上溢（正+正=负）

只有“负数+负数”才会下溢（负+负=正）

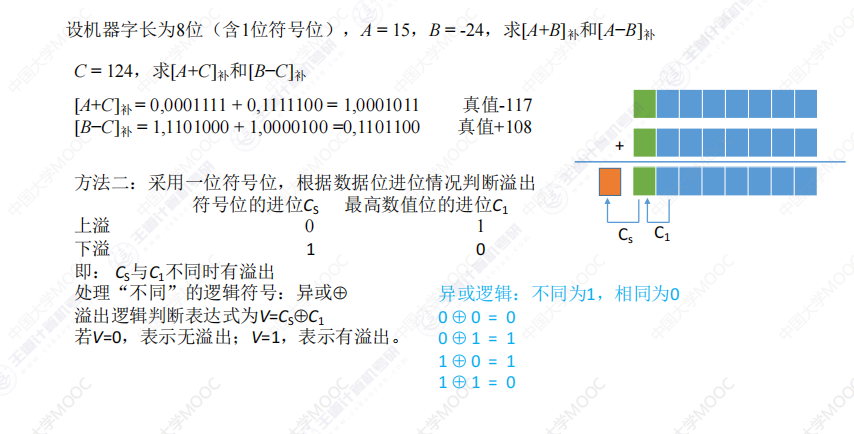
2.3 定点数原码乘法

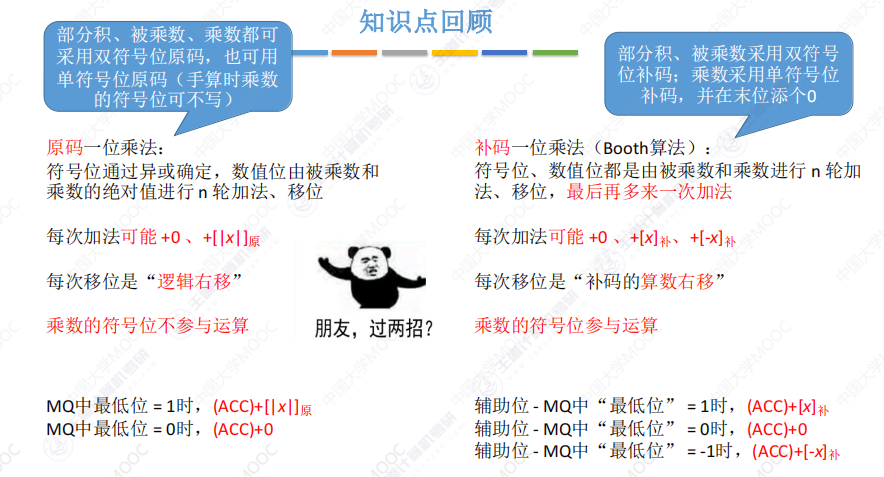
原码一位乘法：

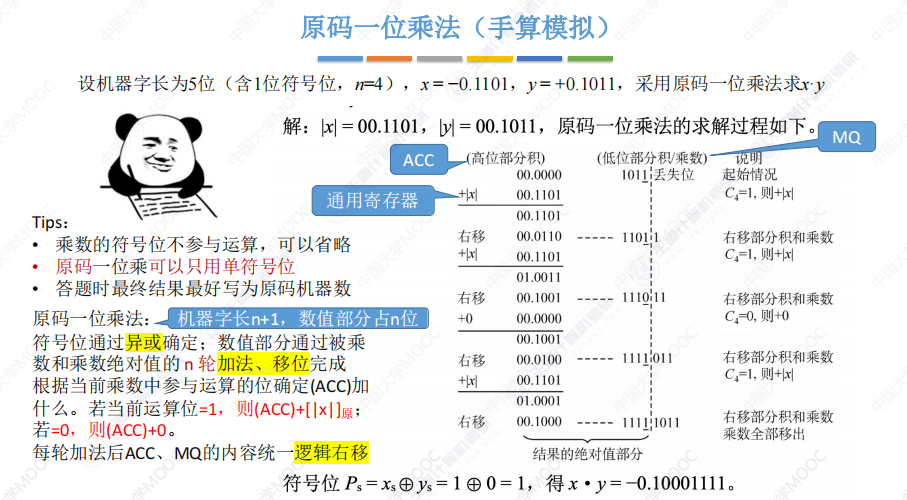
补码一位乘法（Booth算法）：

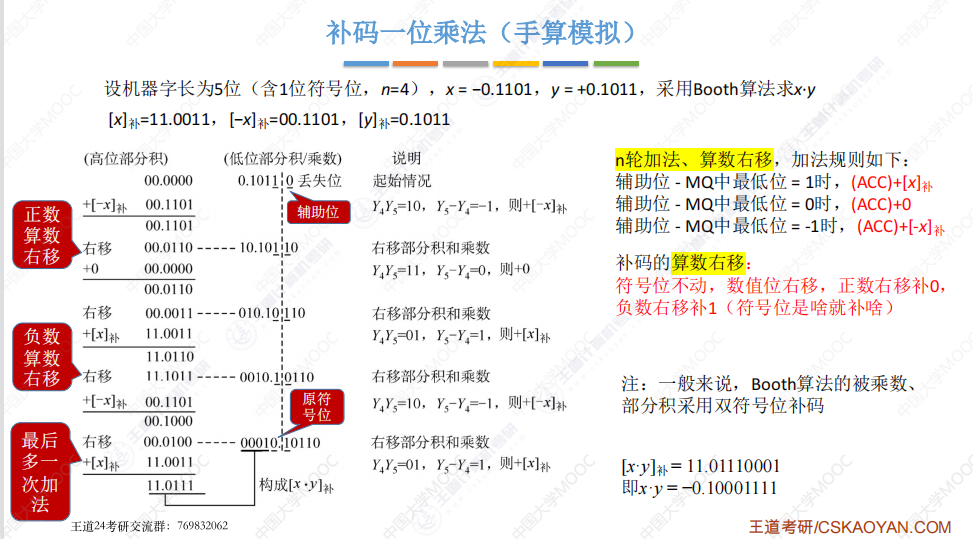
对比：

-----除法

2.4 数据的存储和排列

大小端模式：

大端：从最高有效字节到最低有效字节的顺序存储数据。小端：相反

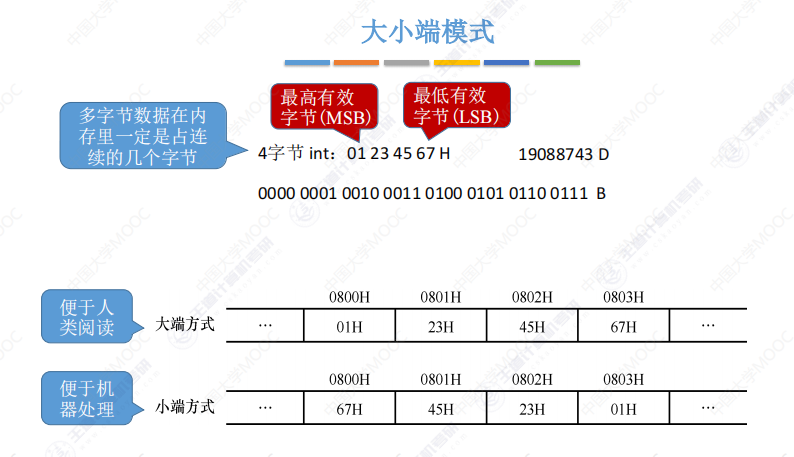
边界对齐：

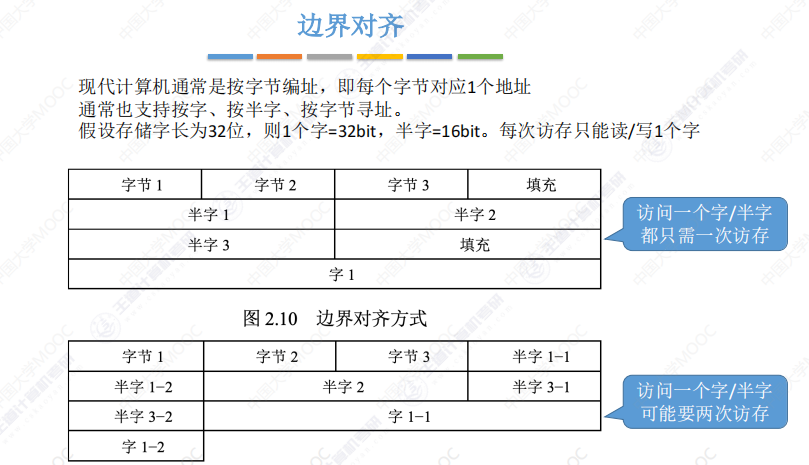
三、浮点数的表示与运算

3.1 浮点数的表示

尾数规格化：

规格化浮点数特点：

3.2 IEEE 754标准

移码的定义为：移码=真值+偏置值（移码只能用于表示整数） 偏置值一般取 2^n-1，此时移码=补码 符号位取反

然而，偏置值可以取其他值，例如2^n-1-1

三种IEEE 754标准：

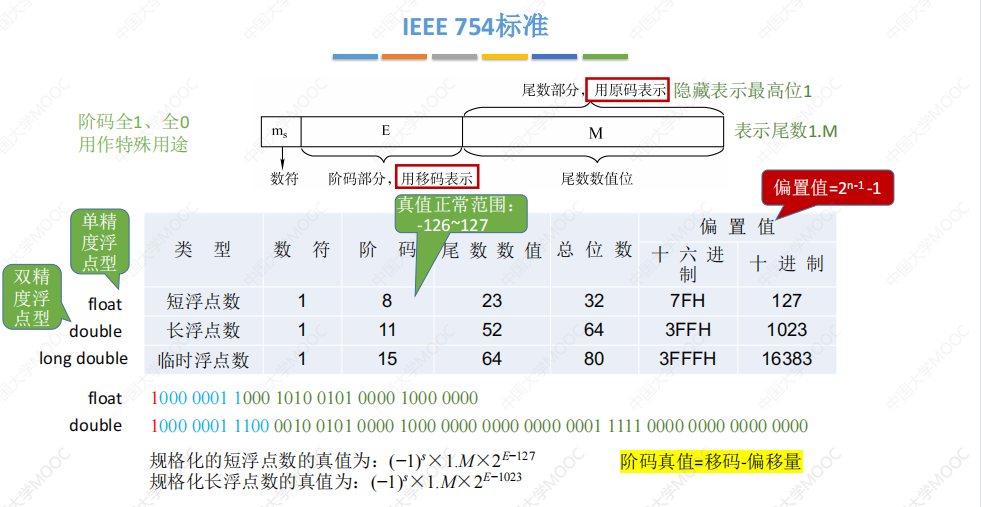
例子：

表示范围：

当要表示的数绝对值还要更小时：

3.3 浮点数加减运算

两种舍入法：

3.4 强制类型转换

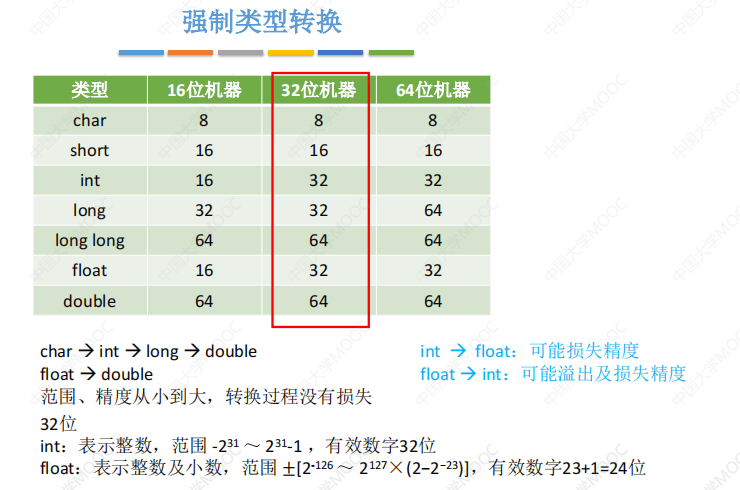
主要参考：王道考研课程
后续会持续更新考研408部分的学习笔记，欢迎关注。
github仓库（含所有相关源码）：408数据结构笔记