目录
1 问题
2 用条件期望,求合成的次数
2.1 思路1
2.2 思路2
3 用条件期望,求合成的个数
3.1 令X表示用材料1往上合成时,合成材料2的个数
3.2 令Y表示用材料1往上合成时,合成材料3的个数
4 用条件期望,求合成的材料的阶数
5 比较计算次数,个数,合成东西的阶数
1 问题
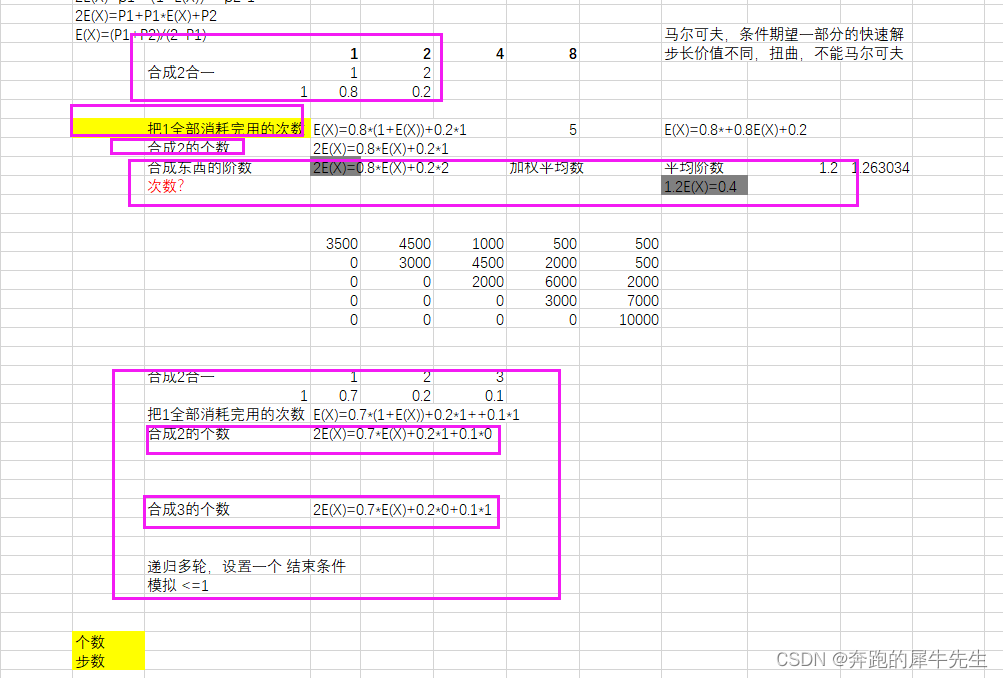
假设有如下合成问题
求1个材料1合成材料2的次数 是多少
求1个材料1合成材料2的个数是多少

2 用条件期望,求合成的次数
令X表示用材料1往上合成时,合成材料2的次数
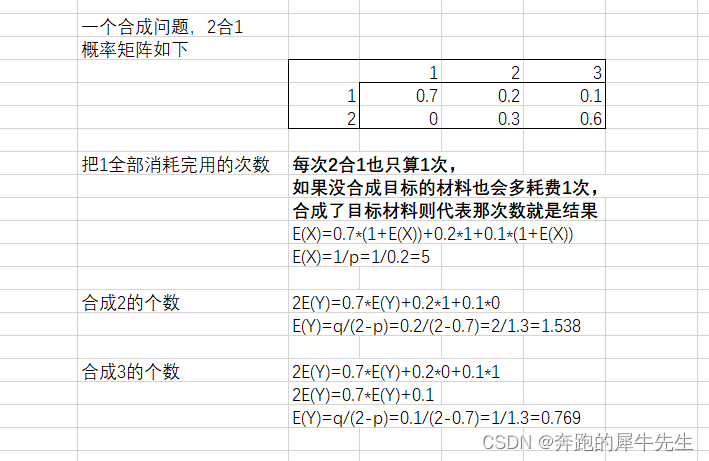
每次2合1也只算1次,,如果没合成目标的材料也会多耗费1次,,合成了目标材料则代表那次数就是结果
2.1 思路1
这里和实际的概率设计有关系,如果材料3无法合成材料2,那计算材料3递归回到材料的合成次数是没有意义的。
- E(X)=0.7*(1+E(X))+0.2*1+0.1*0
- E(X)=0.9+0.7*E(X))
- E(X)=0.9/0.3=3
- 即
- E(X)=p1*(1+E(X))+p2*1+p3*0
- E(X)=p1*p2+p1*E(X)
- E(X)=(p1+p2)/(1-p1)
2.2 思路2
这里和实际的概率设计有关系,如果材料3也可以合成材料2,即p3-->2的概率不为0,那计算材料3递归回到材料的合成次数是有意义的。
- E(X)=0.7*(1+E(X))+0.2*1+0.1*(1+E(X))
- E(X)=1/0.2=5
- 即
- E(X)=p1*(1+E(X))+p2*1+p3*(1+E(X))
- E(X)=p1+p2+p3+(p1+p3)*E(X)
- E(X)=(p1+p2+p3)/p2
- E(X)=1/p2
- 这和几何分布的求的期望次数 E(X)=1/P也是一样的,因为每次实验都是独立的
3 用条件期望,求合成的个数
3.1 令X表示用材料1往上合成时,合成材料2的个数
每次合成需要消耗2个材料1
- 2E(Y)=0.7*E(Y)+0.2*1+0.1*0
- E(Y)=0.2/(2-0.7)=2/13=0.1538
- 即
- 2E(Y)=p1*E(Y)+p2*1+p3*0
- E(Y)=p2/(2-p1)
3.2 令Y表示用材料1往上合成时,合成材料3的个数
- 2E(Y)=0.7*E(Y)+0.2*0+0.1*1
- 2E(Y)=0.7*E(Y)+0.1
- E(Y)=0.1/(2-0.7)=1/13=0.0769
- 即
- 2E(Y)=p1*E(Y)+p2*0+p3*1
- E(Y)=p3/(2-p1)
4 用条件期望,求合成的材料的阶数
- 先要考虑材料等级对应的实际权重
- 然后求加权平均值就是,这一级材料的期望生成的材料等级阶。(生成的值1.5,3等要去匹配1,2,4 而不是去匹配1,2,3等!)

5 比较计算次数,个数,合成东西的阶数
- 计算合成材料的个数,和合成公式的关系很大,几个材料1合成1个材料2呢?甚至计算过程中允许合成材料不相等, 2*材料1=材料2 , 3*材料2=材料3也是可以的。但需要调整每阶的合成公式
- 计算合成材料的次数,和选择的合成策略有一定关系,